De Wikipedia, la enciclopedia libre
En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en fenómenos reales.
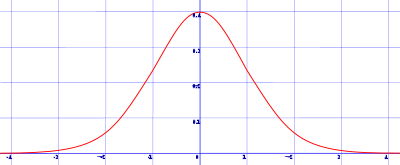
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro. Esta curva se conoce como campana de Gauss.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística es un modelo matemático que sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, cuando la distribución de la población de la cual se extrae la muestra no es normal.[1] Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una supuesta "normalidad".
En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas.

Abraham de Moivre, descubridor de la distribución normal
La distribución normal fue presentada por vez primera por Abraham de Moivre en un artículo del año 1733,[2] que fue reimpreso en la segunda edición de su The Doctrine of Chances, de 1738, en el contexto de cierta aproximación de la distribución binomial para grandes valores de n. Su resultado fue ampliado por Laplace en su libro Teoría analítica de las probabilidades (1812), y en la actualidad se llama Teorema de De Moivre-Laplace.
Laplace usó la distribución normal en el análisis de errores de experimentos. El importante método de mínimos cuadrados fue introducido por Legendre en 1805. Gauss, que afirmaba haber usado el método desde 1794, lo justificó rigurosamente en 1809 asumiendo una distribución normal de los errores. El nombre de Gauss se ha asociado a esta distribución porque la usó con profusión cuando analizaba datos astronómicos[3] y algunos autores le atribuyen un descubrimiento independiente del de De Moivre.[4] Esta atribución del nombre de la distribución a una persona distinta de su primer descubridor es un claro ejemplo de la Ley de Stigler.
El nombre de "campana" viene de Esprit Jouffret que usó el término "bell surface" (superficie campana) por primera vez en 1872 para una distribución normal bivariante de componentes independientes. El nombre de "distribución normal" fue otorgado independientemente por Charles S. Peirce, Francis Galton y Wilhelm Lexis hacia 1875.[cita requerida] A pesar de esta terminología, otras distribuciones de probabilidad podrían ser más apropiadas en determinados contextos; véase la discusión sobre ocurrencia, más abajo.
[editar] Definición formal
Hay varios modos de definir formalmente una distribución de probabilidad. La forma más visual es mediante su función de densidad. De forma equivalente, también pueden darse para su definición la función de distribución, los momentos, la función característica y la función generatriz de momentos, entre otros.
[editar] Función de densidad
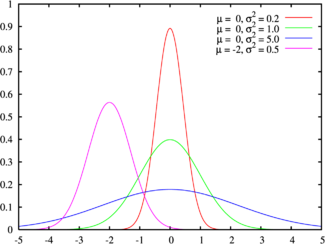
Se dice que una variable aleatoria continua X sigue una distribución normal de parámetros μ y σ y se denota X~N(μ, σ) si su función de densidad está dada por:
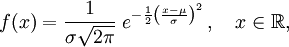
donde μ (mu) es la media y σ (sigma) es la desviación típica (σ2 es la varianza).[5]
Se llama distribución normal "estándar" a aquélla en la que sus parámetros toman los valores μ = 0 y σ = 1. En este caso la función de densidad tiene la siguiente expresión:
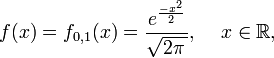
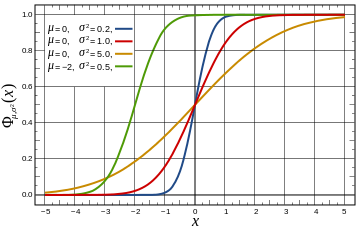
Su gráfica se muestra a la derecha y con frecuencia se usan tablas para el cálculo de los valores de su distribución.
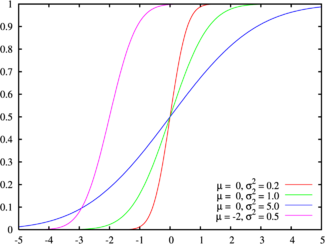
[editar] Función de distribución
La función de distribución de la distribución normal está definida como sigue:
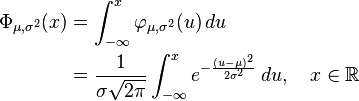
Por tanto, la función de distribución de la normal estándar es:
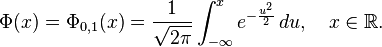
Esta función de distribución puede expresarse en términos de una función especial llamada función error de la siguiente forma:
![Phi(x) =frac{1}{2} Bigl[ 1 + operatorname{erf} Bigl( frac{x}{sqrt{2}} Bigr) Bigr], quad xinmathbb{R},](https://petalofucsia.blogia.com/upload/externo-9121802473a43886e7e45fdd9f943fbe.png)
y la propia función de distribución puede, por consiguiente, expresarse así:
![Phi_{mu,sigma^2}(x) =frac{1}{2} Bigl[ 1 + operatorname{erf} Bigl( frac{x-mu}{sigmasqrt{2}} Bigr) Bigr], quad xinmathbb{R}.](https://petalofucsia.blogia.com/upload/externo-da500c9272562208ae0fbbac30128df9.png)
El complemento de la función de distribución de la normal estándar, 1 − Φ(x), se denota con frecuencia Q(x), y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.[6] [7] Esto representa la cola de probabilidad de la distribución gaussiana. También se usan ocasionalmente otras definiciones de la función Q, las cuales son todas ellas transformaciones simples de Φ.[8]
La inversa de la función de distribución de la normal estándar (función cuantil) puede expresarse en términos de la inversa de la función de error:
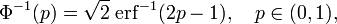
y la inversa de la función de distribución puede, por consiguiente, expresarse como:
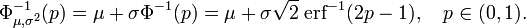
Esta función cuantil se llama a veces la función probit. No hay una primitiva elemental para la función probit. Esto no quiere decir meramente que no se conoce, sino que se ha probado la inexistencia de tal función. Existen varios métodos exactos para aproximar la función cuantil mediante la distribución normal (véase función cuantil).
Los valores Φ(x) pueden aproximarse con mucha precisión por distintos métodos, tales como integración numérica, series de Taylor, series asintóticas y fracciones continuas.
[editar] Límite inferior y superior estrictos para la función de distribución
Para grandes valores de x la función de distribución de la normal estándar 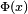 es muy próxima a 1 y
es muy próxima a 1 y 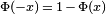 está muy cerca de 0. Los límites elementales
está muy cerca de 0. Los límites elementales
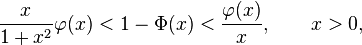
en términos de la densidad  son útiles.
son útiles.
Usando el cambio de variable v = u²/2, el límite superior se obtiene como sigue:
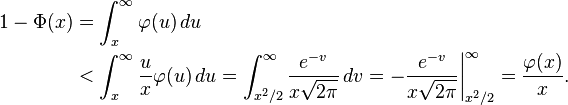
De forma similar, usando 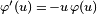 y la regla del cociente,
y la regla del cociente,
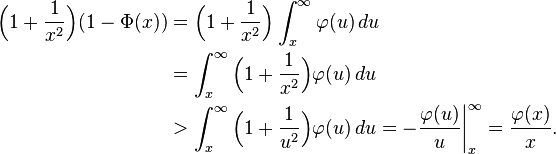
Resolviendo para 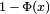 proporciona el límite inferior.
proporciona el límite inferior.
[editar] Funciones generadoras
[editar] Función generadora de momentos
La función generadora de momentos se define como la esperanza de e(tX). Para una distribución normal, la función generadora de momentos es:
![M_X(t) = mathrm{E} left[ e^{tX} right] = int_{-infty}^{infty} frac{1}{sigma sqrt{2pi} } e^{-frac{(x - mu)^2}{2 sigma^2}} e^{tx} , dx = e^{mu t + frac{sigma^2 t^2}{2}}](https://petalofucsia.blogia.com/upload/externo-59ef7a28f5657844fd57dce74a826b25.png)
como puede comprobarse completando el cuadrado en el exponente.
[editar] Función característica
La función característica se define como la esperanza de eitX, donde i es la unidad imaginaria. De este modo, la función característica se obtiene reemplazando t por it en la función generadora de momentos.
Para una distribución normal, la función característica es[9]
![begin{align} chi_X(t;mu,sigma) &{} = M_X(i t) = mathrm{E} left[ e^{i t X} right] &{}= int_{-infty}^{infty} frac{1}{sigma sqrt{2pi}} e^{- frac{(x - mu)^2}{2sigma^2}} e^{i t x} , dx &{}= e^{i mu t - frac{sigma^2 t^2}{2}} end{align}](https://petalofucsia.blogia.com/upload/externo-4d61a4ac57cb1529ad0d807e2c3a971e.png)
[editar] Propiedades
Algunas propiedades de la distribución normal son:
- Es simétrica respecto de su media, μ;
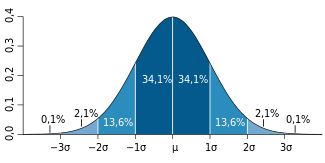
Distribución de probabilidad alrededor de la media en una distribución N(
μ,
σ).
- La moda y la mediana son ambas iguales a la media, μ;
- Los puntos de inflexión de la curva se dan para x = μ − σ y x = μ + σ.
- Distribución de probabilidad en un entorno de la media:
- en el intervalo [μ - σ, μ + σ] se encuentra comprendida, aproximadamente, el 68,26% de la distribución;
- en el intervalo [μ - 2σ, μ + 2σ] se encuentra, aproximadamente, el 95,44% de la distribución;
- por su parte, en el intervalo [μ -3σ, μ + 3σ] se encuentra comprendida, aproximadamente, el 99,74% de la distribución. Estas propiedades son de gran utilidad para el establecimiento de intervalos de confianza. Por otra parte, el hecho de que prácticamente la totalidad de la distribución se encuentre a tres desviaciones típicas de la media justifica los límites de las tablas empleadas habitualmente en la normal estándar.
- Si X ~ N(μ, σ2) y a y b son números reales, entonces (aX + b) ~ N(aμ+b, a2σ2).
- Si X ~ N(μx, σx2) e Y ~ N(μy, σy2) son variables aleatorias normales independientes, entonces:
- Su suma está normalmente distribuida con U = X + Y ~ N(μx + μy, σx2 + σy2) (demostración). Recíprocamente, si dos variables aleatorias independientes tienen una suma normalmente distribuida, deben ser normales (Teorema de Crámer).
- Su diferencia está normalmente distribuida con
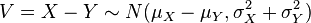 .
. - Si las varianzas de X e Y son iguales, entonces U y V son independientes entre sí.
- La divergencia de Kullback-Leibler,
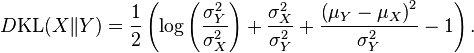
- Si
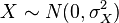 e
e 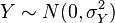 son variables aleatorias independientes normalmente distribuidas, entonces:
son variables aleatorias independientes normalmente distribuidas, entonces: - Si
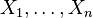 son variables normales estándar independientes, entonces
son variables normales estándar independientes, entonces 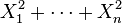 sigue una distribución χ² con n grados de libertad.
sigue una distribución χ² con n grados de libertad. - Si
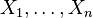 son variables normales estándar independientes, entonces la media muestral
son variables normales estándar independientes, entonces la media muestral 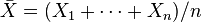 y la varianza muestral
y la varianza muestral 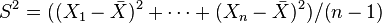 son independientes. Esta propiedad caracteriza a las distribuciones normales y contribuye a explicar por qué el test-F no es robusto respecto a la no-normalidad).
son independientes. Esta propiedad caracteriza a las distribuciones normales y contribuye a explicar por qué el test-F no es robusto respecto a la no-normalidad).
[editar] Estandarización de variables aleatorias normales
Como consecuencia de la Propiedad 1; es posible relacionar todas las variables aleatorias normales con la distribución normal estándar.
Si X ~ N(μ,σ2), entonces
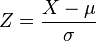
es una variable aleatoria normal estándar: Z ~ N(0,1).
La transformación de una distribución X ~ N(μ, σ) en una N(0, 1) se llama normalización, estandarización o tipificación de la variable X.
Una consecuencia importante de esto es que la función de distribución de una distribución normal es, por consiguiente,
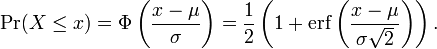
A la inversa, si Z es una distribución normal estándar, Z ~ N(0,1), entonces
X = σZ + μes una variable aleatoria normal tipificada de media μ y varianza σ2.
La distribución normal estándar está tabulada (habitualmente en la forma de el valor de la función de distribución Φ) y las otras distribuciones normales pueden obtenerse como transformaciones simples, como se describe más arriba, de la distribución estándar. De este modo se pueden usar los valores tabulados de la función de distribución normal estándar para encontrar valores de la función de distribución de cualquier otra distribución normal.
Los primeros momentos de la distribución normal son:
| Número | Momento | Momento central | Cumulante |
|---|
| 0 | 1 | 1 | |
| 1 | μ | 0 | μ |
| 2 | μ2 + σ2 | σ2 | σ2 |
| 3 | μ3 + 3μσ2 | 0 | 0 |
| 4 | μ4 + 6μ2σ2 + 3σ4 | 3σ4 | 0 |
| 5 | μ5 + 10μ3σ2 + 15μσ4 | 0 | 0 |
| 6 | μ6 + 15μ4σ2 + 45μ2σ4 + 15σ6 | 15σ6 | 0 |
| 7 | μ7 + 21μ5σ2 + 105μ3σ4 + 105μσ6 | 0 | 0 |
| 8 | μ8 + 28μ6σ2 + 210μ4σ4 + 420μ2σ6 + 105σ8 | 105σ8 | 0 |
Todos los cumulantes de la distribución normal, más allá del segundo, son cero.
Los momentos centrales de orden superior (2k con μ = 0) vienen dados por la fórmula
![Eleft[X^{2k}right]=frac{(2k)!}{2^k k!} sigma^{2k}.](https://petalofucsia.blogia.com/upload/externo-ecd1b3e124ecd1cab539b6ac0cb45ed2.png)
[editar] El Teorema del Límite Central
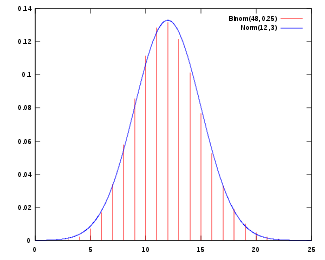
Gráfica de la función de distribución de una normal con μ = 12 y σ = 3, aproximando la función de distribución de una
binomial con
n = 48 y
p = 1/4
El Teorema del límite central establece que bajo ciertas condiciones (como pueden ser independientes e idénticamente distribuidas con varianza finita), la suma de un gran número de variables aleatorias se distribuye aproximadamente como una normal.
La importancia práctica del Teorema del límite central es que la función de distribución de la normal puede usarse como aproximación de algunas otras funciones de distribución. Por ejemplo:
- Una distribución binomial de parámetros n y p es aproximadamente normal para grandes valores de n, y p no demasiado cercano a 1 ó 0 (algunos libros recomiendan usar esta aproximación sólo si np y n(1 − p) son ambos, al menos, 5; en este caso se debería aplicar una corrección de continuidad).
La normal aproximada tiene parámetros μ = np, σ2 = np(1 − p).
- Una distribución de Poisson con parámetro λ es aproximadamente normal para grandes valores de λ.
La distribución normal aproximada tiene parámetros μ = σ2 = λ.
La exactitud de estas aproximaciones depende del propósito para el que se necesiten y de la tasa de convergencia a la distribución normal. Se da el caso típico de que tales aproximaciones son menos precisas en las colas de la distribución. El Teorema de Berry-Esséen proporciona un límite superior general del error de aproximación de la función de distribución.
[editar] Divisibilidad infinita
Las normales tienen una distribución de probabilidad infinitamente divisible: dada una media μ, una varianza σ 2 ≥ 0, y un número natural n, la suma X1 + . . . + Xn de n variables aleatorias independientes

tiene esta específica distribución normal (para verificarlo, úsese la función característica de convolución y la inducción matemática).
[editar] Estabilidad
Las distribuciones normales son estrictamente estables.
[editar] Desviación típica e intervalos de confianza
Alrededor del 68% de los valores de una distribución normal están a una distancia σ > 1 (desviación típica) de la media, μ; alrededor del 95% de los valores están a dos desviaciones típicas de la media y alrededor del 99,7% están a tres desviaciones típicas de la media. Esto se conoce como la "regla 68-95-99,7" o la "regla empírica".
Para ser más precisos, el área bajo la curva campana entre μ − nσ y μ + nσ en términos de la función de distribución normal viene dada por
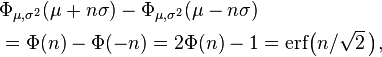
donde erf es la función error. Con 12 decimales, los valores para los puntos 1-, 2-, hasta 6-σ son:
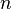 | 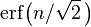 |
|---|
| 1 | 0,682689492137 |
| 2 | 0,954499736104 |
| 3 | 0,997300203937 |
| 4 | 0,999936657516 |
| 5 | 0,999999426697 |
| 6 | 0,999999998027 |
La siguiente tabla proporciona la relación inversa de múltiples σ correspondientes a unos pocos valores usados con frecuencia para el área bajo la campana de Gauss. Estos valores son útiles para determinar intervalos de confianza para los niveles especificados basados en una curva normalmente distribuida (o estimadores asintóticamente normales):
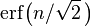 |  |
|---|
| 0,80 | 1,28155 |
| 0,90 | 1,64485 |
| 0,95 | 1,95996 |
| 0,98 | 2,32635 |
| 0,99 | 2,57583 |
| 0,995 | 2,80703 |
| 0,998 | 3,09023 |
| 0,999 | 3,29052 |
| 0,9999 | 3,8906 |
| 0,99999 | 4,4172 |
donde el valor a la izquierda de la tabla es la proporción de valores que caerán en el intervalo dado y n es un múltiplo de la desviación típica que determina la anchura de el intervalo.
[editar] Forma familia exponencial
La distribución normal tiene forma de familia exponencial biparamétrica con dos parámetros naturales, μ y 1/σ2, y estadísticos naturales X y X2. La forma canónica tiene como parámetros 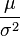 y
y 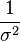 y estadísticos suficientes
y estadísticos suficientes 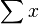 y
y 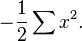
[editar] Distribución normal compleja
Considérese la variable aleatoria compleja gaussiana
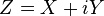
donde X e Y son variables gaussianas reales e independientes con igual varianza 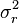 . La función de distribución de la variable conjunta es entonces
. La función de distribución de la variable conjunta es entonces
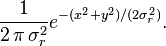
Como 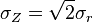 , la función de distribución resultante para la variable gaussiana compleja Z es
, la función de distribución resultante para la variable gaussiana compleja Z es
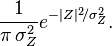
[editar] Distribuciones relacionadas
- Y˜Cauchy(μ = 0,θ = 1) es una distribución de Cauchy si Y = X1 / X2 para X1˜N(0,1) y X2˜N(0,1) son dos distribuciones normales independientes.
- Distribución normal truncada. si
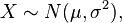 entonces truncando X por debajo de A y por encima de B dará lugar a una variable aleatoria de media
entonces truncando X por debajo de A y por encima de B dará lugar a una variable aleatoria de media 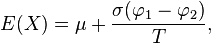 donde
donde 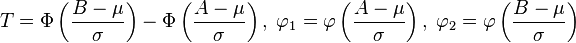 y
y 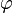 es la función de densidad de una variable normal estándar.
es la función de densidad de una variable normal estándar.
[editar] Estadística descriptiva e inferencial
[editar] Resultados
De la distribución normal se derivan muchos resultados, incluyendo rangos de percentiles ("percentiles" o "cuantiles"), curvas normales equivalentes, stanines, z-scores, y T-scores. Además, un número de procedimientos de estadísticos de comportamiento están basados en la asunción de que esos resultados están normalmente distribuidos. Por ejemplo, el test de Student y el análisis de varianza (ANOVA) (véase más abajo). La gradación de la curva campana asigna grados relativos basados en una distribución normal de resultados.
[editar] Tests de normalidad
Los tests de normalidad se aplican a conjuntos de datos para determinar su similitud con una distribución normal. La hipótesis nula es, en estos casos, si el conjunto de datos es similar a una distribución normal, por lo que un P-valor suficientemente pequeño indica datos no normales.
[editar] Estimación de parámetros
[editar] Estimación de parámetros de máxima verosimilitud
Supóngase que
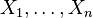
son independientes y cada una está normalmente distribuida con media μ y varianza σ 2 > 0. En términos estadísticos los valores observados de estas n variables aleatorias constituyen una "muestra de tamaño n de una población normalmente distribuida. Se desea estimar la media poblacional μ y la desviación típica poblacional σ, basándose en las valores observados de esta muestra. La función de densidad conjunta de estas n variables aleatorias independientes es
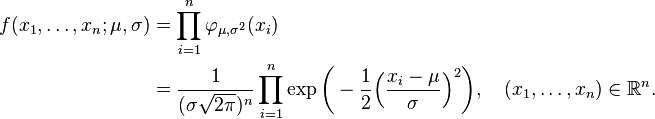
Como función de μ y σ, la función de verosimilitud basada en las observaciones X1, ..., Xn es
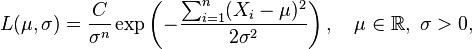
con alguna constante C > 0 (de la cual, en general, se permitiría incluso que dependiera de X1, ..., Xn, aunque desapareciera con las derivadas parciales de la función de log-verosimilitud respecto a los parámetros tenidos en cuenta, véase más abajo).
En el método de máxima verosimilitud, los valores de μ y σ que maximizan la función de verosimilitud se toman como estimadores de los parámetros poblacionales μ y σ.
Habitualmente en la maximización de una función de dos variables, se podrían considerar derivadas parciales. Pero aquí se explota el hecho de que el valor de μ que maximiza la función de verosimilitud con σ fijo no depende de σ. No obstante, encontramos que ese valor de μ, entonces se sustituye por μ en la función de verosimilitud y finalmente encontramos el valor de σ que maximiza la expresión resultante.
Es evidente que la función de verosimilitud es una función decreciente de la suma
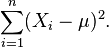
Así que se desea el valor de μ que minimiza esta suma. Sea
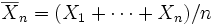
la media muestral basada en las n observaciones. Nótese que
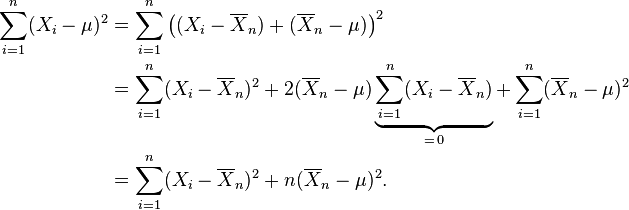
Sólo el último término depende de μ y se minimiza por
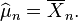
Esta es la estimación de máxima verosimilitud de μ basada en las n observaciones X1, ..., Xn. Cuando sustituimos esta estimación por μ en la función de verosimilitud, obtenemos
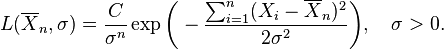
Se conviene en denotar la "log-función de verosimilitud", esto es, el logaritmo de la función de verosimilitud, con una minúscula ℓ, y tenemos
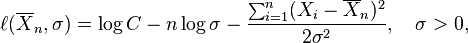
entonces
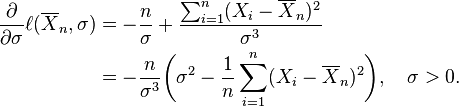
Esta derivada es positiva, cero o negativa según σ2 esté entre 0 y
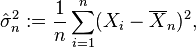
o sea igual a esa cantidad, o mayor que esa cantidad. (Si hay solamente una observación, lo que significa que n = 1, o si X1 = ... = Xn, lo cual sólo ocurre con probabilidad cero, entonces 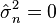 por esta fórmula, refleja el hecho de que en estos casos la función de verosimilitud es ilimitada cuando σ decrece hasta cero.)
por esta fórmula, refleja el hecho de que en estos casos la función de verosimilitud es ilimitada cuando σ decrece hasta cero.)
Consecuentemente esta media de cuadrados de residuos es el estimador de máxima verosimilitud de σ2, y su raíz cuadrada es el estimador de máxima verosimilitud de σ basado en las n observaciones. Este estimador 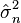 es sesgado, pero tiene un menor error medio al cuadrado que el habitual estimador insesgado, que es n/(n − 1) veces este estimador.
es sesgado, pero tiene un menor error medio al cuadrado que el habitual estimador insesgado, que es n/(n − 1) veces este estimador.
[editar] Sorprendente generalización
La derivada del estimador de máxima verosimilitud de la matriz de covarianza de una distribución normal multivariante es despreciable. Involucra el teorema espectral y la razón por la que puede ser mejor para ver un escalar como la traza de una matriz 1×1 matrix que como un mero escalar. Véase estimación de la covarianza de matrices.
[editar] Estimación insesgada de parámetros
El estimador 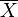 de máxima verosimilitud de la media poblacional μ, es un estimador insesgado de la media poblacional.
de máxima verosimilitud de la media poblacional μ, es un estimador insesgado de la media poblacional.
El estimador de máxima verosimilitud de la varianza es insesgado si asumimos que la media de la población es conocida a priori, pero en la práctica esto no ocurre. Cuando disponemos de una muestra y no sabemos nada de la media o la varianza de la población de la que se ha extraído, como se asumía en la derivada de máxima verosimilitud de arriba, entonces el estimador de máxima verosimilitud de la varianza es sesgado. Un estimador insesgado de la varianza σ2 es la cuasi varianza muestral:
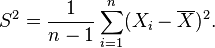
que sigue una distribución Gamma cuando las Xi son normales independientes e idénticamente distribuidas:
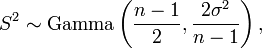
con media 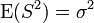 y varianza
y varianza 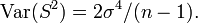
La estimación de máxima verosimilitud de la desviación típica es la raíz cuadrada de la estimación de máxima verosimilitud de la varianza. No obstante, ni ésta, ni la raíz cuadrada de la cuasivarianza muestral proporcionan un estimador insesgado para la desviación típica (véase estimación insesgada de la desviación típica para una fórmula particular para la distribución normal.
[editar] Incidencia
Las distribuciones aproximadamente normales aparecen por doquier, como queda explicado por el teorema central del límite. Cuando en un fenómeno se sospecha la presencia de un gran número de pequeñas causas actuando de forma aditiva e independiente es razonable pensar que las observaciones serán "normales". Hay métodos estadísticos para probar empíricamente esta asunción, por ejemplo, el test de Kolmogorov-Smirnov.
Hay causas que pueden actuar de forma multiplicativa (más que aditiva). En este caso, la asunción de normalidad no está justificada y es el logaritmo de la variable en cuestión el que estaría normalmente distribuido. La distribución de las variables directamente observadas en este caso se denomina log-normal.
Finalmente, si hay una simple influencia externa que tiene un gran efecto en la variable en consideración, la asunción de normalidad no está tampoco justificada. Esto es cierto incluso si, cuando la variable externa se mantiene constante, las distribuciones marginales resultantes son, en efecto, normales. La distribución completa será una superposición de variables normales, que no es en general normal. Ello está relacionado con la teoría de errores (véase más abajo).
A continuación se muestran una lista de situaciones que estarían, aproximadamente, normalmente distribuidas. Más abajo puede encontrarse una discusión detallada de cada una de ellas:
- En problemas de recuento, donde el teorema central del límite incluye una aproximación de discreta a continua y donde las distribuciones infinitamente divisibles y descomponibles están involucradas, tales como:
- En medidas fisiológicas de especímenes biológicos:
- El logaritmo de las medidas del tamaño de tejidos vivos (longitud, altura, superficie de piel, peso);
- La longitud de apéndices inertes (pelo, garras, rabos, dientes) de especímenes biológicos en la dirección del crecimento;
- Otras medidas fisiológicas podrían estar normalmente distribuidas, aunque no hay razón para esperarlo a priori;
- Se asume con frecuencia que los errores de medida están normalmente distribuidos y cualquier desviación de la normalidad se considera una cuestión que debería explicarse;
- Variables financieras, en el modelo Black-Scholes:
- Cambios en el logaritmo de
Cambios en el logaritmo de tasas de cambio, índices de precios, índices de existencias de mercado; estas variables se comportan como el interés compuesto, no como el interés simple, por tanto, son multiplicativas;
- Mientras que el modelo Black-Scholes presupone normalidad, en realidad estas variables exhiben colas pesadas, como puede verse en crash de las existencias de mercado;
- Otras variables financieras podrían estar normalmente distribuidas, pero no hay razón para esperarlo a priori;
- Intensidad de la luz:
- La intensidad de la luz láser está normalmente distribuida;
- La luz térmica tiene una distribución de Bose-Einstein en escalas de tiempo muy breves y una distribución normal en grandes escalas de tiempo debido al teorema central del límite.
Es relevante para la biolgía y la economía el hecho de que los sistemas complejos tienden a mostrar la ley de potencias más que normal.
[editar] Recuento de fotones
La intensidad de la luz de una sola fuente varía con el tiempo, así como las fluctuaciones térmicas que pueden observarse si la luz se analiza a una resolución suficientemente alta. La mecánica cuántica interpreta las medidas de la intensidad de la luz como un recuento de fotones, donde la asunción natural es usar la distribución de Poisson. Cuando la intensidad de la luz se integra a lo largo de grandes periodos de tiempo mayores que el tiempo de coherencia, la aproximación Poisson - Normal es apropiada.
[editar] Medida de errores
La normalidad es la asunción central de la teoría matemática de errores. De forma similar en el ajuste de modelos estadístico, un indicador de la bondad del ajuste es que el error residual (así es como se llaman los errores en esta circunstancia) sea independiente y normalmente distribuido. La asunción es que cualquier desviación de la normalidad necesita ser explicada. En ese sentido, en ambos, ajuste de modelos y teoría de errores, la normalidad es la única observación que no necesita ser explicada, sino que es esperada. No obstante, si los datos originales no están normalmente distribuidos (por ejemplo, si siguen una distribución de Cauchy, entonces los residuos tampoco estarán normalmente distribuidos. Este hecho es ignorado habitualmente en la práctica.
Las medidas repetidas de la misma cantidad se espera que cedan el paso a resultados que están agrupados entorno a un valor particular. Si todas las fuentes principales de errores se han tomado en cuenta, se asume que el error que queda debe ser el resultado de un gran número de muy pequeños y aditivos efectos y, por consiguiente, normal. Las desviaciones de la normalidad se interpretan como indicaciones de errores sistemáticos que no han sido tomados en cuenta. Puede debatirse si esta asunción es válida.
Una famosa observación atribuida a Gabriel Lippmann dice:[cita requerida]
Todo el mundo cree en la ley normal de los errores: los matemáticos, porque piensan que es un hecho experimental; y los experimentadores, porque suponen que es un teorema matemático
Otra fuente podría ser Henri Poincaré.
[editar] Características físicas de especímenes biológicos
Los tamaños de los animales adultos siguen aproximadamente una distribución log-normal. La evidencia y explicación basada en modelos de crecimiento fue publicada por primera vez en el libro Problemas de crecimiento relativo, de 1932, por Julian Huxley.
Las diferencias de tamaño debido a dimorfismos sexuales u otros polimorfismos de insectos, como la división social de las abejas en obreras, zánganos y reinas, por ejemplo, hace que la distribución de tamaños se desvíe hacia la lognormalidad.
La asunción de que el tamaño lineal de los especímenes biológicos es normal (más que lognormal) nos lleva a una distribución no normal del peso (puesto que el peso o el volumen es proporcional al cuadrado o el cubo de la longitud y las distribuciones gaussianas sólo mantienen las transformaciones lineales). A la inversa, asumir que el peso sigue una distribución normal implica longitudes no normales. Esto es un problema porque, a priori, no hay razón por la que cualquiera de ellas (longitud, masa corporal u otras) debería estar normalmente distribuida. Las distribuciones lognormales, por otro lado, se mantienen entre potencias, así que el "problema" se desvanece si se asume la lognormalidad.
Por otra parte, hay algunas medidas biológicas donde se asume normalidad, tales como la presión sanguínea en humanos adultos. Esta asunción sólo es posible tras separar a hombres y mujeres en distintas poblaciones, cada una de las cuales está normalmente distribuida.
[editar] Variables financieras

El modelo normal de movimiento de activos no incluye movimientos extremos tales como
quiebras financieras.
Ya en 1900 Louis Bachelier propuso representar los precios de cambio usando la distribución normal. Esta aproximación se ha modificado desde entonces ligeramente. A causa de la naturaleza multiplicativa del interés compuesto, los indicadores financieros como valores de mercado y precios de las materias primas exhiben un "comportamiento multiplicativo". Como tales, sus cambios periódicos (por ejemplo, cambios anuales) no son normales, sino lognormales. Esta es todavía la hipótesis más comúnmente aceptada en economía.
No obstante, en realidad las variables financieras exhiben colas pesadas y así, la asunción de normalidad infravalora la probabilidad de eventos extremos como quiebras financieras. Se han sugerido correcciones a este modelo por parte de matemáticos como Benoît Mandelbrot, quien observó que los cambios en el logaritmo durante breves periodos de tiempo (como un día) se aproximan bien por distribuciones que no tienen una varianza finita y, por consiguiente, el teorema central del límite no puede aplicarse. Más aún, la suma de muchos de tales cambios sigue una distribución de log-Levy.
[editar] Distribuciones en tests de inteligencia
A veces, la dificultad y número de preguntas en un test de inteligencia se selecciona de modo que proporcionen resultados normalmente distribuidos. Más aún, las puntuaciones "en crudo" se convierten a valores que marcan el cociente intelectual ajustándolas a la distribución normal. En cualquier caso se trata de un resultado causado deliberadamente por la construcción del test o de una interpretación de las puntuaciones que sugiere normalidad para la mayoría de la población. Sin embargo, la cuestión acerca de si la inteligencia en sí está normalmente distribuida es más complicada porque se trata de una variable latente y, por consiguiente, no puede observarse directamente.
[editar] Ecuación de difusión
La función de densidad de la distribución normal está estrechamente relacionada con la ecuación de difusión (homogénea e isótropa) y, por tanto, también con la ecuación de calor. Esta ecuación diferencial parcial describe el tiempo de evolución de una función de densidad bajo difusión. En particular, la función de densidad de masa
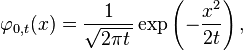
para la distribución normal con esperanza 0 y varianza t satisface la ecuación de difusión:
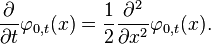
Si la densidad de masa para un tiempo t = 0 viene dada por la delta de Dirac, lo cual significa, esencialemente que toda la masa está inicialmente concentrada en un punto, entonces la función de densidad de masa en el tiempo t tendrá la forma de la función de densidad de la normal, con varianza creciendo linealmente con t. Esta conexión no es coincidencia: la difusión se debe a un movimiento Browniano que queda descrito matemáticamente por un proceso de Wiener, y tal proceso en un tiempo t también resultará normal con varianza creciendo linealmente con t'.
Más generalmente, si la densidad de masa inicial viene dada por una función φ(x), entonces la densidad de masa en un tiempo t vendrá dada por la convolución de φ y una función de densidad normal.
[editar] Uso en estadística computacional
[editar] Generación de valores para una variable aleatoria normal
Para simulaciones por ordenador es útil, en ocasiones, generar valores que podrían seguir una distribución normal. Hay varios métodos y el más básico de ellos es invertir la función de distribución de la normal estándar. Se conocen otros métodos más eficientes, uno de los cuales es la transformacion de Box-Muller. Un algoritmo incluso más rápido es el algoritmo zigurat. Ambos se discuten más abajo. Una aproximación simple a estos métodos es programarlos como sigue: simplemente súmense 12 desviaciones uniformes (0,1) y réstense 6 (la mitad de 12). Esto es bastante útil en muchas aplicaciones. La suma de esos 12 valores sigue la distribución de Irwin-Hall; son elegidos 12 para dar a la suma una varianza de uno, exactamente. Las desviaciones aleatorias resultantes están limitadas al rango (−6, 6) y tienen una densidad que es una doceava sección de una aproximación polinomial de undécimo orden a la distribución normal .[10]
El método de Box-Muller dice que, si tienes dos números aleatorios U y V uniformemente distribuidos en (0, 1], (por ejemplo, la salida de un generador de números aleatorios), entonces X e Y son dos variables aleatorias estándar normalmente distribuidas, donde:
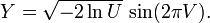
Esta formulación aparece porque la distribución χ² con dos grados de libertad (véase la propiedad 4, más arriba) es una variable aleatoria exponencial fácilmente generada (la cual corresponde a la cantidad lnU en estas ecuaciones). Así, un ángulo elegido uniformemente alrededor de un círculo vía la variable aleatoria V y un radio elegido para ser exponencial se transforman entonces en coordenadas x e y normalmente distribuidas.
Un método mucho más rápido que la transformación de Box-Muller, pero que sigue siendo exacto es el llamado algoritmo Zigurat, desarrollado por George Marsaglia. En alrededor del 97% de los casos usa sólo dos números aleatorios, un entero aleatorio y un uniforme aleatorio, una multiplicación y un test-si . Sólo un 3% de los casos donde la combinación de estos dos cae fuera del "corazón del zigurat", un tipo de rechazo muestral usando logaritmos, exponenciales y números aleatorios más uniformes deberían ser empleados.
Hay también alguna investigación sobre la conexión entre la rápida transformación de Hadamard y la distribución normal, en virtud de que la transformación emplea sólo adición y sustracción y por el teorema central del límite los números aleatorios de casi cualquier distribución serán transformados en la distribución normal. En esta visión se pueden combinar una serie de transformaciones de Hadamard con permutaciones aleatorias para devolver conjuntos de datos aleatorios normalmente distribuidos.
[editar] Aproximaciones numéricas de la distribución normal y su función de distribución
La función de distribución normal se usa extensamente en computación científica y estadística. Por consiguiente, ha sido implementada de varias formas.
La Biblioteca Científica GNU calcula valores de la función de distribución normal estándar usando aproximaciones por funciones racionales a trozos. Otro método de aproximación usa polinomios de tercer grado en intervalos.[11] El artículo sobre el lenguaje de programación bc proporciona un ejemplo de cómo computar la función de distribución en GNU bc.
Para una discusión más detallada sobre cómo calcular la distribución normal, véase la sección 3.4.1C. de The Art of Computer Programming (El arte de la programación por ordenador), de Knuth.
[editar] Véase también
[editar] Referencias
- ↑ Es una consecuencia del Teorema Central del Límite
- ↑ Abraham de Moivre, "Approximatio ad Summam Terminorum Binomii (a + b)n in Seriem expansi" (impreso el 12 de noviembre de 1733 en Londres para una edición privada). Este panfleto se reimprimió en: (1) Richard C. Archibald (1926) “A rare pamphlet of Moivre and some of his discoveries,” Isis, vol. 8, páginas 671-683; (2) Helen M. Walker, “De Moivre on the law of normal probability” en David Eugene Smith, A Source Book in Mathematics [Nueva York, Nueva York: McGraw-Hill, 1929; reimpresión: Nueva York, Nueva York: Dover, 1959], vol. 2, páginas 566-575.; (3) Abraham De Moivre, The Doctrine of Chances (2ª ed.) [Londres: H. Woodfall, 1738; reimpresión: Londres: Cass, 1967], páginas 235-243; (3ª ed.) [Londres: A Millar, 1756; reimpresión: Nueva York, Nueva York: Chelsea, 1967], páginas 243-254; (4) Florence N. David, Games, Gods and Gambling: A History of Probability and Statistical Ideas [Londres: Griffin, 1962], Apéndice 5, páginas 254-267.
- ↑ Havil, 2003
- ↑ Wussing, Hans. «Lección 10». Lecciones de Historia de las Matemáticas (1ª (castellano) edición). Siglo XXI de España Editores, S.A.. pp. 190. ISBN 84-323-0966-4. http://books.google.es/books?id=IG3_b5Xm8PMC. «"La distribución normal y sus aplicaciones a la teoría de errores se asocia a menudo con el nombre de Gauss, quien la descubrió -igual que Laplace- independientemente; no obstante ya había sido estudiada por de Moivre»
- ↑ Weisstein, Eric W., «Normal Distribution» (en inglés), MathWorld, Wolfram Research, http://mathworld.wolfram.com/NormalDistribution.html, consultado el 18 de marzo .
- ↑ La función Q
- ↑ http://www.eng.tau.ac.il/~jo/academic/Q.pdf
- ↑ Weisstein, Eric W., «Normal Distribution Function» (en inglés), MathWorld, Wolfram Research, http://mathworld.wolfram.com/NormalDistributionFunction.html .
- ↑ M.A. Sanders. «Characteristic function of the univariate normal distribution». Consultado el 06-03-2009.
- ↑ Johnson NL, Kotz S, Balakrishnan N. (1995) Continuous Univariate Distributions Volume 2, Wiley. Equation(26.48)
- ↑ Andy Salter. «B-Spline curves». Consultado el 05-12-2008.
[editar] Enlaces externos
Se puede usar software y un programa de computadora para el ajuste de una distribución de probabilidad, incluyendo la normal, a una serie de datos:
- Easy fit, "data analysis & simulation"
- MathWorks Benelux
- ModelRisk, "risk modelling software"
- Ricci distributions, fitting distrubutions with R , Vito Ricci, 2005
- Risksolver, automatically fit distributions and parameters to samples
- StatSoft distribution fitting
- CumFreq [1] , libre sin costo, incluye la distribución normal, la lognormal, raíz-normal, cuadrado-normal, e intervalos de confianza a base de la distribución binomial
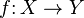 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota 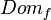 o bien
o bien 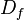 y está definido por:
y está definido por: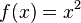 El dominio de esta función es
El dominio de esta función es 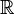
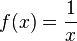 El dominio de esta función es
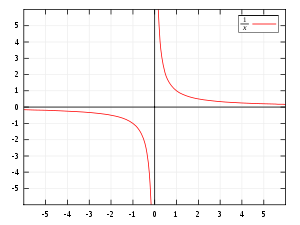
El dominio de esta función es 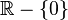 puesto que la función no está definida para x = 0.
puesto que la función no está definida para x = 0.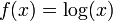 El dominio de esta función es
El dominio de esta función es 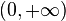 ya que los logaritmos están definidos sólo para números positivos.
ya que los logaritmos están definidos sólo para números positivos.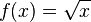 El dominio de esta función es
El dominio de esta función es 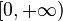 porque la raíz de un número negativo no existe en el campo de los Reales.
porque la raíz de un número negativo no existe en el campo de los Reales.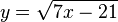
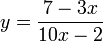 no estará definida cuando 10x − 2 = 0, despejando x = 1 / 5, es decir la variable x debe tener un valor diferente para poder existir, ya que en ese punto no está definida, por tanto el dominio de esta función será el conjunto de todos los reales menos ese punto. Su notación será R-{1/5}, que se lee, el conjunto de todos los reales menos el punto 0,20.
no estará definida cuando 10x − 2 = 0, despejando x = 1 / 5, es decir la variable x debe tener un valor diferente para poder existir, ya que en ese punto no está definida, por tanto el dominio de esta función será el conjunto de todos los reales menos ese punto. Su notación será R-{1/5}, que se lee, el conjunto de todos los reales menos el punto 0,20.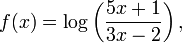
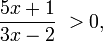
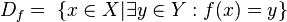
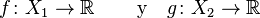
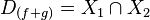
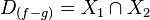
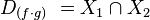
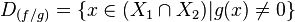
 es el número que,
es el número que,  .
.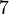 es
es 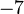 , porque
, porque 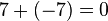 ;
;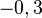 es
es 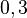 , porque
, porque 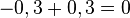 .
.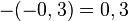 .
.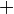 " (cuando se usa la
" (cuando se usa la 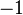 , es decir,
, es decir, 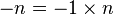
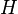 el Hamiltoniano de un sistema físico. De acuerdo con lo antes mencionado, el mismo se puede escribir como
el Hamiltoniano de un sistema físico. De acuerdo con lo antes mencionado, el mismo se puede escribir como 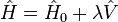 , donde
, donde 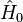 corresponde al Hamiltoniano sin pertubar (cuyas soluciones se conocen) y
corresponde al Hamiltoniano sin pertubar (cuyas soluciones se conocen) y 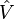 es el potencial que modifica a
es el potencial que modifica a 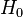 . El parámetro
. El parámetro 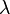 controla la magnitud de la perturbación. En general es un parámetro ficticio que se usa por conveniencia matemática y que al final del análisis se toma
controla la magnitud de la perturbación. En general es un parámetro ficticio que se usa por conveniencia matemática y que al final del análisis se toma 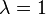 . Por otro lado, los autoestados de
. Por otro lado, los autoestados de 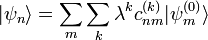
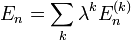
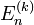 es la
es la 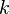 indica el orden de la corrección comenzando por
indica el orden de la corrección comenzando por 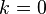 . Es decir, cuanto mayor sea
. Es decir, cuanto mayor sea 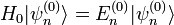 y
y 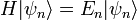
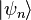 en la segunda ecuación de la anterior línea se tiene
en la segunda ecuación de la anterior línea se tiene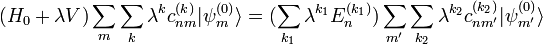
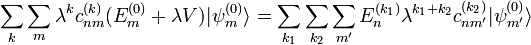
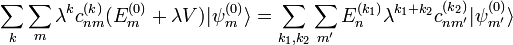
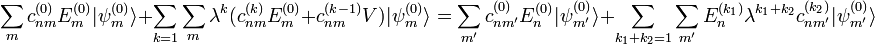
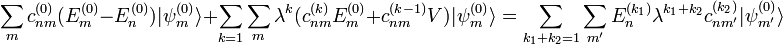
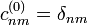 , donde
, donde 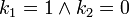 o bien cuando
o bien cuando 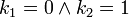 . Por lo tanto se tiene
. Por lo tanto se tiene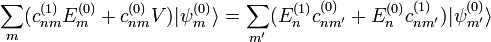
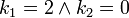 ,
, 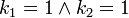 y
y 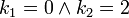 , entonces
, entonces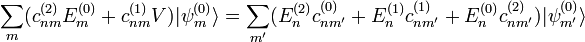
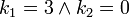 ,
, 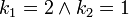 ,
, 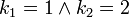 y
y 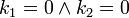 , entonces
, entonces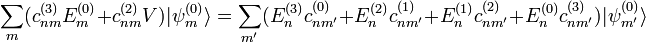
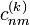 de las combinaciones lineales y las correcciones a las energías
de las combinaciones lineales y las correcciones a las energías 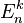 . Para obtenerlas se procede del siguiente modo: primero se usa el hecho que
. Para obtenerlas se procede del siguiente modo: primero se usa el hecho que 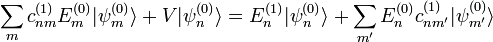
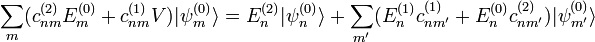
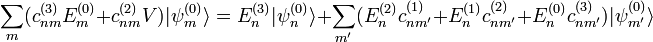
 y usar que
y usar que 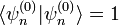 , obteniéndose entonces
, obteniéndose entonces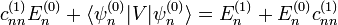
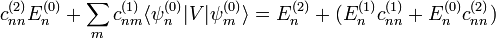
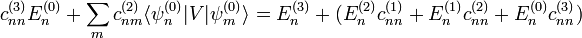
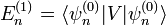
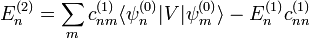
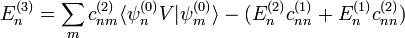
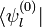 con
con 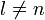 se tiene
se tiene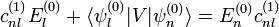
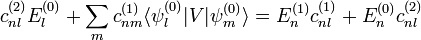
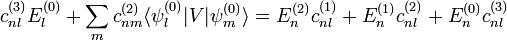
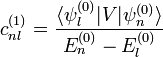
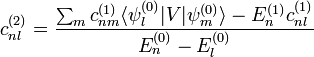
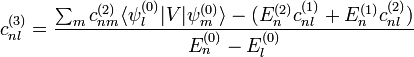
 se calculan por normalización del estado
se calculan por normalización del estado 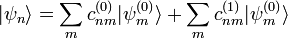 y
y 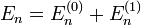
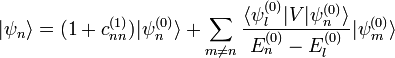 y
y 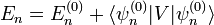
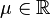
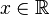
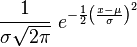
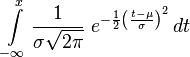
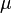
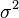
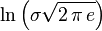
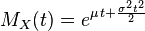
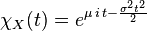

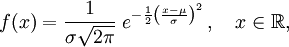
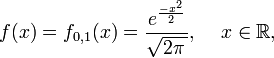
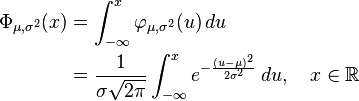
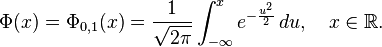
![Phi(x) =frac{1}{2} Bigl[ 1 + operatorname{erf} Bigl( frac{x}{sqrt{2}} Bigr) Bigr], quad xinmathbb{R},](https://petalofucsia.blogia.com/upload/externo-9121802473a43886e7e45fdd9f943fbe.png)
![Phi_{mu,sigma^2}(x) =frac{1}{2} Bigl[ 1 + operatorname{erf} Bigl( frac{x-mu}{sigmasqrt{2}} Bigr) Bigr], quad xinmathbb{R}.](https://petalofucsia.blogia.com/upload/externo-da500c9272562208ae0fbbac30128df9.png)
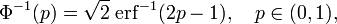
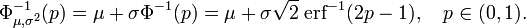
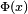 es muy próxima a 1 y
es muy próxima a 1 y 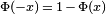 está muy cerca de 0. Los límites elementales
está muy cerca de 0. Los límites elementales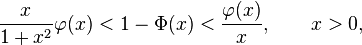
 son útiles.
son útiles.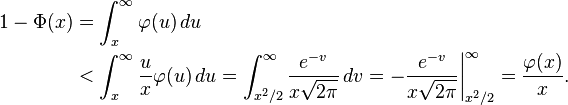
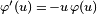 y la
y la 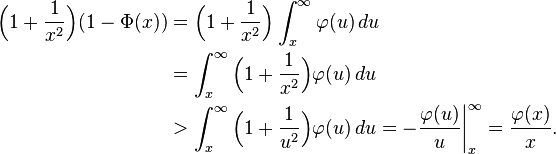
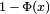 proporciona el límite inferior.
proporciona el límite inferior.![M_X(t) = mathrm{E} left[ e^{tX} right] = int_{-infty}^{infty} frac{1}{sigma sqrt{2pi} } e^{-frac{(x - mu)^2}{2 sigma^2}} e^{tx} , dx = e^{mu t + frac{sigma^2 t^2}{2}}](https://petalofucsia.blogia.com/upload/externo-59ef7a28f5657844fd57dce74a826b25.png)
![begin{align} chi_X(t;mu,sigma) &{} = M_X(i t) = mathrm{E} left[ e^{i t X} right] &{}= int_{-infty}^{infty} frac{1}{sigma sqrt{2pi}} e^{- frac{(x - mu)^2}{2sigma^2}} e^{i t x} , dx &{}= e^{i mu t - frac{sigma^2 t^2}{2}} end{align}](https://petalofucsia.blogia.com/upload/externo-4d61a4ac57cb1529ad0d807e2c3a971e.png)

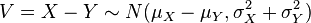 .
.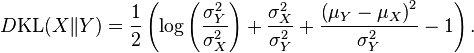
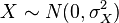 e
e 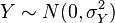 son variables aleatorias independientes normalmente distribuidas, entonces:
son variables aleatorias independientes normalmente distribuidas, entonces: 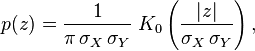 donde
donde 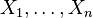 son variables normales estándar independientes, entonces
son variables normales estándar independientes, entonces 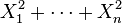 sigue una
sigue una 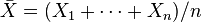 y la
y la 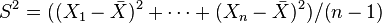 son independientes. Esta propiedad
son independientes. Esta propiedad 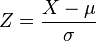
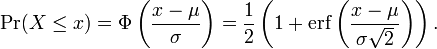
![Eleft[X^{2k}right]=frac{(2k)!}{2^k k!} sigma^{2k}.](https://petalofucsia.blogia.com/upload/externo-ecd1b3e124ecd1cab539b6ac0cb45ed2.png)


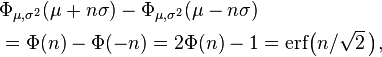
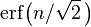
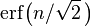
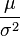 y
y 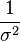 y
y 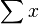 y
y 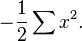
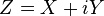
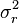 . La función de distribución de la variable conjunta es entonces
. La función de distribución de la variable conjunta es entonces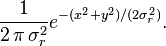
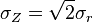 , la función de distribución resultante para la variable gaussiana compleja Z es
, la función de distribución resultante para la variable gaussiana compleja Z es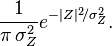
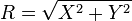 donde
donde 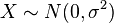 y
y 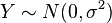 son dos distribuciones normales independientes.
son dos distribuciones normales independientes.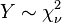 es una
es una 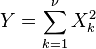 donde
donde 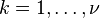 y son independientes.
y son independientes.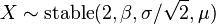 entonces
entonces 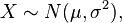 entonces truncando X por debajo de
entonces truncando X por debajo de 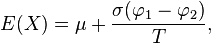 donde
donde 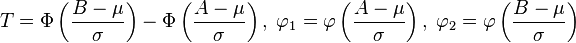 y
y 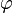 es la función de densidad de una variable normal estándar.
es la función de densidad de una variable normal estándar.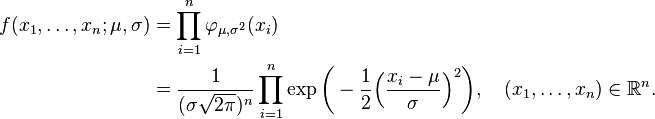
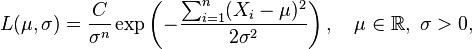
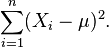
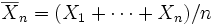
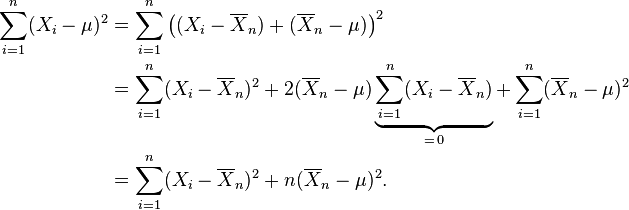
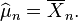
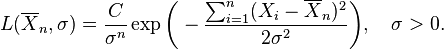
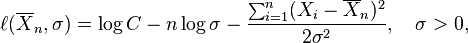
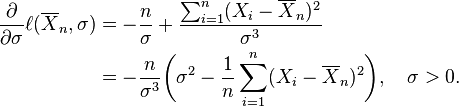
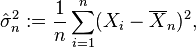
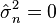 por esta fórmula, refleja el hecho de que en estos casos la función de verosimilitud es ilimitada cuando σ decrece hasta cero.)
por esta fórmula, refleja el hecho de que en estos casos la función de verosimilitud es ilimitada cuando σ decrece hasta cero.)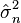 es
es 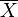 de máxima verosimilitud de la media poblacional μ, es un
de máxima verosimilitud de la media poblacional μ, es un 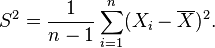
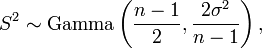
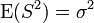 y varianza
y varianza 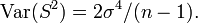

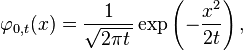
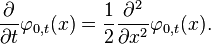
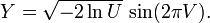

![I[f]=int_a^b f(x,p(r),c'(x),...),dx](https://petalofucsia.blogia.com/upload/externo-51d1dc1a7e160c28d97a8c7e5ef6978e.png)
![I[f]=int_a^b f(x) dx =](https://petalofucsia.blogia.com/upload/externo-0fb1342788f1ec5da585c597b09d59e9.png) max
max![G[f] = int_a^b sqrt{1+(f'(x))^2} dx = l](https://petalofucsia.blogia.com/upload/externo-8594a87a47b2fba514b056f4c5e92723.png) (longitud de arco)
(longitud de arco)![T[f]=int_{0}^{x_0}frac {sqrt{1+(f'(x))^2}} {sqrt{2g(y_0-y)}} dx =](https://petalofucsia.blogia.com/upload/externo-c8c350f6b98d836486d56fc24b19a533.png) min
min