De Wikipedia, la enciclopedia libre
En matemáticas, ciencias de la computación y disciplinas relacionadas, un algoritmo (del griego y latin, dixit algorithmus y éste a su vez del matemático persa Al Juarismi[1] ) es un conjunto preescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permite realizar una actividad mediante pasos sucesivos que no generen dudas a quien deba realizar dicha actividad.[2] Dados un estado inicial y una entrada, siguiendo los pasos sucesivos se llega a un estado final y se obtiene una solución. Los algoritmos son el objeto de estudio de la algoritmia.[1]
En la vida cotidiana, se emplean algoritmos frecuentemente para resolver problemas. Algunos ejemplos son los manuales de usuario, que muestran algoritmos para usar un aparato, o las instrucciones que recibe un trabajador por parte de su patrón. Algunos ejemplos en matemática son el algoritmo de la división para calcular el cociente de dos números, el algoritmo de Euclides para obtener el máximo común divisor de dos enteros positivos, o el método de Gauss para resolver un sistema lineal de ecuaciones.
PROBLEMA -> ALGORITMO -> PROGRAMA
El pseudocódigo es una herramienta algorítmica que permite escribir pseudoprogramas (una imitación de un programa real) utilizando un lenguaje de pseudoprogramación que es una imitación de los lenguajes de programación de alto nivel. Así, un pseudocódigo es una combinación de símbolos (+, -, *, /, %, >, >=, <, <=, !=, ==, y, o, no), términos (Leer, Imprimir, Abrir, Cerrar, Hacer...Mientras, Mientras...Hacer, Para...Mientras, etc) y otras características comúnmente utilizadas en uno o más lenguajes de alto nivel.
No existen reglas que determinen que es o no es un pseudocódigo, sino que varía de un programador a otro. El objetivo del pseudocódigo es permitir al programador centrarse en los aspectos lógicos de la solución evitando las reglas de sintáxis de un lenguaje de programación. Posteriormente el pseudocódigo debe ser traducido a programa usando un lenguaje de programación de alto nivel como Java, C++, C, etc.
Ejemplo 2.1:- Diseñe un algoritmo para preparar una limonada.
INICIO Llenar una jarra con un litro de agua Echar el jugo de tres limones Echar cuatro cucharadas de azúcar Remover el agua hasta disolver completamente el azúcar FIN
Ejemplo 2.2 :- Diseñe un algoritmo que permita hallar la suma y el promedio de tres números.
INICIO LEER numero1, numero2, numero3 suma = numero1 + numero2 + numero3 promedio = suma / 3 IMPRIMIR suma, promedio FIN
Notas:-
- El témino LEER significa obtener un dato de algún dispositivo de entrada, como el teclado, y almacenarlo en una variable.
Una variable es una localización en la memoria que tiene un nombre y cuyo contenido puede cambiar a lo largo de la ejecución de un programa. Así numero1, numero2 y numero3 son variables.
- El término IMPRIMIR significa mostrar el valor de una variable en algún dispositivo de salida, como la pantalla.
[editar] Características principales y definición formal
En general, no existe ningún consenso definitivo en cuanto a la definición formal de algoritmo. Muchos autores los señalan como listas de instrucciones para resolver un problema abstracto, es decir, que un número finito de pasos convierten los datos de un problema (entrada) en una solución (salida).[1] [2] [3] [4] [5] [6] Sin embargo cabe notar que algunos algoritmos no necesariamente tienen que terminar o resolver un problema en particular. Por ejemplo, una versión modificada de la criba de Eratóstenes que nunca termine de calcular números primos no deja de ser un algoritmo.[7]
A lo largo de la historia varios autores han tratado de definir formalmente a los algoritmos utilizando modelos matemáticos como máquinas de Turing entre otros.[8] [9] Sin embargo, estos modelos están sujetos a un tipo particular de datos como son números, símbolos o gráficas mientras que, en general, los algoritmos funcionan sobre una vasta cantidad de estructuras de datos.[3] [1] En general, la parte común en todas las definiciones se puede resumir en las siguientes tres propiedades siempre y cuando no consideremos algoritmos paralelos:[7]
Tiempo secuencial. Un algoritmo funciona en tiempo discretizado –paso a paso–, definiendo así una secuencia de estados "
computacionales" por cada entrada válida (la
entrada son los datos que se le suministran al algoritmo antes de comenzar).
Estado abstracto. Cada estado computacional puede ser descrito formalmente utilizando una
estructura de primer orden y cada algoritmo es independiente de su implementación (los algoritmos son objetos abstractos) de manera que en un algoritmo las estructuras de primer orden son invariantes bajo isomorfismo.
Exploración acotada. La transición de un estado al siguiente queda completamente determinada por una descripción fija y finita; es decir, entre cada estado y el siguiente solamente se puede tomar en cuenta una cantidad fija y limitada de términos del estado actual.
En resumen, un algoritmo es cualquier cosa que funcione paso a paso, donde cada paso se pueda describir sin ambigüedad y sin hacer referencia a una computadora en particular, y además tiene un límite fijo en cuanto a la cantidad de datos que se pueden leer/escribir en un solo paso. Esta amplia definición abarca tanto a algoritmos prácticos como aquellos que solo funcionan en teoría, por ejemplo el método de Newton y la eliminación de Gauss-Jordan funcionan, al menos en principio, con números de precisión infinita; sin embargo no es posible programar la precisión infinita en una computadora, y no por ello dejan de ser algoritmos.[10] En particular es posible considerar una cuarta propiedad que puede ser usada para validar la tesis de Church-Turing de que toda función calculable se puede programar en una máquina de Turing (o equivalentemente, en un lenguaje de programación suficientemente general):[10]
Aritmetizabilidad. Solamente operaciones innegablemente calculables están disponibles en el paso inicial.
[editar] Medios de expresión de un algoritmo
Los algoritmos pueden ser expresados de muchas maneras, incluyendo al lenguaje natural, pseudocódigo, diagramas de flujo y lenguajes de programación entre otros. Las descripciones en lenguaje natural tienden a ser ambiguas y extensas. El usar pseudocódigo y diagramas de flujo evita muchas ambigüedades del lenguaje natural. Dichas expresiones son formas más estructuradas para representar algoritmos; no obstante, se mantienen independientes de un lenguaje de programación específico.
La descripción de un algoritmo usualmente se hace en tres niveles:
- Descripción de alto nivel. Se establece el problema, se selecciona un modelo matemático y se explica el algoritmo de manera verbal, posiblemente con ilustraciones y omitiendo detalles.
- Descripción formal. Se usa pseudocódigo para describir la secuencia de pasos que encuentran la solución.
- Implementación. Se muestra el algoritmo expresado en un lenguaje de programación específico o algún objeto capaz de llevar a cabo instrucciones.
También es posible incluir un teorema que demuestre que el algoritmo es correcto, un análisis de complejidad o ambos.
[editar] Diagrama de flujo
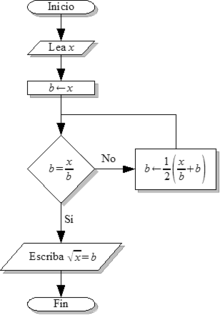
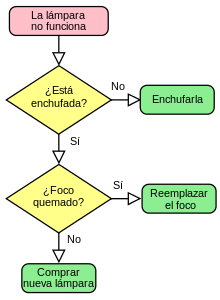
Diagrama de flujo que expresa un algoritmo para calcular la raíz cuadrada de un número
x Los diagramas de flujo son descripciones gráficas de algoritmos; usan símbolos conectados con flechas para indicar la secuencia de instrucciones y están regidos por ISO.
Los diagramas de flujo son usados para representar algoritmos pequeños, ya que abarcan mucho espacio y su construcción es laboriosa. Por su facilidad de lectura son usados como introducción a los algoritmos, descripción de un lenguaje y descripción de procesos a personas ajenas a la computación.
[editar] Pseudocódigo
El pseudocódigo (falso lenguaje, el prefijo pseudo significa falso) es una descripción de alto nivel de un algoritmo que emplea una mezcla de lenguaje natural con algunas convenciones sintácticas propias de lenguajes de programación, como asignaciones, ciclos y condicionales, aunque no está regido por ningún estándar. Es utilizado para describir algoritmos en libros y publicaciones científicas, y como producto intermedio durante el desarrollo de un algoritmo, como los |diagramas de flujo, aunque presentan una ventaja importante sobre estos, y es que los algoritmos descritos en pseudocódigo requieren menos espacio para representar instrucciones complejas.
El pseudocódigo está pensado para facilitar a las personas el entendimiento de un algoritmo, y por lo tanto puede omitir detalles irrelevantes que son necesarios en una implementación. Programadores diferentes suelen utilizar convenciones distintas, que pueden estar basadas en la sintaxis de lenguajes de programación concretos. Sin embargo, el pseudocódigo en general es comprensible sin necesidad de conocer o utilizar un entorno de programación específico, y es a la vez suficientemente estructurado para que su implementación se pueda hacer directamente a partir de él.
[editar] Sistemas formales
La teoría de autómatas y la teoría de funciones recursivas proveen modelos matemáticos que formalizan el concepto de algoritmo. Los modelos más comunes son la máquina de Turing, máquina de registro y funciones μ-recursivas. Estos modelos son tan precisos como un lenguaje máquina, careciendo de expresiones coloquiales o ambigüedad, sin embargo se mantienen independientes de cualquier computadora y de cualquier implementación.
[editar] Implementación
Muchos algoritmos son ideados para implementarse en un programa. Sin embargo, los algoritmos pueden ser implementados en otros medios, como una red neuronal, un circuito eléctrico o un aparato mecánico y eléctrico. Algunos algoritmos inclusive se diseñan especialmente para implementarse usando lápiz y papel. El algoritmo de multiplicación tradicional, el algoritmo de Euclides, la criba de Eratóstenes y muchas formas de resolver la raíz cuadrada son sólo algunos ejemplos.
Un elemento que toda pertenece a un dato específico correcto. La declaración se realiza comenzando con var. Principalmente, existen dos maneras de otorgar valores iniciales a variables:
- Mediante una sentencia de asignación.
- Mediante uno de los procedimientos de entrada de datos (read o readln).
Ejemplo:
...
i:=1;
readln(n);
while i < n do begin
(* cuerpo del bucle *)
i := i + 1
end;
...
[editar] Estructuras secuenciales
La estructura secuencial es aquella en la que una acción sigue a otra en secuencia. Las operaciones se suceden de tal modo que la salida de una es la entrada de la siguiente y así sucesivamente hasta el fin del proceso. La asignación de esto consiste, en el paso de valores o resultados a una zona de la memoria. Dicha zona será reconocida con el nombre de la variable que recibe el valor. La asignación se puede clasificar de la siguiente forma:
- Simples: Consiste en pasar un valor constante a una variable (a <= 15)
- Contador: Consiste en usarla como un verificador del numero de veces que se realiza un proceso (a <= a + 1)
- Acumulador: Consiste en usarla como un sumador en un proceso (a <= a + b)
- De trabajo: Donde puede recibir el resultado de una operación matemática que involucre muchas variables (a <= c + b*2/4).
Un ejemplo de estructura secuencial, como obtener la área de un triángulo:
Inicio
...
int b, h, a;
printf("Diga la base", b);
scanf(%i, b);
printf("Diga la altura", h);
scanf(%i, h)
a := (b*h)/2
printf("El área del triángulo es de", a)
...
Fin
[editar] Algoritmos como funciones
Un algoritmo se puede concebir como una función que transforma los datos de un problema (entrada) en los datos de una solución (salida). Más aún, los datos se pueden representar a su vez como secuencias de bits, y en general, de símbolos cualesquiera.[1] [9] [11] Como cada secuencia de bits representa a un número natural (véase Sistema binario), entonces los algoritmos son en esencia funciones de los números naturales en los números naturales que sí se pueden calcular. Es decir que todo algoritmo calcula una función 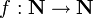 donde cada número natural es la codificación de un problema o de una solución.
donde cada número natural es la codificación de un problema o de una solución.
En ocasiones los algoritmos son susceptibles de nunca terminar, por ejemplo, cuando entran a un bucle infinito. Cuando esto ocurre, el algoritmo nunca devuelve ningún valor de salida, y podemos decir que la función queda indefinida para ese valor de entrada. Por esta razón se considera que los algoritmos son funciones parciales, es decir, no necesariamente definidas en todo su dominio de definición.
Cuando una función puede ser calculada por medios algorítmicos, sin importar la cantidad de memoria que ocupe o el tiempo que se tarde, se dice que dicha función es computable. No todas las funciones entre secuencias datos son computables. El problema de la parada es un ejemplo.
[editar] Análisis de algoritmos
Como medida de la eficiencia de un algoritmo, se suelen estudiar los recursos (memoria y tiempo) que consume el algoritmo. El análisis de algoritmos se ha desarrollado para obtener valores que de alguna forma indiquen (o especifiquen) la evolución del gasto de tiempo y memoria en función del tamaño de los valores de entrada.
El análisis y estudio de los algoritmos es una disciplina de las ciencias de la computación y, en la mayoría de los casos, su estudio es completamente abstracto sin usar ningún tipo de lenguaje de programación ni cualquier otra implementación; por eso, en ese sentido, comparte las características de las disciplinas matemáticas. Así, el análisis de los algoritmos se centra en los principios básicos del algoritmo, no en los de la implementación particular. Una forma de plasmar (o algunas veces "codificar") un algoritmo es escribirlo en pseudocódigo o utilizar un lenguaje muy simple tal como Lexico, cuyos códigos pueden estar en el idioma del programador.
Algunos escritores restringen la definición de algoritmo a procedimientos que deben acabar en algún momento, mientras que otros consideran procedimientos que podrían ejecutarse eternamente sin pararse, suponiendo el caso en el que existiera algún dispositivo físico que fuera capaz de funcionar eternamente. En este último caso, la finalización con éxito del algoritmo no se podría definir como la terminación de éste con una salida satisfactoria, sino que el éxito estaría definido en función de las secuencias de salidas dadas durante un periodo de vida de la ejecución del algoritmo. Por ejemplo, un algoritmo que verifica que hay más ceros que unos en una secuencia binaria infinita debe ejecutarse siempre para que pueda devolver un valor útil. Si se implementa correctamente, el valor devuelto por el algoritmo será válido, hasta que evalúe el siguiente dígito binario. De esta forma, mientras evalúa la siguiente secuencia podrán leerse dos tipos de señales: una señal positiva (en el caso de que el número de ceros sea mayor que el de unos) y una negativa en caso contrario. Finalmente, la salida de este algoritmo se define como la devolución de valores exclusivamente positivos si hay más ceros que unos en la secuencia y, en cualquier otro caso, devolverá una mezcla de señales positivas y negativas.
[editar] Ejemplo de algoritmo
El problema consiste en encontrar el máximo de un conjunto de números. Para un ejemplo más complejo véase Algoritmo de Euclides.
[editar] Descripción de alto nivel
Dado un conjunto finito C de números, se tiene el problema de encontrar el número más grande. Sin pérdida de generalidad se puede asumir que dicho conjunto no es vacío y que sus elementos están numerados como 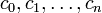 .
.
Es decir, dado un conjunto 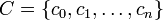 se pide encontrar m tal que
se pide encontrar m tal que 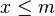 para todo elemento x que pertenece al conjunto C.
para todo elemento x que pertenece al conjunto C.
Para encontrar el elemento máximo, se asume que el primer elemento (c0) es el máximo; luego, se recorre el conjunto y se compara cada valor con el valor del máximo número encontrado hasta ese momento. En el caso que un elemento sea mayor que el máximo, se asigna su valor al máximo. Cuando se termina de recorrer la lista, el máximo número que se ha encontrado es el máximo de todo el conjunto.
[editar] Descripción formal
El algoritmo puede ser escrito de una manera más formal en el siguiente pseudocódigo:
| Algoritmo Encontrar el máximo de un conjunto |
función max(C) //C es un conjunto no vacío de números//n ← | C | // | C | es el número de elementos de C//m ← c0para i ← 1 hasta n hacer si ci > m entonces m ← cidevolver m |
Sobre la notación:
- "←" representa una asignación: m ← x significa que la variable m toma el valor de x;
- "devolver" termina el algoritmo y devuelve el valor a su derecha (en este caso, el máximo de C).
[editar] Implementación
En lenguaje C++:
int max(int c[], int n){
int i, m = c[0];
for (i = 1; i < n; i++)
if (c[i] > m) m = c[i];
return m;
}
[editar] Referencias
- ↑ a b c d e Brassard, Gilles; Bratley, Paul (1997). Fundamentos de Algoritmia. Madrid: PRENTICE HALL. ISBN 84-89660-00-X.
- ↑ a b Real Academia Española. Diccionario de la lengua española "Conjunto ordenado y finito de operaciones que permite hallar la solución de un problema."
- ↑ a b Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford (2009). Introduction to algorithms. Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-53305-8.
- ↑ Ralph P. Grimaldi (1998). «Propiedades de los números enteros: Inducción matemática». Matemáticas Discreta y Combinatoria. México: Addison Wesley Longman de México. ISBN 968-444-324-2.
- ↑ Johnsonbaugh, Richard (2005). «Introducción a la teoría de números». Matemáticas Discretas. México: PEARSON EDUCACIÓN. ISBN 970-26-0637-3.
- ↑ Carl Reynolds & Paul Tymann (2008). Schaum's Outline of Principles of Computer Science. McGraw-Hill. ISBN 978-0-07-146051-4.
- ↑ a b Gurevich, Yuri (2000). «Sequential Abstract State Machines capture Sequential Algorithms». ACM Transactions on Computational Logic 1 (1). ISSN 1529-3785, 77-111. http://research.microsoft.com/en-us/um/people/gurevich/Opera/141.pdf.
- ↑ John E. Savage (1987). The Complexity of Computing. Krieger Publishing Co.. ISBN 089874833X.
- ↑ a b [|Sipser, Michael] (2005). Introduction to the Theory of Computation (2 edición). Course Technology. ISBN 978-0534950972.
- ↑ a b Nachum Dershowitz & Yuri Gurevich (2008). «A natural axiomatization of computability and proof of Church's Thesis». Bulletin of Symbolic Logic 14 (3). ISSN 10798986, 299-350. http://research.microsoft.com/en-us/um/people/gurevich/Opera/188.pdf.
- ↑ [|Kelley, Dean] (1995). Teoría de Autómatas y Lenguajes Formales. Prentice Hall. ISBN 0-13-497777-7.
[editar] Bibliografía
- Fundamentos de Algoritmia, G. Brassard y P. Bratley. (ISBN 848966000)
- The Art of Computer Programming, Knuth, D. E. [quien fue también, el creador del TeX]
- Introduction to Algorithms (2nd ed), Cormen, T. H., Leiserson, C. E., Rivest, R. L. y Stein, C.
- Introduction to Algorithms. A Creative Approach, Mamber, U.
- Algorithms in C (3r ed), Sedgewick, R. (también existen versiones en C++ y Java)
- The Design and Analysis of Computer Algorithms, Aho, A.
[editar] Véase también
[editar] Tipos de algoritmos según su función
[editar] Técnicas de diseño de algoritmos
- Algoritmos voraces (greedy): seleccionan los elementos más prometedores del conjunto de candidatos hasta encontrar una solución. En la mayoría de los casos la solución no es óptima.
- Algoritmos paralelos: permiten la división de un problema en subproblemas de forma que se puedan ejecutar de forma simultánea en varios procesadores.
- Algoritmos probabilísticos: algunos de los pasos de este tipo de algoritmos están en función de valores pseudoaleatorios.
- Algoritmos determinísticos: el comportamiento del algoritmo es lineal: cada paso del algoritmo tiene únicamente un paso sucesor y otro antecesor.
- Algoritmos no determinísticos: el comportamiento del algoritmo tiene forma de árbol y a cada paso del algoritmo puede bifurcarse a cualquier número de pasos inmediatamente posteriores, además todas las ramas se ejecutan simultáneamente.
- Divide y vencerás: dividen el problema en subconjuntos disjuntos obteniendo una solución de cada uno de ellos para después unirlas, logrando así la solución al problema completo.
- Metaheurísticas: encuentran soluciones aproximadas (no óptimas) a problemas basándose en un conocimiento anterior (a veces llamado experiencia) de los mismos.
- Programación dinámica: intenta resolver problemas disminuyendo su coste computacional aumentando el coste espacial.
- Ramificación y acotación: se basa en la construcción de las soluciones al problema mediante un árbol implícito que se recorre de forma controlada encontrando las mejores soluciones.
- Vuelta atrás (backtracking): se construye el espacio de soluciones del problema en un árbol que se examina completamente, almacenando las soluciones menos costosas.
[editar] Temas relacionados
[editar] Disciplinas relacionadas
[editar] Enlaces externos
Wikilibros

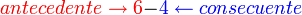
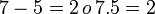
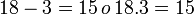

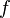 es continua en
es continua en 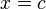 si y sólo si:
si y sólo si: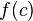 está definido.
está definido.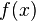 cuando
cuando 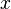 tiende a
tiende a  .
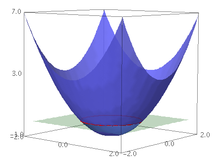
.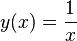 . Esta función posee una singularidad en el punto
. Esta función posee una singularidad en el punto 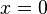 , en dicho punto la función presenta un comportamiento que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función
, en dicho punto la función presenta un comportamiento que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función 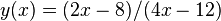 presentará una singularidad en el punto
presentará una singularidad en el punto 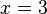 . Otras funciones que contienen singularidades son
. Otras funciones que contienen singularidades son 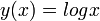 ó
ó 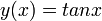 .
.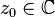 , y una función
, y una función 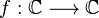 se dice que
se dice que 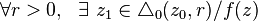 es singular en
es singular en 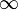 al acercarse a
al acercarse a 

 , si es que dichos supremos existen
, si es que dichos supremos existen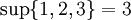
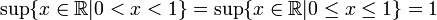
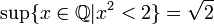



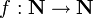 donde cada número natural es la
donde cada número natural es la 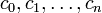 .
.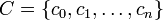 se pide encontrar
se pide encontrar 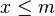 para todo elemento
para todo elemento 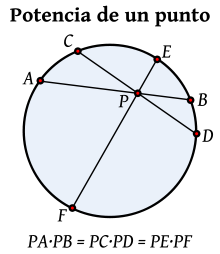
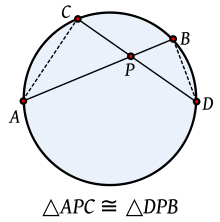
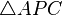 y
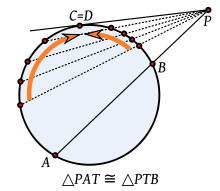
y 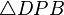 los cuales serán semejantes, pues :
los cuales serán semejantes, pues :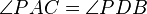 , siendo ambos iguales a la mitad del arco BC.
, siendo ambos iguales a la mitad del arco BC.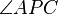 y
y 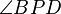 son iguales por ser opuestos por el vértice.
son iguales por ser opuestos por el vértice.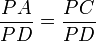
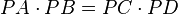 .
.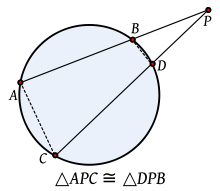
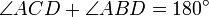 . Por otro lado
. Por otro lado 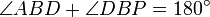 y por tanto
y por tanto 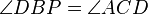 .
.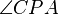 son el mismo ángulo y por tanto iguales entre sí.
son el mismo ángulo y por tanto iguales entre sí.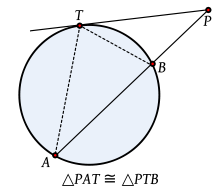
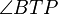 es
es 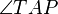 .
.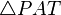 y
y 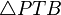 . Dicha semejanza implica
. Dicha semejanza implica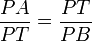
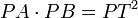 .
.
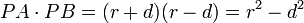 .
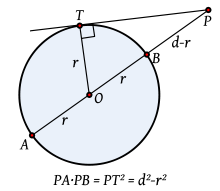
.
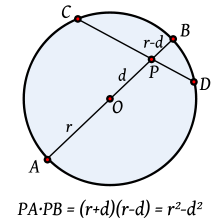
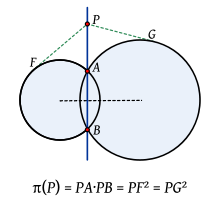
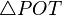 es rectángulo pues una recta tangente es perpendicular a la recta que une el punto de tangencia con el centro del círculo, es decir:
es rectángulo pues una recta tangente es perpendicular a la recta que une el punto de tangencia con el centro del círculo, es decir: 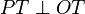 .
.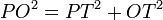
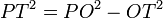
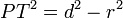 .
.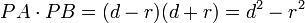 .
.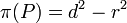
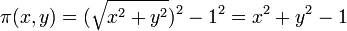 .
.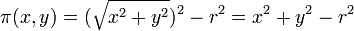 .
.
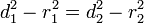 donde
donde 
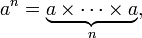
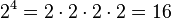 .
.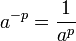
![a^{frac{n}{m}} = sqrt[m]{a^n}](https://petalofucsia.blogia.com/upload/externo-69a226541f1a5be3ae9e0bbc4bbb1c44.png)
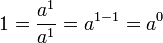
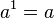
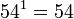
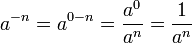
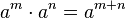
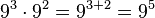
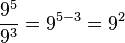
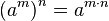
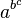 se reserva para significar
se reserva para significar 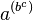 ya que
ya que 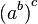 se puede escribir sencillamente como
se puede escribir sencillamente como 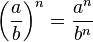
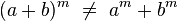
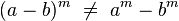
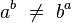
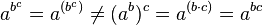
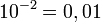
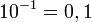
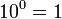
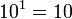
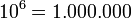
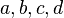 se tiene la identidad:
se tiene la identidad: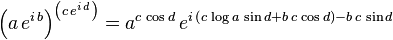
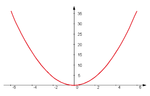
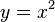
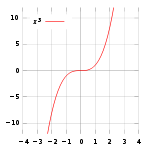
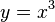
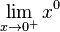
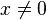 , dicho valor podría ser igual a 1. Sin embargo también puede considerarse dicha expresión como el valor del límite
, dicho valor podría ser igual a 1. Sin embargo también puede considerarse dicha expresión como el valor del límite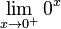
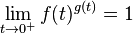 siempre que
siempre que 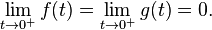
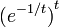
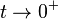 es
es