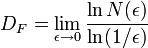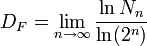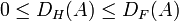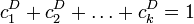De Wikipedia, la enciclopedia libre

En la naturaleza también aparece la geometría fractal, como en esta
romanescu.
Un fractal es un objeto semigeométrico cuya estructura básica, fragmentada o irregular, se repite a diferentes escalas.[1] El término fue propuesto por el matemático Benoît Mandelbrot en 1975 y deriva del Latín fractus, que significa quebrado o fracturado. Muchas estructuras naturales son de tipo fractal.
A un objeto geométrico fractal se le atribuyen las siguientes características:[2]
No basta con una sola de estas características para definir un fractal. Por ejemplo, la recta real no se considera un fractal, pues a pesar de ser un objeto autosimilar carece del resto de características exigidas.
Un fractal natural es un elemento de la naturaleza que puede ser descrito mediante la geometría fractal. Las nubes, las montañas, el sistema circulatorio, las líneas costeras[3] o los copos de nieve son fractales naturales. Esta representación es aproximada, pues las propiedades atribuidas a los objetos fractales ideales, como el detalle infinito, tienen límites en el mundo natural.
[editar] Introducción
La definición de fractal en los años 1970, dio unidad a una serie de ejemplos, algunos de los cuales se remontaban a un siglo atrás:
[editar] Los ejemplos clásicos
Para encontrar los primeros ejemplos de fractales debemos remontarnos a finales del siglo XIX: en 1872 apareció la función de Weierstrass, cuyo grafo hoy en día consideraríamos fractal, como ejemplo de función continua pero no diferenciable en ningún punto.

sucesivos pasos de la construcción de la curva de Koch
Posteriormente aparecieron ejemplos con propiedades similares pero una definición más geométrica. Dichos ejemplos podían construirse partiendo de una figura inicial (semilla), a la que se aplicaban una serie de construcciones geométricas sencillas. La serie de figuras obtenidas se aproximaba a una figura límite que correspondía al que hoy llamamos conjunto fractal. Así, en 1904, Helge von Koch definió una curva con propiedades similares a la de Weierstrass: el copo de nieve de Koch. En 1915, Waclaw Sierpinski construyó su triángulo y, un año después, su alfombra.
Estos conjuntos mostraban las limitaciones del análisis clásico, pero eran vistos como objetos artificiales, una "galería de monstruos", como los denominó Poincaré. Pocos matemáticos vieron la necesidad de estudiar estos objetos en sí mismos.[4]
En 1919 surge una herramienta básica en la descripción y medida de estos conjuntos: la dimensión de Hausdorff-Besicovitch.
[editar] Los conjuntos de Julia
Estos conjuntos, fruto de los trabajos de Pierre Fatou y Gaston Julia en los años 1920, surgen como resultado de la aplicación reiterada de funciones holomorfas 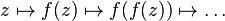 .
.
Analicemos el caso particular de funciones polinómicas de grado mayor que uno. Al aplicar sucesivas veces una función polinómica es muy posible que el resultado tienda a 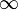 . Al conjunto de valores de
. Al conjunto de valores de 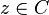 que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.
que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente conjunto de Julia.
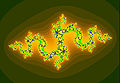
Estos conjuntos se representan mediante un algoritmo de tiempo de escape, en que cada pixel se colorea según el número de iteraciones necesarias para escapar. Suele usarse un color especial, a menudo el negro, para representar los puntos que no han escapado tras un número grande y prefijado de iteraciones.
Ejemplos de conjuntos de Julia para fc(z) = z2 + c En negro, conjunto de Julia relleno asociado a fc, c=φ-2, donde φ es el número áureo | Conjunto de Julia relleno asociado a fc, c=(φ−2)+(φ−1)i =-0.4+0.6i | Conjunto de Julia relleno asociado a fc, c=-0.835-0.2321i |

En negro, imagen del conjunto de Mandelbrot superpuesto con los conjuntos de Julia rellenos representados por algunos de sus puntos (en rojo los conjuntos de Julia conexos y en azul los no conexos).
[editar] Familias de fractales: el conjunto de Mandelbrot
La familia de conjuntos de Julia {fc}, asociadas a la reiteración de funciones de la forma fc(z) = z2 + c presenta conjuntos de una variedad sorprendente.
Dicha familia tendrá especial relevancia al quedar parametrizada en un mapa de fractales, popularizado en los años 1980. llamado conjunto de Mandelbrot. Este conjunto M representa un mapa en que cada pixel, correspondiente a un valor del parámetro 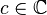 , se colorea de modo que refleje una propiedad básica del conjunto de Julia asociado a fc. En concreto,
, se colorea de modo que refleje una propiedad básica del conjunto de Julia asociado a fc. En concreto, 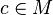 si el conjunto de Julia asociado a fc es conexo.
si el conjunto de Julia asociado a fc es conexo.
[editar] Características de un fractal
[editar] Autosimilitud
Según B. Mandelbrot, un objeto es autosimilar o autosemejante si sus partes tienen la misma forma o estructura que el todo, aunque pueden presentarse a diferente escala y pueden estar ligeramente deformadas.[5]
Los fractales pueden presentar tres tipos de autosimilitud:
- Autosimilitud exacta. este es el tipo más restrictivo de autosimilitud: exige que el fractal parezca idéntico a diferentes escalas. A menudo la encontramos en fractales definidos por sistemas de funciones iteradas (IFS).

Cuasiautosimilitud en el
conjunto de Mandelbrot: al variar la escala obtenemos copias del conjunto con pequeñas diferencias.
- Cuasiautosimilitud: exige que el fractal parezca aproximadamente idéntico a diferentes escalas. Los fractales de este tipo contienen copias menores y distorsionadas de sí mismos. Matemáticamente D.Sullivan definió el concepto de conjunto cuasiauto-similar a partir del concepto de cuasi-isometría. Los fractales definidos por relaciones de recurrencia son normalmente de este tipo.
- Autosimilitud estadística. Es el tipo más débil de autosimilitud: se exige que el fractal tenga medidas numéricas o estadísticas que se preserven con el cambio de escala. Los fractales aleatorios son ejemplos de fractales de este tipo.
[editar] Dimensión fractal y dimensión de Hausdorff-Besicovitch
Entre los fractales podemos encontrar ejemplos como curvas que llenan todo el plano. En ese caso, la dimensión topológica de la curva, que es uno, no nos informa sobre la forma en que esta ocupa el espacio ambiente. De modo general, podríamos preguntarnos cómo densamente un conjunto ocupa el espacio métrico que lo contiene. Los números que nos informan objetivamente de este tipo de cuestiones son:
- La dimensión fractal. Las fórmulas que la definen tienen que ver con el recuento de las bolas necesarias para recubrir el conjunto o con el de cajas de una cuadrícula que contienen parte del conjunto, cuando las dimensiones de unas y otras tienden a cero. Podemos medir la dimensión fractal de objetos reales: líneas de la costa (1.2), nubes, árboles, etc, Con estas medidas podemos comparar objetos del mundo real con fractales generados por algoritmos matemáticos.
- La dimensión de Hausdorff-Besicovitch. Tiene una definición más compleja que la de dimensión fractal. Su definición no suele usarse para comparar conjuntos del mundo real.
[editar] Definición por algoritmos recursivos
Podemos destacar tres técnicas comunes para generar fractales:
- Sistemas de funciones iteradas (IFS). Unos conjuntos se reemplazan recursivamente por su imagen bajo un sistema de aplicaciones: el conjunto de Cantor, la alfombra de Sierpinski, el triángulo de Sierpinski, la curva de Peano, la curva del dragón, el copo de nieve de Koch o la Esponja de Menger, son algunos ejemplos.
- Fractales de algoritmos de Escape, definidos por una relación de recurrencia en cada punto del espacio (por ejemplo, el plano complejo): el conjunto de Mandelbrot, conjunto de Julia, y el fractal de Lyapunov.
- Fractales aleatorios, generados por procesos estocásticos, no deterministas: el movimiento browniano,el vuelo de Lévy, los paisajes fractales o los árboles brownianos. Éstos últimos son producidos por procesos de agregación por difusión limitada..
[editar] Aspectos matemáticos
[editar] Intentos de definición rigurosa
El concepto de fractal no dispone en el año 2008 de una definición matemática precisa y de aceptación general. Intentos parciales de dar una definición fueron realizados por:
- B. Mandelbrot, que en 1982 definió fractal como un conjunto cuya dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica. Él mismo reconoció que su definición no era lo suficientemente general.
- D. Sullivan, que definió matemáticamente una de las categorías de fractales con su definición de conjunto cuasiautosimilar que hacía uso del concepto de cuasi-isometría.
[editar] Dimensión fractal
Puede definirse en términos del mínimo número N(ε) de bolas de radio ε necesarias para recubrir el conjunto, como el límite:
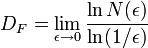
O en función del recuento del número de cajas Nn de una cuadrícula de anchura 1 / 2n que intersecan al conjunto:
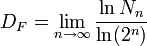
Se demuestra que ambas definiciones son equivalentes, y que son invariantes bajo isometrías.[6]
[editar] Dimensión de Hausdorff-Besicovitch
De una definición más compleja, la dimensión de Hausdorff-Besicovitch nos proporciona un número DH(A), también invariante bajo isometrías, cuya relación con la dimensión fractal DF(A) es la siguiente:
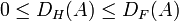
Esto permite distinguir en algunos casos entre conjuntos con la misma dimensión fractal.
[editar] Dimensión de fractales producidos por un IFS
En ese caso, cuando no haya solapamiento, se demuestra que DF = DH y que ambas pueden calcularse como solución de la ecuación:
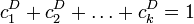
donde ci designa el factor de contracción de cada aplicación contractiva del IFS.
[editar] Aplicaciones
Se han utilizado técnicas de fractales en la compresión de datos y en diversas disciplinas científicas.
[editar] Compresión de imágenes
Comprimir la imagen de un objeto autosemejante como el helecho de la figura no es difícil: haciendo uso del teorema del collage, debemos encontrar un IFS, conjunto de transformaciones que lleva la figura completa (en negro) en cada una de sus partes autosemejantes (rojo, azul celeste y azul marino). La información sobre la imagen quedará codificada en el IFS, y la aplicación reiterada de dichas transformaciones permite obtener la imagen procesada en cuestión.
Pero el enfoque anterior plantea problemas con muchas imágenes reales: no esperamos, por ejemplo, que la imagen de un gato presente pequeños gatitos distorsionados sobre sí mismo. Para solventarlo, en 1989 Arnaud Jacquin creó el esquema de sistemas de funciones iteradas particionadas: en él se subdivide la imagen mediante una partición y para cada región resultante se busca otra región similar a la primera bajo las transformaciones apropiadas.[7]
El esquema resultante es un sistema de compresión con pérdidas, de tiempo asimétrico. Lamentablemente aún se tarda mucho en encontrar las transformaciones que definen la imagen. No obstante, una vez encontradas, la descodificación es muy rápida. La compresión, aunque dependa de muchos factores, suele ser equiparable a la compresión JPEG, con lo cual el factor tiempo resulta determinante para decantarse por uno u otro sistema.
[editar] Modelado de formas naturales

Fracción de un fractal Mandelbrot.
Las formas fractales, las formas en la que las partes se asemejan al todo, están presentes en la materia biológica, junto con las simetrías (las formas básicas que solo necesitan la mitad de información genética) y las espirales (Las formas de crecimiento y desarrollo de la forma básica hacia la ocupación de un mayor espacio), como las formas más sofisticadas en el desarrollo evolutivo de la materia biológica en cuanto que se presentan en procesos en los que se producen saltos cualitativos en las formas biológicas, es decir posibilitan catástrofes (hechos extraordinarios) que dan lugar a nuevas realidades más complejas, como las hojas que presentan una morfología similar a la pequeña rama de la que forman parte que, a su vez, presentan una forma similar a la rama, que a su vez es similar a la forma del árbol, y sin embargo cualitativamente no es lo mismo una hoja (forma biológica simple), que una rama o un árbol (forma biológica compleja).
[editar] Sistemas dinámicos
Pero además las formas fractales no sólo se presentan en las formas espaciales de los objetos sino que se observan en la propia dinámica evolutiva de los sistemas complejos (ver teoría del caos). Dinámica que consta de ciclos (en los que partiendo de una realidad establecida simple acaban en la creación de una nueva realidad más compleja) que a su vez forman parte de ciclos más complejos los cuales forman parte del desarrollo de la dinámica de otro gran ciclo. Las evoluciones dinámicas de todos estos ciclos presentan las similitudes propias de los sistemas caóticos.
[editar] En manifestaciones artísticas

Imagen generada con el programa Apophysis.
Se usan tanto en la composición armónica y rítmica de una melodía como en la síntesis de sonidos. Esto se debe al uso de lo que en composición se llaman "micromodos", o pequeños grupos de 3 notas, a partir de los cuales uno puede trabajarlos de manera horizontal (melódica), o vertical (armónica). A su vez, el ritmo puede ser trabajado en sucesiones temporales especificas, que son determinadas por sucesiones de fractales.
[editar] Literatura y poesía
Se usan también como punto de unión entre el arte y la ciencia, un ejemplo de eso es el científico-poeta chileno-alemán Mario Markus. En España, fue galardonado con el XI Premio de Poesía de la Academia de Poesía de Castilla y León, Fractalia, libro escrito por el poeta Carlos Escartín (Madrid, 1972), donde dedica este poemario a la exposición de cómo las Matemáticas y la Naturaleza están unidas desde el principio de los tiempos, y de cómo esto es posible actualmente verificarlo mediante el arte fractal, donde imágenes de la naturaleza (un copo de nieve, una hoja de un árbol) quedan perfectamente plasmadas en un plano, mediante la representación de puntos en el espacio realizados al aplicar algoritmos iterativos de números complejos.
[editar] Artes gráficas
Con programas informáticos como Apophysis o Ultra Fractal se pueden hacer imágenes con técnicas diversas; cambiando parámetros, geometría de triángulos o con transformaciones aleatorias (a veces llamadas "mutaciones").
[editar] Referencias
- ↑ Benoît Mandelbrot, La Geometría Fractal de la Naturaleza, Tusquets, ISBN 84-8310-549-7
- ↑ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Ltd.. pp. XXV. ISBN 0-470-84862-6.
- ↑ ¿Cuánto mide la costa de Gran Bretaña?
- ↑ Stewart, Ian. De aquí al infinito. Crítica, Grijalbo Mondadori, S.A., 1998. ISBN 84-7423-853-6.
- ↑ B. Mandelbrot. Los objetos fractales. Forma, azar y dimensión. Tusquets Editores, S.A., 1993. ISBN 978-84-7223-458-1
- ↑ Barnsley, M. Fractals everywhere.Academic Press Inc, 1988. ISBN 0-12-079062-9. (Cap 5)
- ↑ Jacquin, A.E.;Image coding based on a fractal theory of iterated contractive image transformations. Image Processing, IEEE Transactions on Volume 1, Issue 1, Jan. 1992 Page(s):18 - 30
[editar] Véase también
[editar] Enlaces externos
Arte fractal
Libros con licencia CC
Software
Vídeos
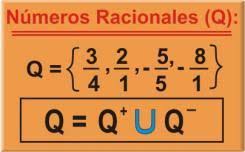
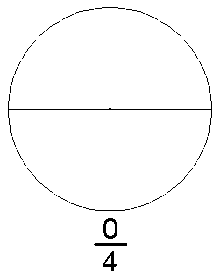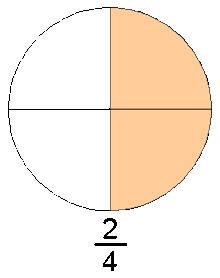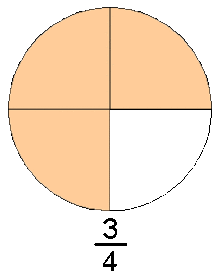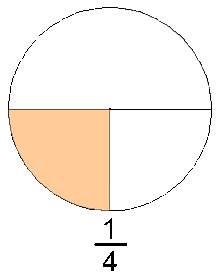
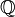 , que significa «cociente» (Quotient en varios idiomas europeos). Este conjunto de números incluye a los
, que significa «cociente» (Quotient en varios idiomas europeos). Este conjunto de números incluye a los 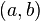 donde
donde 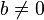 .
.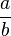 denota a
denota a 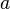 se le llama
se le llama 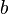 se le llama
se le llama 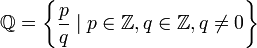
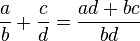
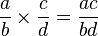

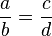 cuando
cuando 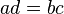
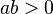
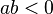
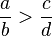 cuando
cuando 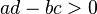
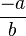 son denotados por
son denotados por 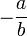
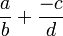 son denotadas por
son denotadas por 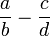
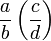 denota a
denota a 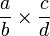
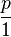 se denota simplemente por
se denota simplemente por 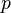 .
.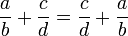
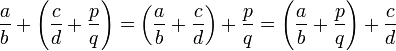
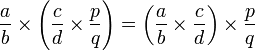
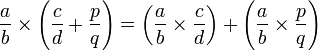
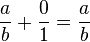 entonces
entonces  es el neutro aditivo de los racionales y se le denota por
es el neutro aditivo de los racionales y se le denota por 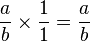 entonces
entonces  es el neutro multiplicativo de los racionales y se le denota por
es el neutro multiplicativo de los racionales y se le denota por 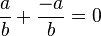
 tal que
tal que 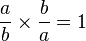
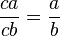 si
si 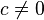 y
y 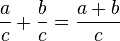
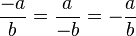
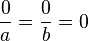 , a y b ≠ 0
, a y b ≠ 0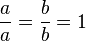 , a y b ≠ 0.
, a y b ≠ 0.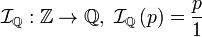
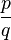 se puede expresar de forma única como
se puede expresar de forma única como 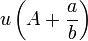 donde
donde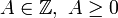
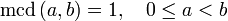
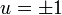
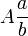 denota a
denota a 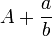
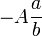 denota a
denota a 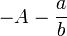
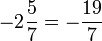
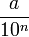
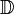 denota al conjunto de los números de este tipo. Es decir
denota al conjunto de los números de este tipo. Es decir 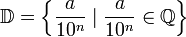
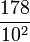 se denota como
se denota como 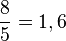
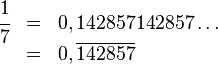
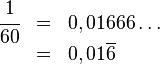
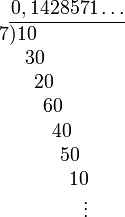
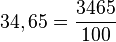
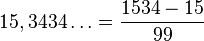
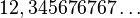 entonces
entonces 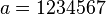 y
y 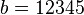 , por lo que el número buscado será
, por lo que el número buscado será 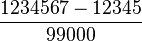 .
.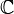
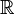
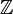
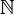















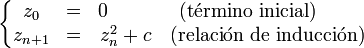
















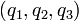 , variando una de ellas y manteniendo fijas las otras dos. Un sistema de coordenadas se dice ortogonal si las líneas coordenadas son ortogonales en cada punto. Las coordenadas cartesianas, las cilíndricas y las esféricas, son ejemplos de coordenadas ortogonales.
, variando una de ellas y manteniendo fijas las otras dos. Un sistema de coordenadas se dice ortogonal si las líneas coordenadas son ortogonales en cada punto. Las coordenadas cartesianas, las cilíndricas y las esféricas, son ejemplos de coordenadas ortogonales.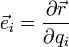

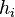 son los denominados factores de escala. Su nombre proviene de que dan la proporción entre lo que varía una coordenada y el desplazamiento que produce esta variación. De hecho el
son los denominados factores de escala. Su nombre proviene de que dan la proporción entre lo que varía una coordenada y el desplazamiento que produce esta variación. De hecho el ![[g_{ij}] = begin{bmatrix} h_{1}^{2} & 0 & 0 0 & h_{2}^{2} & 0 0 & 0 & h_{3}^{2} end{bmatrix}](https://petalofucsia.blogia.com/upload/externo-60f59ccc7dab4e677fa97f7704edd422.png)
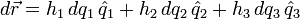
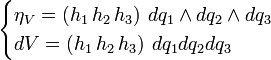
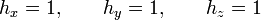
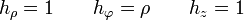
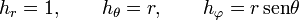













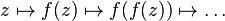 .
.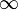 . Al conjunto de valores de
. Al conjunto de valores de 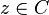 que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente
que no escapan al infinito mediante esta operación se le denomina conjunto de Julia relleno, y a su frontera, simplemente 


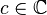 , se colorea de modo que refleje una propiedad básica del conjunto de Julia asociado a
, se colorea de modo que refleje una propiedad básica del conjunto de Julia asociado a 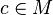 si el conjunto de Julia asociado a
si el conjunto de Julia asociado a