MATEMÁTICAS3: RAZÓN (MATEMÁTICAS). En matemáticas, una razón es una relación entre dos números semejantes (es decir, objetos, personas, estudiantes, cucharadas, unidades idénticas de cualquier dimensión), generalmente se expresa como "a es a b" o a:b, a veces se expresa aritméticamente como un cociente adimensional de los dos, que indica de manera explícita las veces que el primer número contiene el segundo.
Razón (matemáticas)
En matemáticas, una razón es una relación entre dos números semejantes (es decir, objetos, personas, estudiantes, cucharadas, unidades idénticas de cualquier dimensión), generalmente se expresa como "a es a b" o a:b, a veces se expresa aritméticamente como un cociente adimensional de los dos, que indica de manera explícita las veces que el primer número contiene el segundo.
Contenido[ocultar] |
[editar] Razón geométrica

La razón geométrica es la comparación de dos cantidades por su cociente, en donde se ve cuántas veces contiene una a la otra. Es necesario tener el dominio o rango para poder sacarla.
Ejemplo: 18 entre 6 es igual a 3 (18 tiene tres veces seis); su razón geométrica es 3.
La razón se puede escribir de 3 formas Ejemplo A. 50 sobre 70 B. 50 es a 70 C. 50: 70 El numerador de la razón se llama antecedente debido a que puede haberse dividido o multiplicado.
[editar] Razón aritmética
La razón aritmética de dos cantidades es la diferencia (o resta) de dichas cantidades. La razón aritmética se puede escribir colocando entre las dos cantidades el signo . o bien con el signo -. Así, la razón aritmética de 6 a 4 se escribe: 6.4 ó 6-4.
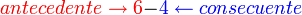
El primer término de una razón aritmética recibe el nombre de antecedente y el segundo el de consecuente. Así en la razón 6-4, el antecedente es 6 y el consecuente 4.
[editar] Propiedades de las razones Aritméticas
Como la razón aritmética de dos cantidades no es más que la resta indicada de dichas cantidades, las propiedades de las razones aritméticas serán las propiedades de toda suma o resta.
PRIMERA PROPIEDAD
Si al antecedente se le suma o resta una cantidad la razón aritmética queda aumentada o disminuida dicha cantidad.
- Primer caso (con la suma)
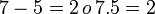
- Segundo caso (con la resta)
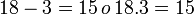
SEGUNDA PROPIEDAD
Si al consecuente de una razón aritmética se suma o se resta una cantidad cualquiera, la razón queda disminuida en el primer caso y aumentada en el segundo en la cantidad de veces que indica dicho número.
- Primer caso (sumando una cantidad cualquiera al consecuente)
- Segundo caso (restando una cantidad cualquiera al consecuente)
[editar] Proporciones Aritméticas
Una "proporción aritmética" es la = de 2 razones. Las proporciones aritméticas se pueden representar de dos maneras distintas:
- a/b = c/d o bien
- a:b = c:d
y se lee "a es a b como c es a d".
Los términos primero y cuarto de una proporción aritmética reciben el nombre de extremos, mientras que los términos segundo y tercero se denominan medios. Los términos primero y tercero reciben el nombre de antecedentes, mientras que los términos segundo y cuarto se llaman consecuentes.
Así sea la proporción aritmética 10:5 = 8:4. Los términos 10 y 4 (son extremos) y, 5 y 8 (son medios).
Las proporciones aritméticas cuyos medios no son iguales reciben el nombre de proporciones aritméticas discretas. Por el contrario, si los medios de la proporción aritmética son iguales, ésta recibe el nombre de continua. En el caso del ejemplo se trata de una proporción aritmética discreta porque sus medios son desiguales (5 y 8).
En toda proporción (no continua):
- El producto de los extremos será igual al producto de los medios.
(10×4 = 5×8)
Se define la media aritmética de una proporción aritmética continua como cada uno de los medios iguales de dicha proporción aritmética. Sea: 10-8::8-6. La media aritmética es 8.
La media aritmética de una proporción aritmética es igual a la semisuma de los extremos.
La razón geométrica de dos números es el cociente exacto de dividir el primero a por el segundo b y se representa:
a:bSe lee "a" es a "b" como "c" es a "d"
Donde el a, b son entero, fraccionario o mixto (desde el punto de la aritmética).
Las razones se pueden escribir de tres maneras diferentes:
Ejemplo:
2 es a 202:1 /12/1Por lo tanto toda razón se puede expresar como una fracción y eventualmente como un decimal.

3 comentarios
petalofucsia -
petalofucsia -
LA HISTORIA, SÍ, ERAN TODO RAZONES.
petalofucsia -
LA HISTORIA SE DETENÍA EN ALGUNAS COSAS COMO PARA VERIFICAR QUE ESTABAN CORRECTAS.
LA HISTORIA ERA TODO RAZONES Y MÁS RAZONES PARA TODO.
CON EL PENSAMIENTO RESULTABA SENCILLO RAZONAR LO QUE SE NOS PREGUNTABA, RECOGIDO TODO EN EL CÓDICE CALIXTINUS.