MATEMÁTICAS3: SUPREMOS. En matemáticas, dado un subconjunto S de un conjunto parcialmente ordenado (P,

30 de noviembre de 2010 - 18:06 - Matemáticas3

Supremo

De Wikipedia, la enciclopedia libre

Un conjunto A de números reales (representados por círculos azules), un conjunto de cotas superiores de A (círculos rojos), y el mínimo de las cotas superiores, el supremo de A(diamante rojo).

En matemáticas, dado un subconjunto S de un conjunto parcialmente ordenado (P, <), el supremo de S, si existe, es el mínimo elemento de P que es mayor o igual a cada elemento de S. En otras palabras, es la mínima de las cotas superiores de S. El supremo de un conjunto S comumente se denota sup(S).

[editar] Propiedades

Si el supremo existe, entonces es único
$sup(A cup B)= max{sup(A),sup(B)}$ , si es que dichos supremos existen
Un conjunto tiene máximo, si y solo si contiene a su supremo

[editar] Ejemplos

En el campo de los números reales, todo subconjunto no vacio, acotado superiormente tiene supremo.
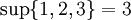
$sup { 1, 2, 3 } = 3,$
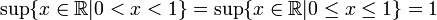
$sup { x in mathbb{R} | 0 < x < 1 } = sup { x in mathbb{R} | 0 leq x leq 1 } = 1,$
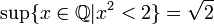
$sup { x in mathbb{Q} | x^2 < 2 } = sqrt{2},$
$sup { (-1)^n - frac{1}{n} | n in mathbb{N} } = 1,$