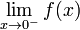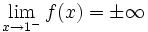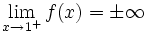De Wikipedia, la enciclopedia libre
En general el término cálculo (del latín calculus = piedra)[1] hace referencia, indistintamente, a la acción o el resultado correspondiente a la acción de calcular. Calcular, por su parte, consiste en realizar las operaciones necesarias para prever el resultado de una acción previamente concebida, o conocer las consecuencias que se pueden derivar de unos datos previamente conocidos.
No obstante, el uso más común del término cálculo es el lógico-matemático. Desde esta perspectiva, el cálculo consiste en un procedimiento mecánico, o algoritmo, mediante el cual podemos conocer las consecuencias que se derivan de unos datos previamente conocidos.
Cálculo como razonamiento y cálculo lógico-matemático
Las dos acepciones del cálculo (la general y la restringida) arriba definidas están íntimamente ligadas. El cálculo es una actividad natural y primordial en el hombre, que comienza en el mismo momento en que empieza a relacionar unas cosas con otras en un pensamiento o discurso. El cálculo lógico natural como razonamiento es el primer cálculo elemental del ser humano. El cálculo en sentido lógico-matemático aparece cuando se toma conciencia de esta capacidad de razonar y trata de formalizarse.
Por lo tanto, podemos distinguir dos tipos de operaciones:
- Operaciones orientadas hacia la consecución de un fin, como prever, programar, conjeturar, estimar, precaver, prevenir, proyectar, configurar, etc. que incluyen en cada caso una serie de complejas actividades y habilidades tanto de pensamiento como de conducta. En su conjunto dichas actividades adquieren la forma de argumento o razones que justifican una finalidad práctica o cognoscitiva.
- Operaciones formales como algoritmo que se aplica bien directamente a los datos conocidos o a los esquemas simbólicos de la interpretación lógico-matemática de dichos datos; las posibles conclusiones, inferencias o deducciones de dicho algoritmo son el resultado de la aplicación de reglas estrictamente establecidas de antemano.
Resultado que es:
Conclusión de un proceso de razonamiento.Resultado aplicable directamente a los datos iniciales (resolución de problemas).
Modelo de relaciones previamente establecido como teoría científica y significativo respecto a determinadas realidades (Creación de modelos científicos).Mero juego formal simbólico de fundamentación, creación y aplicación de las reglas que constituyen el sistema formal del algoritmo (Cálculo lógico-matemático, propiamente dicho).
Dada la importancia que históricamente ha adquirido la actividad lógico-matemática en la cultura humana el presente artículo se refiere a este último sentido. De hecho la palabra, en su uso habitual, casi queda restringida a este ámbito de aplicación; para algunos, incluso, queda reducida a un solo tipo de cálculo matemático, pues en algunas universidades se llamaba "Cálculo" a una asignatura específica de cálculo matemático.
En un artículo general sobre el tema no puede desarrollarse el contenido de lo que supone el cálculo lógico-matemático en la actualidad. Aquí se expone solamente el fundamento de sus elementos más simples, teniendo en cuenta que sobre estas estructuras simples se construyen los cálculos más complejos tanto en el aspecto lógico como en el matemático.
Historia del cálculo
De la Roma Clásica a la Edad Media

Reconstrucción de un
ábaco romano.
El término "cálculo" procede del latín calculus, piedrecita que se mete en el calzado y que produce molestia. Precisamente tales piedrecitas ensartadas en tiras constituían el ábaco romano que, junto con el suwanpan japonés, constituyen las primeras máquinas de calcular en el sentido de contar.
Los antecedentes de procedimiento de cálculo, como algoritmo, se encuentran en los que utilizaron los geómetras griegos, Eudoxo en particular, en el sentido de llegar por aproximación de restos cada vez más pequeños, a una medida de figuras curvas; así como Diofanto precursor del álgebra.
La consideración del cálculo como una forma de razonamiento abstracto aplicado en todos los ámbitos del conocimiento se debe a Aristóteles, quien en sus escritos lógicos fue el primero en formalizar y simbolizar los tipos de razonamientos categóricos (silogismos). Este trabajo sería completado más tarde por los estoicos, los megáricos, la Escolástica.
El algoritmo actual de cálculo aritmético como universal es fruto de un largo proceso histórico a partir de las aportaciones de Muhammad ibn al-Juarismi en el siglo IX.[2]
Se introdujo el 0, ya de antiguo conocido en la India y se construye definitivamente el sistema decimal de diez cifras con valor posicional de las mismas, introducido en Europa por los árabes. La escritura antigua de números en Babilonia, en Egipto, en Grecia o en Roma, hacía muy difícil un procedimiento mecánico de cálculo.[3]
El sistema decimal fue muy importante para el desarrollo de la contabilidad de los comerciantes de la Baja Edad Media, en los inicios del capitalismo.
El concepto de función por tablas ya era practicado de antiguo pero adquirió especial importancia en la Universidad de Oxford en el siglo XIV.[4] La idea de un lenguaje o algoritmo capaz de determinar todas las verdades, incluidas las de la fe, aparecen en el intento de Raimundo Lulio en su Ars Magna
A fin de lograr una operatividad mecánica se confeccionaban unas tablas a partir de las cuales se podía generar un algoritmo prácticamente mecánico. Este sistema de tablas ha perdurado en algunas operaciones durante siglos, como las tablas de logaritmos, o las funciones trigonométricas; las tablas venían a ser como la calculadora de hoy día; un instrumento imprescindible de cálculo. Las amortizaciones de los créditos en los bancos, por ejemplo, se calculaban a partir de tablas elementales hasta que se produjo la aplicación de la informática en el tercer tercio del siglo XX.
A finales de la Edad Media la discusión entre los partidarios del ábaco y los partidarios del algoritmo se decantó claramente por estos últimos.[5] De especial importancia es la creación del sistema contable por partida doble inventado por Luca Pacioli fundamental para el progreso del capitalismo en el Renacimiento.[6]
Renacimiento
Ejemplo de aplicación de un cálculo algebraico a la resolución de un problema según la interpretación de una teoría física
La expresión del cálculo algebraico y = xt, indica las relaciones sintácticas que existen entre tres variables que no tienen significado alguno. Pero si interpretamos y como espacio, x como velocidad y t como tiempo, tal ecuación modeliza una teoría física que establece que el espacio recorrido por un móvil con velocidad constante es directamente proporcional a la velocidad con que se mueve y al tiempo que dura su movimiento.Al mismo tiempo, según dicha teoría, sirve para resolver el problema de calcular cuántos kilómetros ha recorrido un coche que circula de Madrid a Barcelona a una velocidad constante de 60 km/h durante 4 horas de recorrido.- 240 kilómetros recorridos = 60 km x 4 h
|
El sistema que usamos actualmente fue introducido por Luca Pacioli en 1494, y fue creado y desarrollado para responder a la necesidad de la contabilidad en los negocios de la burguesía renacentista.
El desarrollo del álgebra (con la introducción de un sistema de símbolos por un lado, y la resolución de problemas por medio de las ecuaciones) vino de la mano de los grandes matemáticos renacentistas como Tartaglia, Stévin, Cardano o Vieta y fue esencial para el planteamiento y solución de los más diversos problemas que surgieron en la época como consecuencia de los grandes descubrimientos que hicieron posible el progreso científico que surgirá en el siglo XVII.[7]
Siglos XVII y XVIII

Página del artículo de
Leibniz "Explication de l'Arithmétique Binaire", 1703/1705.
En el siglo XVII el cálculo conoció un enorme desarrollo siendo los autores más destacados Descartes,[8] Pascal[9] y, finalmente, Leibniz y Newton[10] con el cálculo infinitesimal que en muchas ocasiones ha recibido simplemente, por absorción, el nombre de cálculo.
El concepto de cálculo formal en el sentido de algoritmo reglado para el desarrollo de un razonamiento y su aplicación al mundo de lo real[11] adquiere una importancia y desarrollo enorme respondiendo a una necesidad de establecer relaciones matemáticas entre diversas medidas, esencial para el progreso de la ciencia física que, debido a esto, es tomada como nuevo modelo de Ciencia frente a la especulación tradicional filosófica, por el rigor y seguridad que ofrece el cálculo matemático. Cambia así el sentido tradicional de la Física como Ciencia de la Naturaleza y toma el sentido de ciencia que estudia los cuerpos materiales, en cuanto materiales.
A partir de entonces el propio sistema de cálculo permite establecer modelos sobre la realidad física, cuya comprobación experimental[12] supone la confirmación de la teoría como sistema. Es el momento de la consolidación del llamado método científico cuyo mejor exponente es en aquel momento la Teoría de la Gravitación Universal y las leyes de la Mecánica de Newton.[13]
Siglos XIX y XX
Durante el siglo XIX y XX el desarrollo científico y la creación de modelos teóricos fundados en sistemas de cálculo aplicables tanto en mecánica como en electromagnetismo y radioactividad, etc. así como en astronomía fue impresionante. Las geometrías no euclidianas encuentran aplicación en modelos teóricos de astronomía y física. El mundo deja de ser un conjunto de infinitas partículas que se mueven en un espacio-tiempo absoluto y se convierte en un espacio de configuración o espacio de fases de n dimensiones que físicamente se hacen consistentes en la teoría de la relatividad, la mecánica cuántica, la teoría de cuerdas etc. que cambia por completo la imagen del mundo físico.
La lógica asimismo sufrió una transformación radical.[14] La formalización simbólica fue capaz de integrar las leyes lógicas en un cálculo matemático, hasta el punto que la distinción entre razonamiento lógico-formal y cálculo matemático viene a considerarse como meramente utilitaria.
En la segunda mitad del siglo XIX y primer tercio del XX, a partir del intento de formalización de todo el sistema matemático, Frege, y de matematización de la lógica, (Bolzano, Boole, Whitehead, Russell) fue posible la generalización del concepto como cálculo lógico. Se lograron métodos muy potentes de cálculo, sobre todo a partir de la posibilidad de tratar como “objeto” conjuntos de infinitos elementos, dando lugar a los números transfinitos de Cantor.
Mediante el cálculo la lógica encuentra nuevos desarrollos como lógicas modales y lógicas polivalentes.
Los intentos de axiomatizar el cálculo como cálculo perfecto por parte de Hilbert y Poincaré, llevaron, como consecuencia de diversas paradojas (Cantor, Russell etc.) a nuevos intentos de axiomatización, Axiomas de Zermelo-Fraenkel y a la demostración de Gödel de la imposibilidad de un sistema de cálculo perfecto: consistente, decidible y completo en 1931, de grandes implicaciones lógicas, matemáticas y científicas.
Actualidad
En la actualidad, el cálculo en su sentido más general, en tanto que cálculo lógico interpretado matemáticamente como sistema binario, y físicamente hecho material mediante la lógica de circuitos eléctrónicos, ha adquirido una dimensión y desarrollo impresionante por la potencia de cálculo conseguida por los ordenadores, propiamente máquinas computadoras. La capacidad y velocidad de cálculo de estas máquinas hace lo que humanamente sería imposible: millones de operaciones por segundo.
El cálculo así utilizado se convierte en un instrumento fundamental de la investigación científica por las posibilidades que ofrece para la modelización de las teorías científicas, adquiriendo especial relevancia en ello el cálculo numérico.
Concepto general de cálculo
El cálculo es un sistema de símbolos no interpretados, es decir, sin significado alguno, en el que se establecen mediante reglas estrictas, las relaciones sintácticas entre los símbolos para la construcción de fórmulas bien formadas (fbf), así como las reglas que permiten transformar dichas expresiones en otras equivalentes; entendiendo por equivalentes que ambas tienen siempre y de forma necesaria el mismo valor de verdad. Dichas transformaciones son meramente tautologías.
Un cálculo consiste en:
- Un conjunto de elementos primitivos. Dichos elementos pueden establecerse por enumeración, o definidos por una propiedad tal que permita discernir sin duda alguna cuándo un elemento pertenece o no pertenece al sistema.
- Un conjunto de reglas de formación de “expresiones bien formadas”(EBFs) que permitan en todo momento establecer, sin forma de duda, cuándo una expresión pertenece al sistema y cuándo no.
- Un conjunto de reglas de transformación de expresiones, mediante las cuales partiendo de una expresión bien formada del cálculo podremos obtener una nueva expresión equivalente y bien formada que pertenece al cálculo.
Cuando en un cálculo así definido se establecen algunas expresiones determinadas como verdades primitivas o axiomas, decimos que es un sistema formal axiomático.
Un cálculo así definido si cumple al mismo tiempo estas tres condiciones decimos que es un Cálculo Perfecto:
- Es consistente: No es posible que dada una expresión bien formada del sistema, f, y su negación, no − f, sean ambas teoremas del sistema. No puede haber contradicción entre las expresiones del sistema.
- Decidible: Dada cualquier expresión bien formada del sistema podemos encontrar un método que nos permita decidir mediante una serie finita de operaciones si dicha expresión es o no es un teorema del sistema.
- Completo: Cuando dada cualquier expresión bien formada del sistema, podemos establecer la demostración o prueba de que es un teorema del sistema.
La misma lógica-matemática ha demostrado que tal sistema de cálculo perfecto "no es posible" (véase el Teorema de Gödel).
El cálculo lógico
Entendemos aquí por cálculo lógico, un algoritmo que permite cómoda y fácilmente inferir o deducir un enunciado verdadero a partir de otro u otros que se tienen como válidamente verdaderos.
La inferencia o deducción es una operación lógica que consiste en obtener un enunciado como conclusión a partir de otro(s) (premisas) mediante la aplicación de reglas de inferencia.[15]
Decimos que alguien infiere -o deduce- "T" de "R" si acepta que si "R" tiene valor de verdad V, entonces, necesariamente, "T" tiene valor de verdad V.
Los hombres en nuestra tarea diaria, utilizamos constantemente el razonamiento deductivo. Partimos de enunciados empíricos -supuestamente verdaderos y válidos- para concluir en otro enunciado que se deriva de aquellos, según las leyes de la lógica natural.[16]
La lógica, como ciencia formal, se ocupa de analizar y sistematizar dichas leyes, fundamentarlas y convertirlas en las reglas que permiten la transformación de unos enunciados -premisas- en otros -conclusiones- con objeto de convertir las operaciones en un algoritmo riguroso y eficaz, que garantiza que dada la verdad de las premisas, la conclusión es necesariamente verdadera.
Al aplicar las reglas de este cálculo lógico a los enunciados que forman un argumento mediante la simbolización adecuada de fórmulas o Expresiones bien formadas (EBF) construimos un modelo o sistema deductivo.
Sistematización de un cálculo de deducción natural
Reglas de formación de fórmulas
I. Una letra enunciativa (con o sin subíndice) es una EBF.
II. Si A es una EBF, ¬ A también lo es.
III. Si A es una EBF y B también, entonces A 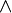 B; A
B; A 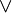 B; A
B; A 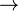 B; A
B; A 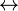 B, también lo son.
B, también lo son.
IV. Ninguna expresión es una fórmula del Cálculo sino en virtud de I,II,III.
Notas:
- A, B,... con mayúsculas están utilizadas como metalenguaje en el que cada variable expresa cualquier proposición, atómica (p,q,r,s....) o molecular (p/q), (p/q)...
- A, B,... son símbolos que significan variables; ¬,
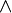 ,
, 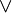 , →,
, →, 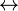 , son símbolos constantes.
, son símbolos constantes. - Existen diversas formas de simbolización. Utilizamos aquí la de uso más frecuente en España.[17]
Reglas de transformación de fórmulas
1) Regla de sustitución (R.T.1):
Dada una tesis EBF del cálculo, en la que aparecen variables de enunciados, el resultado de sustituir una, algunas o todas esas variables por expresiones bien formadas (EBF) del cálculo, será también una tesis EBF del cálculo. Y ello con una única restricción, si bien muy importante: cada variable ha de ser sustituida siempre que aparece y siempre por el mismo sustituto.
Veamos el ejemplo:
| 1 | ![left [ left ( p land q right ) lor r right ]rightarrow t lor s](https://petalofucsia.blogia.com/upload/externo-cd43ae6ff74778d241c947e695d41d7c.png) | Transformación |
| 2 | 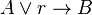 | donde 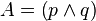 ; y donde ; y donde 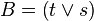 |
| 3 | 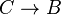 | donde 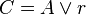 |
O viceversa
| 1 | 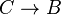 | Transformación |
| 2 | 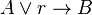 | donde 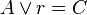 |
| 3 | ![left [ left ( p land q right ) lor r right ]rightarrow t lor s](https://petalofucsia.blogia.com/upload/externo-cd43ae6ff74778d241c947e695d41d7c.png) | donde 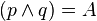 ; y donde ; y donde 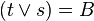 |
2) Regla de separación (R.T.2):
Si X es una tesis EBF del sistema y lo es también X 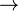 Y, entonces Y es una tesis EBF del sistema.
Y, entonces Y es una tesis EBF del sistema.
Esquemas de inferencia
Sobre la base de estas dos reglas, siempre podremos reducir un argumento cualquiera a la forma:
![[A land B land C....land N]rightarrow Y](https://petalofucsia.blogia.com/upload/externo-c736b8c23ddc520a6b1f4252e48d8428.png)
lo que constituye un esquema de inferencia en el que una vez conocida la verdad de cada una de las premisas A, B,...N y, por tanto, de su producto, podemos obtener la conclusión Y con valor de verdad V, siempre y cuando dicho esquema de inferencia sea una ley lógica, es decir su tabla de verdad nos muestre que es una tautología.
Por la regla de separación podremos concluir Y, de forma independiente como verdad.
Dada la poca operatividad de las tablas de verdad, el cálculo se construye como una cadena deductiva aplicando a las premisas o a los teoremas deducidos las leyes lógicas utilizadas como reglas de transformación, como se expone en cálculo lógico.
Cuando en un Cálculo C, se establece una "correspondencia" de cada símbolo con elementos determinados individuales distinguibles entre sí, de un Universo L, real, (tal universo L no es un conjunto vacío, por las mismas condiciones que hemos establecido) ENTONCES se dice que L es un MODELO de C.
El lenguaje natural como modelo de un cálculo lógico
Naturalmente el cálculo lógico es útil porque puede tener aplicaciones, pero ¿en qué consisten o cómo se hacen tales aplicaciones?
Podemos considerar que el lenguaje natural es un modelo de C si podemos someterlo, es decir, aplicarle una correspondencia en C.
Para ello es necesario someter al lenguaje natural a un proceso de formalización de tal forma que podamos reducir las expresiones lingüísticas del lenguaje natural a EBFs de un cálculo mediante reglas estrictas manteniendo el sentido de verdad lógica de dichas expresiones del lenguaje natural. Esto es lo que se expone en cálculo lógico.
Las diversas formas en que tratemos las expresiones lingüísticas dan lugar a sistemas diversos de formalización y cálculo:
- Cálculo proposicional o cálculo de enunciados
Cuando se toma la oración simple significativa del lenguaje natural con posible valor de verdad o falsedad como una
proposición atómica, como un todo sin analizar.
La oración simple: "Llueve", o "Las farolas se apagan por la noche" son consideradas como posible valor de verdad o falsedad de una variable "p".
- Cálculo como lógica de clases
Cuando se toma la oración simple significativa del lenguaje natural con posible valor de verdad o falsedad como resultado del análisis de la oración como una relación de individuos o posibles individuos que pertenecen o no pertenecen a una
clase.Siendo una clase el
criterio, como una
propiedad o una
definición, que permite
ordenar a todos los posibles individuos de un
Universo determinado como pertenecientes o no pertenecientes a dicha clase. La clase como
propiedad o
definición define al conjunto de
posibles individuos, pero es independiente de la existencia de dichos individuos; no se identifica con el conjunto de individuos. Clase = Pegaso; Propiedad o definición = Caballo con alas; Individuos = ninguno.Esta es la forma en la que en la actualidad se interpreta la lógica
silogística de Aristóteles, que queda así se reducida a un cálculo según la
lógica de clases.
La oración simple "Todos los caballos corren por el campo" está analizada como: La clase de todos los posibles seres que corren por el campo (B) incluye a la clase formada por todos los posibles seres que sean caballos (A).
- Cálculo de predicados o cuantificacional
Cuando se toma la oración simple significativa del lenguaje natural con posible valor de verdad o falsedad como resultado del análisis de la misma de forma que una posible función predicativa (P), se predica de unos posibles sujetos variables (x)
[tomados en toda su posible extensión: (Todos los x); o referente a algunos indeterminados: (algunos x)], o de una constante individual existente (a).
La oración simple "los perros muerden" se formaliza de la siguiente manera:
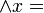 Todos los posibles perros;
Todos los posibles perros;
P = todas las posibles acciones de morder.
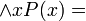 Para todo x (siendo x un perro) x muerde = Todos los perros muerden.
Para todo x (siendo x un perro) x muerde = Todos los perros muerden.
En el caso de Desko que es mi perro al que simbolizo como una constante a:
P(a) = Mi perro Desko muerde.
- Cálculo como lógica de relaciones
Cuando se toma la oración simple significativa con posible valor de verdad propio, verdado o falso, como resultado del análisis de la oración como una relación "R" que se establece entre un sujeto y un predicado.
Así la oración simple "Antonio es mayor que Pedro", se considera y simboliza bajo la relación "ser mayor que" (R) que se da entre Antonio (a) y Pedro (p) y se simboliza como aRp.
La simbolización y formación de EBFs en cada uno de esos cálculos, así como las reglas de cálculo se trata en cálculo lógico.
Cálculos matemáticos
Cálculo aritmético
Aritmética es la rama de las matemáticas que estudia ciertas operaciones de los números y sus propiedades elementales. Proviene del griego arithmos y techne que quieren decir respectivamente números y habilidad.
El número en aritmética elemental tiene la consideración de número natural referido, en el campo de la experiencia, a la unidad, entendida bien como cantidad bien como medida.
De hecho el cálculo más natural y primitivo surge de la necesidad de contar y medir.[18] Pero las formas y modos para realizar el cálculo han surgido según las diversas formas de sistemas de numeración, así como su transcripción gráfica.
Algoritmos
Sistema numérico y sistema de numeración
El sistema de numeración decimal, considerado como universal en la utilización más corriente, es un sistema posicional con base en 10 elementos o cifras (0, 1, 2, 3, 4, 5, 6, 7, 8, 9),[19] que adquieren un valor posicional a la hora de determinar el número.
Las posiciones se inician por la derecha: La primera indica las unidades; la segunda las decenas; la tercera las centenas; la cuarta el millar; siendo cada cifra a la izquiera tantas unidades de la potencia de 10 que corresponda al número de la posición.[20]
El número 7452: Se lee: Siete mil cuatrocientos cincuenta y dos. Y consta de 7 unidades de mil (7 unidades de millar; millar = 10³), 4 de cien (4 unidades de centenas; centena = 10²), 5 de 10 (5 unidades de decenas; decena = 10) y 2 unidades.
Operaciones básicas del cálculo: suma, resta, multiplicación y división
Las cuatro operaciones suma, resta, multiplicación y división son las operaciones básicas del cálculo, sobre las cuales se construyen todas las demás. Es lo que se enseña en la Escuela Primaria y se conoce como "Las cuatro reglas" y es considerado como la mínima expresión de un conocimiento básico.
1. Algoritmo de la Suma
El algoritmo se construye a partir de unas tablas elementales. La operación de suma consiste en la unión de las unidades contenidas en dos números, "sumandos", siendo el resultado la "Suma". Las tablas se leen como "una y una dos".
2. Algoritmo de la resta
Artículo principal: Resta El algoritmo se construye a partir de unas tablas elementales. La operación de resta se considera como la diferencia entre dos números, uno mayor "Minuendo" y otro menor "Sustraendo", siendo el resultado "Resta". Las tablas se leen como "de tres a cinco 2".
3. Algoritmo de la multiplicación

Una multiplicación de ejemplo
La multiplicación es una suma reiterativa de un mismo número, el "multiplicando", tantas veces como unidades tenga otro número, el "multiplicador". El algoritmo se construye a partir de unas tablas elementales. "Que se leen "una por una es 1"; "cinco por cuatro veinte" etc.(véase el artículo Tabla de multiplicar)
4. Algoritmo de la división
La operación se realiza entre dos números, "dividendo" y "divisor", cuyo resultado expresa cuántas veces se encuentra contenido el divisor en el dividendo. Equivale a medir el dividendo tomando como unidad el divisor. El resultado se llama "cociente", y las unidades no divisibles se denominan "resto". Operacionalmente consiste en ir restando sucesivamente el divisor al dividendo hasta que finalmente quede un resto menor que el divisor. El algoritmo se construye a partir de unas tablas elementales que se leen: "una entre una a una".
Algoritmo de potencias y raíces

Algoritmo de la raíz cuadrada
Potencias
Por potencia se entiende el resultado de multiplicar un mismo número, llamado "base", tantas veces como indica un índice o "exponente".
Se representa como bn, donde b es la base y n el exponente.
Así: 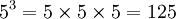
El algoritmo de cálculo de una potencia, aplicando las tablas de multiplicar sucesivamente y su algoritmo no ofrecen problema alguno.
Raíces
Mayor dificultad ofrece el cálculo de raíces, exponiendo como caso elemental, el algoritmo de la raíz cuadrada.
La raíz es la operación inversa de la potencia. Se expresa ![sqrt[n]{x}](https://petalofucsia.blogia.com/upload/externo-3f61efd698b7851c132bb6cec4fe04ee.png) donde x se llama "radicando" y n "raiz", y se trata de calcular un número y tal que yn + r = x siendo r un resto, si lo hubiera, por no ser la raíz exacta.
donde x se llama "radicando" y n "raiz", y se trata de calcular un número y tal que yn + r = x siendo r un resto, si lo hubiera, por no ser la raíz exacta.
Este algoritmo de cálculo aritmético está en desuso desde la introducción de las calculadoras electrónicas en el ambiente educativo.
2. Cálculo algebraico
3. Cálculo infinitesimal: breve reseña
El cálculo infinitesimal, llamado por brevedad "cálculo", tiene su origen en la antigua geometría griega. Demócrito calculó el volumen de pirámides y conos considerándolos formados por un número infinito de secciones de grosor infinitesimal (infinitamente pequeño). Eudoxo y Arquímedes utilizaron el "método de agotamiento" o exhaución para encontrar el área de un círculo con la exactitud finita requerida mediante el uso de polígonos regulares inscritos de cada vez mayor número de lados. En el periodo tardío de Grecia, el neoplatónico Pappus de Alejandría hizo contribuciones sobresalientes en este ámbito. Sin embargo, las dificultades para trabajar con números irracionales y las paradojas de Zenón de Elea impidieron formular una teoría sistemática del cálculo en el periodo antiguo.
En el siglo XVII, Cavalieri y Torricelli ampliaron el uso de los infinitesimales, Descartes y Fermat utilizaron el álgebra para encontrar el área y las tangentes (integración y Derivación en términos modernos). Fermat y Barrow tenían la certeza de que ambos cálculos estaban relacionados, aunque fueron Newton (hacia 1660), en Inglaterra y Leibniz en Alemania (hacia 1670) quienes demostraron que los problemas del área y la tangente son inversos, lo que se conoce como teorema fundamental del cálculo.
El descubrimiento de Newton, a partir de su teoría de la gravitación universal, fue anterior al de Leibniz, pero el retraso en su publicación aún provoca controversias sobre quién de los dos fue el primero. Newton utilizó el cálculo en mecánica en el marco de su tratado "Principios matemáticos de filosofía natural", obra científica por excelencia, llamando a su método de "fluxiones". Leibniz utilizó el cálculo en el problema de la tangente a una curva en un punto, como límite de aproximaciones sucesivas, dando un carácter más filosófico a su discurso. Sin embargo, terminó por adoptarse la notación de Leibniz por su versatilidad.
En el siglo XVIII aumentó considerablemente el número de aplicaciones del cálculo, pero el uso impreciso de las cantidades infinitas e infinitesimales, así como la intuición geométrica, causaban todavía confusión y duda sobre sus fundamentos. De hecho, la noción de límite, central en el estudio del cálculo, era aun vaga e imprecisa en ese entonces. Uno de sus críticos más notables fue el filósofo George Berkeley.
En el siglo XIX el trabajo de los analistas matemáticos sustituyeron esas vaguedades por fundamentos sólidos basados en cantidades finitas: Bolzano y Cauchy definieron con precisión los conceptos de límite en términos de épsilon_delta y de derivada, Cauchy y Riemann hicieron lo propio con las integrales, y Dedekind y Weierstrass con los números reales. Fue el periodo de la fundamentación del cálculo. Por ejemplo, se supo que las funciones diferenciables son continuas y que las funciones continuas son integrables, aunque los recíprocos son falsos. En el siglo XX, el análisis no convencional, legitimó el uso de los infinitesimales, al mismo tiempo que la aparición de las Computadoras ha incrementado las aplicaciones y velocidad del cálculo.
Actualmente, el cálculo infinitesimal tiene un doble aspecto: por un lado, se ha consolidado su carácter disciplinario en la formación de la sociedad culta del conocimiento, destacando en este ámbito textos propios de la disciplina como el de Louis Leithold, el de Earl W. Swokowski o el de James Stewart entre muchos otros; por otro su desarrollo como disciplina científica que ha desembocado en ámbitos tan especializados como el cálculo fraccional, la teoría de funciones analíticas de variable compleja o el análisis matemático. El éxito del cálculo ha sido extendido con el tiempo a las ecuaciones diferenciales, al cálculo de vectores, al cálculo de variaciones, al análisis complejo y a las topología algebraica y topología diferencial entre muchas otras ramas.
El desarrollo y uso del cálculo ha tenido efectos muy importantes en casi todas las áreas de la vida moderna: es fundamento para el cálculo numérico aplicado en casi todos los campos técnicos y/o científicos cuya principal característica es la continuidad de sus elementos, en especial en la física. Prácticamente todos los desarrollos técnicos modernos como la construcción, aviación, transporte, meteorología, etc. hacen uso del cálculo. Muchas fórmulas algebraicas se usan hoy en día en balística, calefacción, refrigeración, etc.
Como complemento del cálculo, en relación a sistemas teóricos o físicos cuyos elementos carecen de continuidad, se ha desarrollado una rama especial conocida como Matemática discreta.
Véase también
Referencias
- ↑ La palabra castellana cálculo se deriva del latín calculus que significa piedra, ya que se utilizaban guijarros para auxiliarse en la resolución de los problemas de cálculo aritmético, para contar y realizar las operaciones aritméticas elementales. En medicina las piedras de la vesícula o del riñón se llaman cálculos
- ↑ La palabra algoritmo se introdujo en matemáticas en honor a este matemático árabe.
- ↑ Muy interesante la descripción de este proceso en Cifra (matemática)
- ↑ Ver lógica empírica
- ↑ Sacrobosco, Algoritmos 1488; Georg von Peurbach, Algorithmus, 1492; Luca Pacioli; Summa de Arithmetica proportioni et porportionalita, 1494. Muy interesante y divertida exposición de esta guerra en Cifra (matemática)
- ↑ Sombart W.: El burgués:Contribución a la historia espiritual del hombre económico moderno. 1979. Madrid. Alianza
- ↑ La brújula y las grandes rutas marítimas, con el descubrimiento de América; la transformación de la guerra por la aplicación de la pólvora, que suscita el interés por el estudio del movimiento de los proyectiles Tartaglia;la aceptación del préstamo con interés y la creación de las sociedades por acciones que iniciaron el primer gran capitalismo; la nuevas tablas astronómicas sustituyendo las tablas alfonsinas (Tycho Brahe); y el copernicanismo que rompe la imagen medieval del mundo
- ↑ Que llega a concebir el mundo como racional sometido a una mathesis universal, la extensión, que convierte el mundo material en un inmenso mecanismo, teoría mecanicista, perfectamente calculable según un orden matemático que surge del análisis concebido como método de investigación.
- ↑ Cálculo de cónicas, estudio mecánico de las presiones, principio de Pascal de enorme importancia en la hidroestática, y finalmente en el cálculo de probabilidades.
- ↑ Con su famosa polémica acerca de la invención del cálculo infinitesimal de tanta importancia y que parece comprobado ser producto independiente de cada uno de ellos
- ↑ Cálculo de movimientos como el de caída libre de los graves, Galileo,; trayectoria de los planetas, Kepler; trayectoria de proyectiles para la artillería; medidas astronómicas y geográficas; presiones, Torricelli y Pascal; y todas las aplicaciones prácticas de estos cálculos para la práctica de la navegación y la naciente industria: bombas de vacío, prensa hidráulica, electricidad, magnetismo etc.
- ↑ Véase en Lógica empírica su aplicación por Galileo al movimiento de caída libre de los graves.
- ↑ El modelo de Newton se basa en una geometría analítica espacial de tres dimensiones inmutables como espacio absoluto y una sucesión constante e inmutable en una dirección de tiempo absoluto en los que una infinidad de partículas materiales masas se mueven según un principio universal la Gravitación Universal
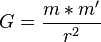 , y unas leyes dinámicas que rigen el movimiento: Principio de inercia; Principio de acción y reacción; y Principio fundamental de la dinámica, f = m * a
, y unas leyes dinámicas que rigen el movimiento: Principio de inercia; Principio de acción y reacción; y Principio fundamental de la dinámica, f = m * a - ↑ La Lógica de Aristóteles se mantuvo prácticamente como tal a lo largo de los siglos. Kant, a finales del siglo XVIII, opinaba que la Lógica aristotélica no había sufrido modificaciones sustanciales durante tanto tiempo por tratarse de una ciencia formal, a priori y analítica, y consideraba que había dado de sí todo lo que podía ofrecer
- ↑ La deducción suele definirse como una inferencia en la que a partir de verdades universales se concluye verdades particulares. Este criterio no se acomoda bien a la lógica actual, pues se prefiere la idea de inferencia como transformación conforme las reglas establecidas; en cualquier caso dichas reglas, que necesariamente se basan en tautologías, pueden considerarse como principios universales o generales, sobre los cuales se construye una deducción; por ello la distinción no deja de ser una matización técnica de poca importancia.
- ↑ La habilidad peculiar del Sr.Holmes
- ↑ Desgraciadamente la representación gráfica de los símbolos no está normalizada, lo que lleva a veces a ciertas dificultades de interpretación.
- ↑ ..."La aritmética no es, como tampoco, la geometría, una promoción natural de una razón inmutable. La Aritmética no está fundada en la razón. Es la doctrina de la razón la que está fundada en la aritmética elemental. Antes de saber contar apenas sabíamos qué era la razón. En general, el espíritu debe plegarse a las condiciones del saber”. Bachelard. Filosofía del No
- ↑ La grafía es normalmente aceptada como numeración arábiga, introducida en occidente en sustitución de la antigua numeración romana no posicional, que dificultaba enormemente los cálculos
- ↑ Por lo que el 0 a la izquierda no significa nada.
Bibliografía
- MITCHELL, D. (1968). INTRODUCCIÓN A LA LÓGICA. BARCELONA: EDITORIAL LABOR.
- DEAÑO, ALFREDO (1974). INTRODUCCIÓN A LA LÓGICA FORMAL. MADRID: ALIANZA EDITORIAL. ISBN 84-206-2064-5.
- QUINE, W.V. (1981). FILOSOFÍA DE LA LÓGICA. MADRID: ALIANZA EDITORIAL. ISBN 84-206-2043-2.
- COPI, IRVING M. (1982). LÓGICA SIMBÓLICA. MEXICO 22 D.F: EDITORIAL CONTINENTAL S.A. DE C.V.. ISBN 968-26-0134-7.
- Trueta i Raspall, J. et alii. (1977). Historia de la Ciencia. I. BARCELONA.ED.PLANETA. 84-320-0841-9.
- BERGADÁ, D. (1979). La matemática renacentista. Historia de la Ciencia. BARCELONA.ED.PLANETA. 84-320-0842-7.
- PERELLÓ I VALLS, C. (1979). El cálculo en los siglos XVII y XVIII. Historia de la Ciencia. BARCELONA.ED.PLANETA. 84-320-0842-7.
- HONDERICH, T. (Editor) (2001). Enciclopedia Oxford de Filosofía. Trd. Carmen García Trevijano. Madrid. Editorial Tecnos. 84-309-3699-2001.
- NAVARRO, C. Y NADAL, B. (1982). Aspectos de la Matemática en el siglo XX. Historia de la Ciencia. BARCELONA.ED.PLANETA. 81-320-0840-0.
- BUNGE, M. (1972). Teoría y realidad. Barcelona. Ariel.
- STEWART I. (1977). Conceptos de matemática moderna. Madrid. Alianza Universidad. 84-206-2187-0.
- BLACKBURN, S. (2001). Enciclopedia Oxford de Filosofía. Madrid. Editorial Tecnos. 84-309-3699-2001.
- Tablas de Aritmética. Ed.EDIVAS S.L. Ref. 25. Zamudio. España.
Enlaces externos
 .
.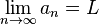
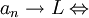
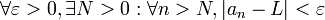
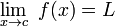
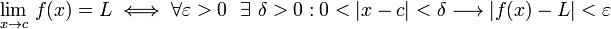
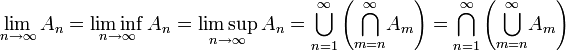
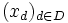 una red en X. Se dice que
una red en X. Se dice que 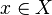 es un punto límite de la red
es un punto límite de la red 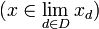 si la red está eventualmente en cada entorno de x, es decir, si cualquiera que sea el entorno V de x (esto es, cualquiera que sea el conjunto V de forma que exista un abierto G tal que
si la red está eventualmente en cada entorno de x, es decir, si cualquiera que sea el entorno V de x (esto es, cualquiera que sea el conjunto V de forma que exista un abierto G tal que 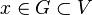 ) existe un
) existe un 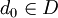 de tal forma que para cada
de tal forma que para cada 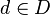 con
con 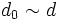 se cumple que
se cumple que 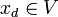 .
.
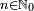 converge al valor 0, como se puede ver en la ilustración.
converge al valor 0, como se puede ver en la ilustración.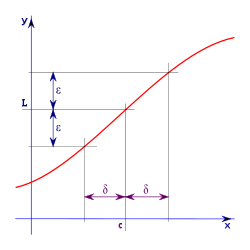
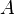 de
de 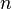 elementos, el número de permutaciones diferentes posibles es igual a la
elementos, el número de permutaciones diferentes posibles es igual a la 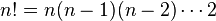 .
.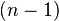 formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos
formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos 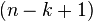 posibles elementos para escoger, lo que nos lleva a que tenemos
posibles elementos para escoger, lo que nos lleva a que tenemos 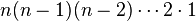 formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.
formas de ordenar el conjunto, justamente lo que enunciamos anteriormente. 
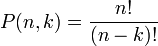 formas de construir un conjunto ordenado
formas de construir un conjunto ordenado 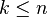 .
.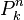 o
o ![left[{natop k}right]](https://petalofucsia.blogia.com/upload/externo-f0e7cec9be951a0596774e8298c3d5db.png) (en algunas partes del mundo se le conoce como
(en algunas partes del mundo se le conoce como 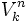 ).
).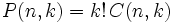
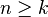 y cualquier conjunto finito con cardinal
y cualquier conjunto finito con cardinal 
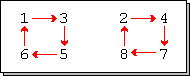
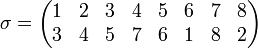
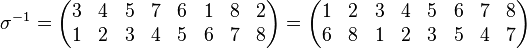
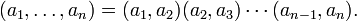
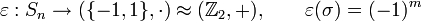
 es el
es el  tales que:
tales que: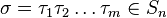
 , consideramos el conjunto
, consideramos el conjunto 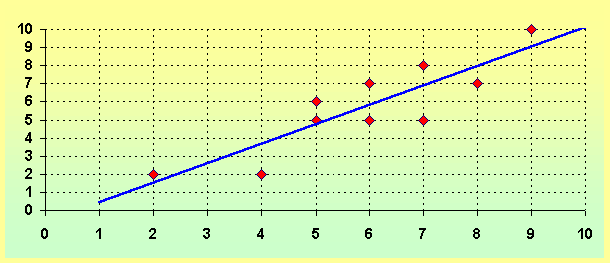
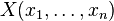 e
e 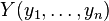 pueden estar consideradas como vectores en un espacio a n dimensiones. Reemplacemoslos por vectores centrados:
pueden estar consideradas como vectores en un espacio a n dimensiones. Reemplacemoslos por vectores centrados: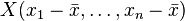 e
e 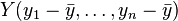 .
.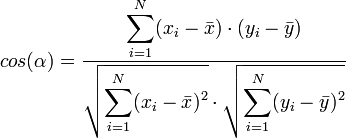




 B; A
B; A 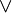 B; A
B; A 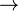 B; A
B; A 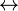 B, también lo son.
B, también lo son.![left [ left ( p land q right ) lor r right ]rightarrow t lor s](https://petalofucsia.blogia.com/upload/externo-cd43ae6ff74778d241c947e695d41d7c.png)
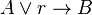
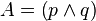 ; y donde
; y donde 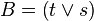
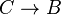
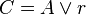
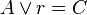
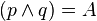 ; y donde
; y donde 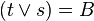
![[A land B land C....land N]rightarrow Y](https://petalofucsia.blogia.com/upload/externo-c736b8c23ddc520a6b1f4252e48d8428.png)
 Todos los posibles perros;
Todos los posibles perros;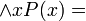 Para todo
Para todo 

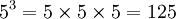
![sqrt[n]{x}](https://petalofucsia.blogia.com/upload/externo-3f61efd698b7851c132bb6cec4fe04ee.png) donde
donde 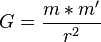 , y unas leyes dinámicas que rigen el movimiento: Principio de inercia; Principio de acción y reacción; y Principio fundamental de la dinámica,
, y unas leyes dinámicas que rigen el movimiento: Principio de inercia; Principio de acción y reacción; y Principio fundamental de la dinámica, 
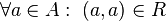
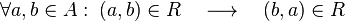

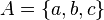

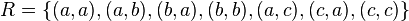
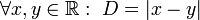
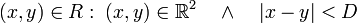 El par ordenado (x, y) cumple la relación de proximidad si x, y son números reales y la distancia entre x é y es menor que D.
El par ordenado (x, y) cumple la relación de proximidad si x, y son números reales y la distancia entre x é y es menor que D.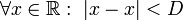 Para todo x número real, la distancia con si mismo es menor que D.
Para todo x número real, la distancia con si mismo es menor que D.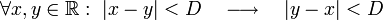 Si para todo x, y números reales, la distancia entre x é y es menor que D, entonces la distancia entre y y x también es menor que D.
Si para todo x, y números reales, la distancia entre x é y es menor que D, entonces la distancia entre y y x también es menor que D.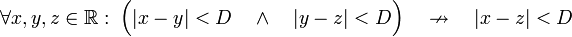 Si para todo x, y, z números reales, se cumple que la distancia entre x é y es menor que D, y la distancia entre y y z es menor que D, no implica necesariamente que la distancia entre x y z sea menor que D.
Si para todo x, y, z números reales, se cumple que la distancia entre x é y es menor que D, y la distancia entre y y z es menor que D, no implica necesariamente que la distancia entre x y z sea menor que D.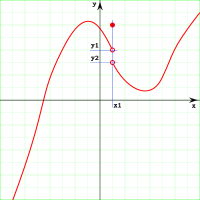
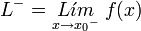
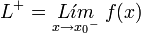
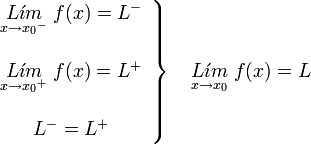
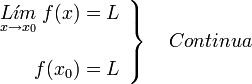

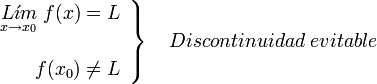
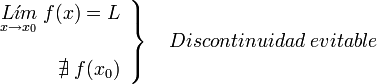

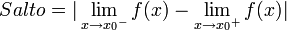
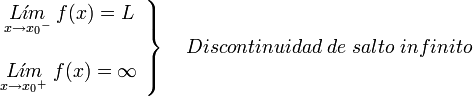
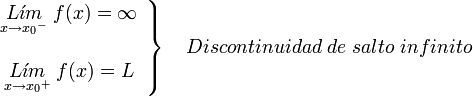
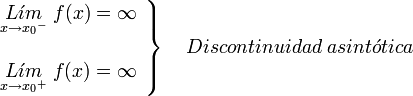
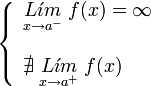
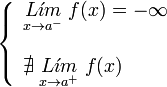
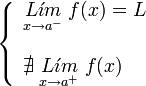
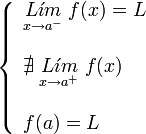
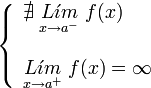
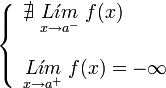
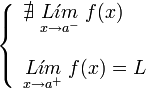
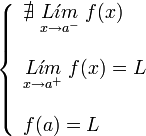
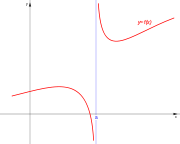
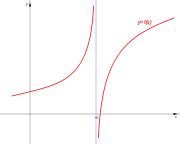
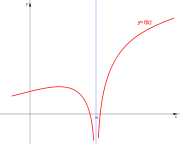
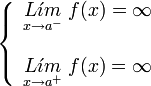
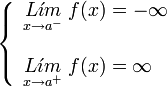
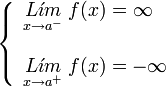
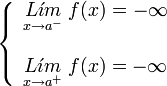
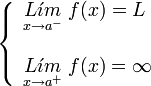
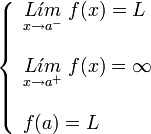
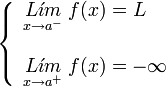
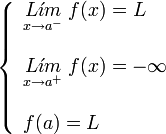
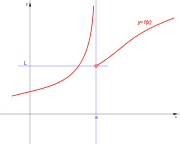
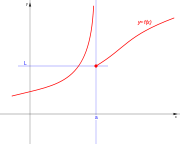
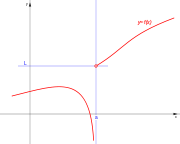
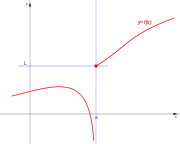
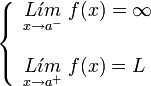
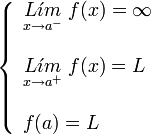
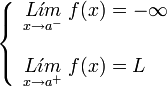
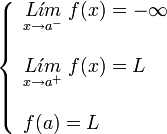
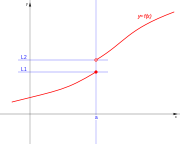
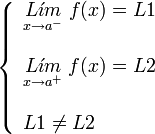
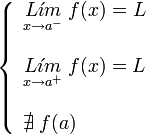
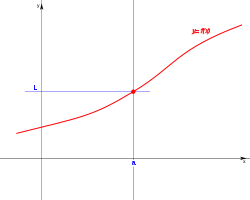
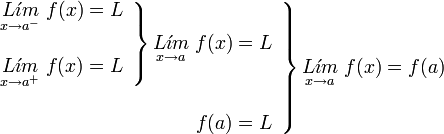
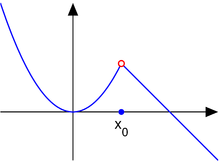
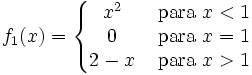
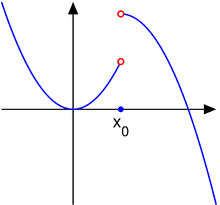
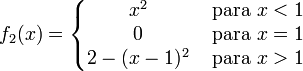
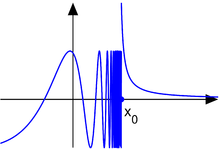
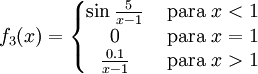
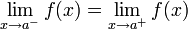
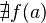
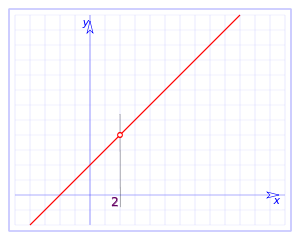
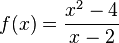
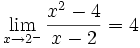
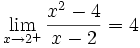
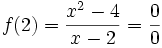
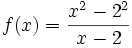
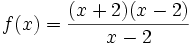
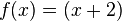
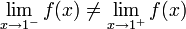
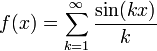
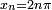 con
con  .
.
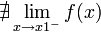 o
o 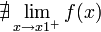
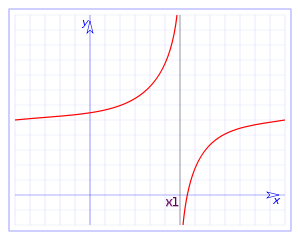
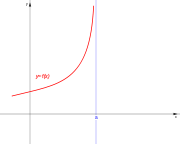
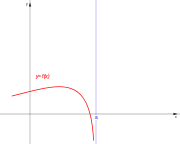
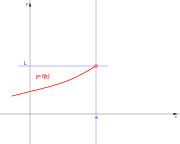
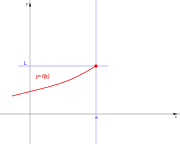
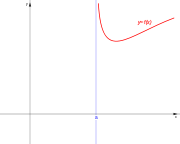
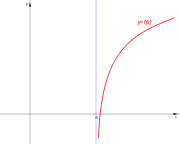
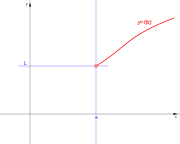
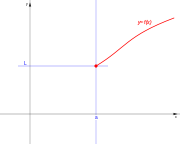
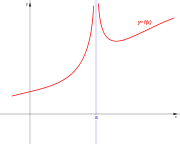
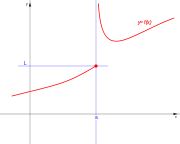
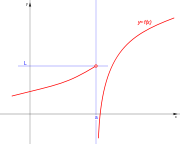
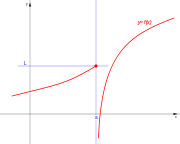
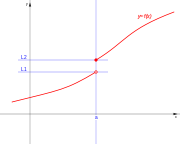
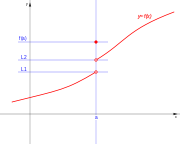
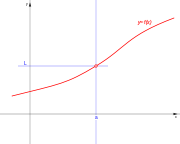
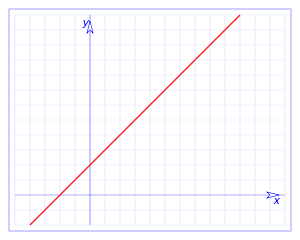
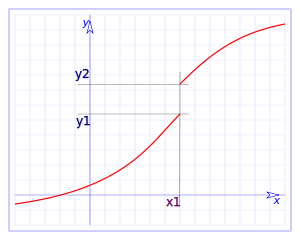
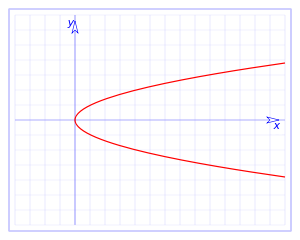
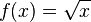 . Ésta tiene una discontinuidad de segunda especie en 0 pues no existe el límite:
. Ésta tiene una discontinuidad de segunda especie en 0 pues no existe el límite: