MATEMÁTICAS4: DISCONTINUIDAD. Las funciones continuas son de suma importancia en matemática y en distintas aplicaciones. Sin embargo, no todas las funciones son continuas. Puede ocurrir que una función no sea continua en todo su dominio de definición. Si una función no es continua en un punto, se dice que la función tiene una discontinuidad en ese punto y que la función es discontinua. En este artículo se describe la clasificación de discontinuidades para el caso más simple de funciones de una sola variable real.
Clasificación de discontinuidades
Las funciones continuas son de suma importancia en matemática y en distintas aplicaciones. Sin embargo, no todas las funciones son continuas. Puede ocurrir que una función no sea continua en todo su dominio de definición. Si una función no es continua en un punto, se dice que la función tiene una discontinuidad en ese punto y que la función es discontinua. En este artículo se describe la clasificación de discontinuidades para el caso más simple de funciones de una sola variable real.
Contenido |
[editar] Conceptos previos
Considérese una función f(x), de variable real x, definida para todo valor de x excepto posiblemente para un cierto valor x0. Es decir, f(x) está definida para x < x0 y para x > x0. Definamos también:
El límite por izquierda en x0, es decir, el límite al aproximarse al valor x = x0 mediante valores menores a x0, como:
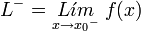
El límite por derecha en x0, es decir, el límite al aproximarse al valor x = x0 mediante valores mayores a x0, como:
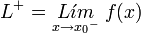
Si estos dos límites en el entorno del punto x0 existen y son iguales se dice que la función tiene limite en este punto.
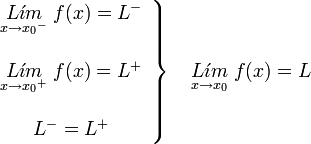
Si una función tiene limite en un punto y su valor coincide con el valor de la función en ese punto, entonces la función es continua en ese punto:
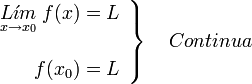
en cualquier otro caso es discontinua en ese punto.
[editar] Tipos de discontinuidades
La discontinuidad de una función puede ser clasificada en:

[editar] Discontinuidad evitable
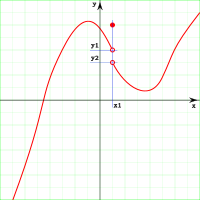
Si una función tiene limite en un punto, pero la función en ese punto tiene un valor distinto:
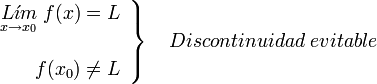
o no existe:
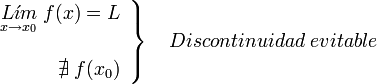
se dice que la discontinuidad es evitable, asignando a la función, en ese punto, el valor del limite:
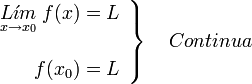
[editar] Discontinuidad esencial
Se dice que una función presenta una discontinuidad esencial cuando se produce algunas de las siguientes situaciones:
- Existen los límites laterales pero no coinciden.
- Alguno de los límites laterales o ambos son infinitos. Ver asíntota.
- No existe alguno de los límites laterales o ambos.
[editar] Discontinuidad de primera especie
En este tipo de discontinuidad existen tres tipos:
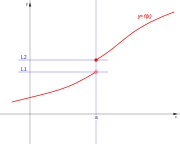
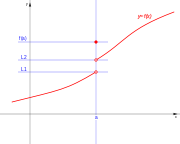
[editar] De salto finito
Existen el limite por la derecha y por la izquierda del punto, su valor es finito, pero no son iguales:

A este tipo de discontinuidad de primera especie se le llama salto finito, y el salto viene dado por:
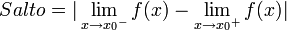
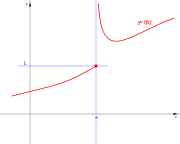
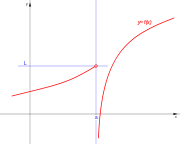
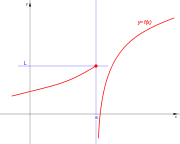
[editar] De salto infinito
Si uno de los limites laterales es infinito y el otro finito, tanto si el limite por la izquierda es finito y el de la derecha infinito:
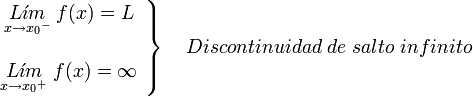
como en el caso de que el limite por la izquierda sea infinito y por la derecha finito:
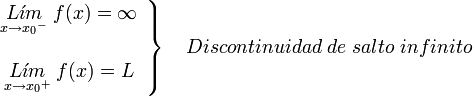
Se dice que la discontinuidad es de salto infinito.
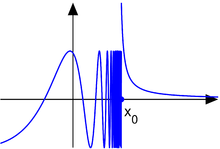
[editar] Discontinuidad asintótica
Si los dos limites laterales de la función en el punto x0 son infinitos:
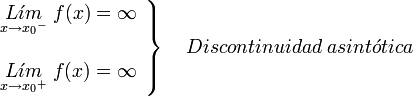
A este tipo de discontinuidad de primera especie se le llama discontinuidad asintótica, siendo x = a la asíntota.
[editar] Discontinuidad de segunda especie
Si la función no existe en uno de los lados del punto, o no existen alguno, o ambos, de los limites laterales de la función en ese punto, se dice que la función presenta una discontinuidad de segunda especie en ese punto.
[editar] Galería de discontinuidades
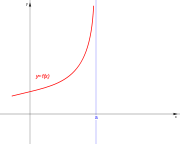 |  |  |  |
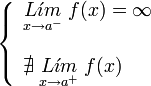 | 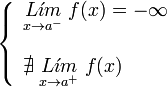 | 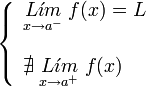 | 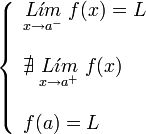 |
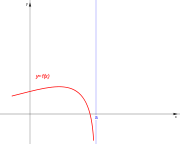
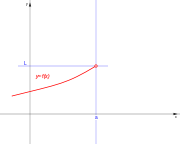
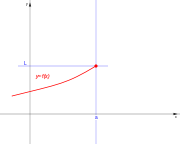
| De segunda especie. | De segunda especie. | De segunda especie. | De segunda especie. |
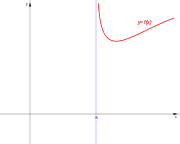 | 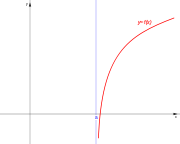 | 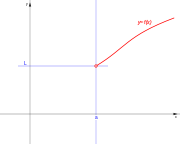 | 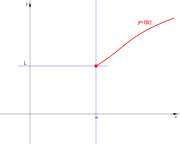 |
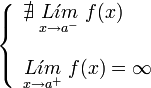 | 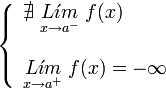 | 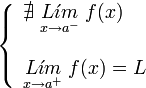 | 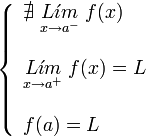 |
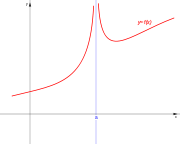
| De segunda especie. | De segunda especie. | De segunda especie. | De segunda especie. |
 |  |  |  |
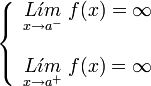 | 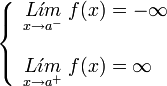 | 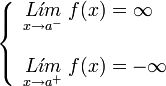 | 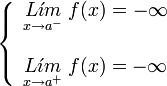 |
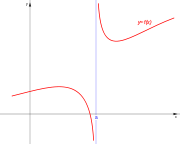
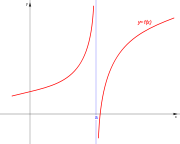
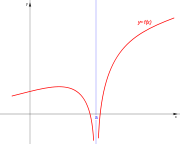
| Asintótica. | Asintótica. | Asintótica. | Asintótica. |
 |  |  |  |
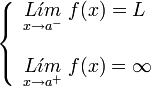 | 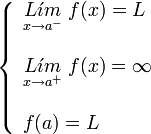 | 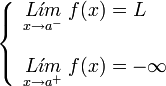 | 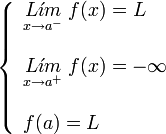 |
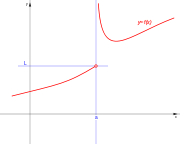
| De salto infinito. | De salto infinito. | De salto infinito. | De salto infinito. |
 |  |  |  |
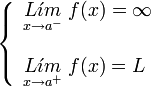 | 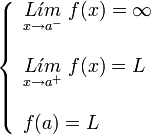 | 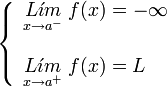 | 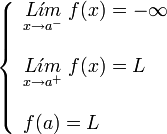 |
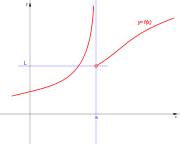
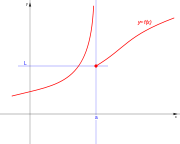
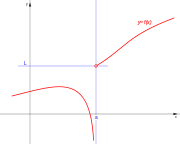
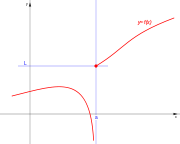
| De salto infinito. | De salto infinito. | De salto infinito. | De salto infinito. |
 |  |  |  |
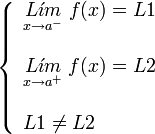 | 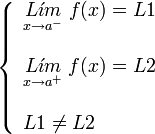 | 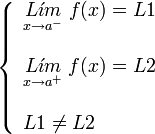 | 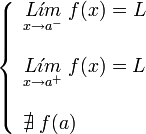 |
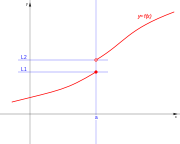
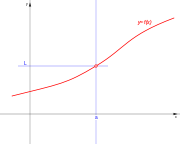
| De salto finito. | De salto finito. | De salto finito. | Evitable |
[editar] Caso de continuidad
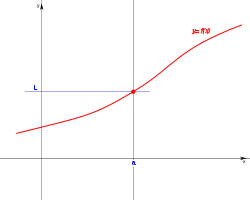
Una función y= f(x) es continua en un punto a, si los limites por la derecha y la izquierda son iguales, y coinciden con el valor de la función en ese punto.
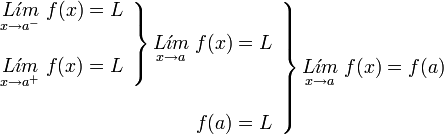
[editar] Ejemplos
- 1. Sea la función
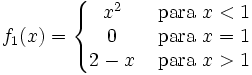
El punto x0 = 1 es una discontinuidad evitable. Esta función puede hacerse contínua simplemente redefiniendo la función en este punto para que valga f1(x0) = 1.
- 2. Sea la función
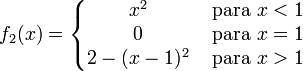
El punto x0 = 1 es una discontinuidad por salto.
- 3. Sea la función
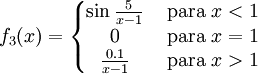
El punto x0 = 1 es una discontinuidad esencial, para lo cual hubiese bastado que uno de los dos límites laterales no exista o sea infinito (en este caso se cumple para ambos límites laterales: para el límite por izquierda y para el límite por derecha).
- 4. Funciones que no son continuas en ninguna parte
Existen funciones que no son continuas en ningún punto. La más conocida es la función característica de Q, es decir la función que toma como valor 1 cuando x pertenece al conjunto de los racionales, y 0 si no.
Obviamente, no se puede dibujar su curva, que está constituida por una infinidad de puntos en la recta y= 0, y una infinidad (menor) de puntos en la recta y= 1.
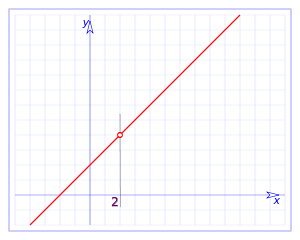
- 5. Discontinuidad evitable.
Una función presenta un punto de Discontinuidad evitable si en ese punto se cumple que:
Pueden ser transformadas en otra función continua, dándole a f(a) el valor adecuado que la hace continua. Si modificamos una función obtenemos otra función, no la misma, por ello se dice que son evitables.
ejemplo:La función:
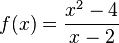
Presenta los siguientes limites por la izquierda y por la derecha:
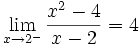
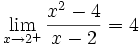
pero la función para x= 2 no esta definida:
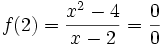
en este un caso de discontinuidad evitable y además de un modo sencillo:
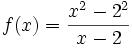
lo que es lo mismo:
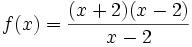
simplificando:
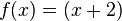
esta función es continua para todo x de valor real y es equivalente a la primera función, excepto en que la primera es discontinua para x= 2.
- 6. Discontinuidad de primera especie
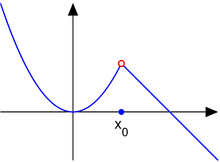
Una función presenta una discontinuidad de primera especie en un punto x1, si en este punto se cumple que:
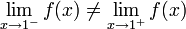
se produce un salto en los extremos.
Un ejemplo de función con discontinuidad de este estilo es por ejemplo:
Que es continua (y diferenciable) en todos los puntos, excepto en los puntos 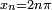 con
con 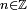 .
.
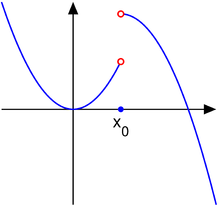
- 7. Discontinuidad de segunda especie
Son las que tienen puntos para los que existe solo uno de los limites laterales o ninguno.
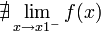 o
o 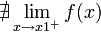
Por ejemplo la función 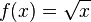 . Ésta tiene una discontinuidad de segunda especie en 0 pues no existe el límite:
. Ésta tiene una discontinuidad de segunda especie en 0 pues no existe el límite:
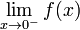
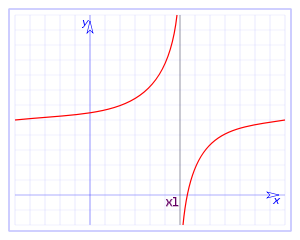
- 8. Discontinuidad asintótica
La discontinuidad viene marcada por una asíntota vertical. Se cumple lo siguiente:
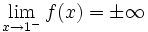
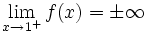
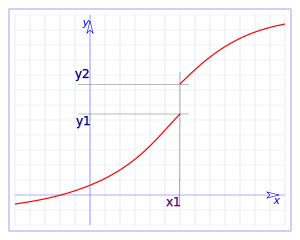
En la gráfica podemos ver la función:
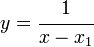
Donde x1 es un valor conocido, que presenta una asíntota vertical para x = x1
[editar] Véase también
- Función continua
- Gráfica de una función
- Representación gráfica de una función
- Lista de funciones matemáticas
- Derivación (matemática)
- Continuo
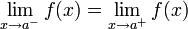
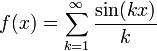
0 comentarios