MATEMÁTICAS4: ¿ES LO MISMO EL LÍMITE QUE EL TÉRMINO O EL FÍN?. En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
Límite matemático
| Uno o varios wikipedistas están trabajando actualmente en extender este artículo o sección. Es posible que a causa de ello haya lagunas de contenido o deficiencias de formato. Si quieres puedes ayudar y editar, pero por favor antes de realizar correcciones mayores contáctalos en sus páginas de discusión, o en la página de discusión del artículo para poder coordinar la redacción. |
En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.
Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(an) = a o se representa mediante la flecha (→) como en an → a.
Contenido[ocultar] |
[editar] Límite de una sucesión
La definición de límite matemático para el caso de una sucesión nos indica intuitivamente que los términos de la sucesión se aproximan arbitrariamente a un único número o punto L, si existe, para valores grandes de n. Esta definición es muy parecida a la definición del límite de una función cuando x tiende a 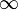 .
.
Formalmente, se dice que la sucesión an tiende hasta su límite L, o que converge o es convergente (a L), y se denota como:
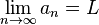
si y sólo si para todo valor real ε>0 se puede encontrar un número natural N tal que todos los términos de la sucesión, a partir de un cierto valor natural n mayor que N converjan a L cuando n crezca sin cota.
Escrito en un lenguaje formal, y de manera compacta:
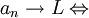
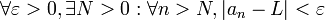
Este límite, si existe, se puede demostrar que es único. Si los términos de la sucesión no convergen a ningún punto específico, entonces se dice que la sucesión es divergente.
[editar] Límite de una función
En análisis real para funciones de una variable, se puede hacer una definición de límite similar a la de límite de una sucesión, en la cual, los valores que toma la función dentro de un intervalo se van aproximando a un punto fijado c, independientemente de que éste pertenezca al dominio de la función. Esto se puede generalizar aún más a funciones de varias variables o funciones en distintos espacios métricos.
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:
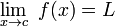
si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
Para un mayor rigor matemático se utiliza la definición épsilon-delta de límite, que es más escricta y convierte al límite en una gran herramienta del análisis real. Su definición es la siguiente:
"El límite de f de x cuando x tiende a c es igual a L si y sólo si para todo número real ε mayor que cero existe un número real δ mayor que cero tal que si la distancia entre x y c es menor que δ, entonces la distancia entre la imagen de x y L es menor que ε unidades".
Esta definición, se puede escribir utilizando términos lógico-matemáticos y de manera compacta:
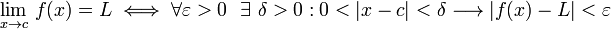
[editar] Límite de una sucesión de conjuntos
En teoría de conjuntos también se utiliza el concepto de límite, que se puede calcular sobre una sucesión de conjuntos. Para ello, los conjuntos deben de cumplir una serie de condiciones, como puede ser la monotonía (creciente o decreciente). De manera más general, y utilizando la definición de límite superior y límite inferior para una sucesión de conjuntos cualquiera An, se dice que el límite de esta sucesión existe si el límite superior y límite inferior existen y son iguales,
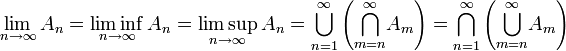
Estos conceptos son muy útiles en disciplinas de las matemáticas como la teoría de la medida, especialmente en espacios de probabilidad.
[editar] Límites en redes topológicas
Todas las nociones anteriores de límite pueden ser unificadas y generalizadas a espacios topológicos arbitrarios mediante la introducción de redes topológicas y la definición de sus límites.
Sea (X,T) un espacio topológico y 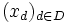 una red en X. Se dice que
una red en X. Se dice que 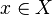 es un punto límite de la red
es un punto límite de la red 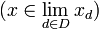 si la red está eventualmente en cada entorno de x, es decir, si cualquiera que sea el entorno V de x (esto es, cualquiera que sea el conjunto V de forma que exista un abierto G tal que
si la red está eventualmente en cada entorno de x, es decir, si cualquiera que sea el entorno V de x (esto es, cualquiera que sea el conjunto V de forma que exista un abierto G tal que 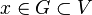 ) existe un
) existe un 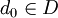 de tal forma que para cada
de tal forma que para cada 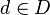 con
con 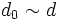 se cumple que
se cumple que 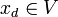 .
.
[editar] Límites en teoría de categorías
En teoría de categorías, una rama de la matemática, se define el concepto abstracto de límite, el cual usa propiedades esenciales de construcciones universales tales como productos y límites inversos.
[editar] Véase también
- Continuidad (matemáticas)
- Límite de una sucesión
- Límite de una función
- Límite de una red topológica
- Límite superior y límite inferior
- Límite (teoría de categorías)
[editar] Referencias
[editar] Enlaces externos
- Weisstein, Eric W., «Límite matemático» (en inglés), MathWorld, Wolfram Research, http://mathworld.wolfram.com/Limit.html, consultado el 29 de mayo de 2010.
- Mathwords: Limit
- Límites de funciones. Introducción
- Introducción al Cálculo de Límites (vídeo)

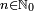 converge al valor 0, como se puede ver en la ilustración.
converge al valor 0, como se puede ver en la ilustración.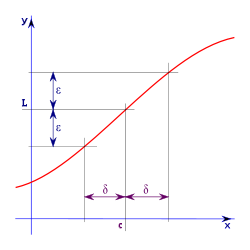
2 comentarios
petalofucsia -
petalofucsia -
Estamos tratando las Profecías pero no se nos permite poner nada aquí por temor a que no se haga, pero sí se me permitió adelantarles esta Gran Profecía.