MATEMÁTICAS3: FRACTALES. BENOIT MANDELBROT. Benoît Mandelbrot (Varsovia, Polonia, 20 de noviembre de 1924 Cambridge, Estados Unidos, 14 de octubre de 2010[1] ) fue un matemático conocido por sus trabajos sobre los fractales. Es considerado el principal responsable del auge de este dominio de las matemáticas desde el inicio de los años setenta, y del interés creciente del público. En efecto, supo utilizar la herramienta que se estaba popularizando en ésta época - el ordenador - para trazar los más conocidos ejemplos de geometría fractal: el conjunto de Mandelbrot por supuesto, así como los conjuntos de Julia descubiertos por Gaston Julia quien inventó las matemáticas de los fractales, desarrollados luego por Mandelbrot.
Benoît Mandelbrot
| Benoît Mandelbrot | |
|---|---|
 Mandelbrot en 2007 | |
| Nacimiento | 20 de noviembre de 1924 |
| Fallecimiento | 14 de octubre de 2010 (85 años) |
| Nacionalidad | francesa - estadounidense |
| Campo | Matemáticas |
| Instituciones | Universidad de Yale IBM Pacific Northwest National Laboratory |
| Alma máter | École Polytechnique California Institute of Technology Universidad de París |
| Estudiantes destacados | F. Kenton Musgrave Eugene F. Fama |
| Conocido por | Conjunto de Mandelbrot |
| Premios destacados | Premio Wolf (1993) Premio Japón (2003) |


Benoît Mandelbrot (Varsovia, Polonia, 20 de noviembre de 1924 – Cambridge, Estados Unidos, 14 de octubre de 2010[1] ) fue un matemático conocido por sus trabajos sobre los fractales. Es considerado el principal responsable del auge de este dominio de las matemáticas desde el inicio de los años setenta, y del interés creciente del público. En efecto, supo utilizar la herramienta que se estaba popularizando en ésta época - el ordenador - para trazar los más conocidos ejemplos de geometría fractal: el conjunto de Mandelbrot por supuesto, así como los conjuntos de Julia descubiertos por Gaston Julia quien inventó las matemáticas de los fractales, desarrollados luego por Mandelbrot.
Contenido[ocultar] |
[editar] Biografía
Nació el 20 de noviembre de 1924 en Varsovia, Polonia dentro de una familia judía culta de origen lituano. Fue introducido al mundo de las matemáticas desde pequeño gracias a sus dos tíos. Cuando su familia emigra a Francia en 1936 su tío Szolem Mandelbrot, profesor de matemáticas en el Collège de France y sucesor de Hadamardost en este puesto, toma responsabilidad de su educación. Después de realizar sus estudios en la Universidad de Lyon ingresó a la École polytechnique, a temprana edad, en 1944 bajo la dirección de Paul Lévy quien también lo influyó fuertemente. Se doctoró en matemáticas por la Universidad de París en el año 1952. Posteriormente se fue al MIT y Luego al Instituto de Estudios Avanzados de Pricenton, donde fue el último estudiante de postdoctorado a cargo de John von Neumann. Después de diversas estancias en Ginebra y París acabó trabajando en IBM Research.
En 1967 publicó en Science «¿Cuánto mide la costa de Gran Bretaña?», donde se exponen sus ideas tempranas sobre los fractales.
Fue profesor de economía en la Universidad Harvard, ingeniería en Yale, fisiología en el Colegio Albert Einstein de Medicina, y matemáticas en París y Ginebra. Desde 1958 trabajó en IBM en el Centro de Investigaciones Thomas B. Watson en Nueva York.
[editar] Logros científicos
Principal creador de la Geometría Fractal, al referirse al impacto de esta disciplina en la concepción e interpretación de los objetos que se encuentran en la naturaleza. En 1982 publicó su libro Fractal Geometry of Nature en el que explicaba sus investigaciones en este campo. La geometría fractal se distingue por una aproximación más abstracta a la dimensión de la que caracteriza a la geometría convencional.
El profesor Mandelbrot se interesó por cuestiones que nunca antes habían preocupado a los científicos, como los patrones por los que se rigen la rugosidad o las grietas y fracturas en la naturaleza.
Mandelbrot sostuvo que los fractales, en muchos aspectos, son más naturales, y por tanto mejor comprendidos intuitivamente por el hombre, que los objetos basados en la geometría euclidiana, que han sido suavizados artificialmente.
[editar] Controversias
Mandelbrot indicó la sobrevaloración de las matemáticas basadas en análisis algebraico desde el siglo XIX y otorgó igual importancia a la geometría y al análisis matemático visual, análisis para el que él estaba especialmente dotado, sobre la que mantuvo se han hecho logros igual o más importantes como los de los antiguos griegos o Da Vinci. Esta visión poco ortodoxa, le costó duras críticas por parte de los mátemáticos más 'puros', especialmente al inicio de su carrera.
[editar] Honores y premios
En 1985 recibió el premio "Barnard Medal for Meritorious Service to Science". En los años siguientes recibió la "Franklin Medal". En 1987 fue galardonado con el premio "Alexander von Humboldt"; también recibió la "Medalla Steindal" en 1988 y muchos otros premios, incluyendo la "Medalla Nevada" en 1991.
[editar] Conjunto de Mandelbrot
El conjunto de Mandelbrot es un conjunto matemático de puntos en el plano complejo, cuyo borde forma un fractal. Este conjunto se define así, en el plano complejo:
Sea c un número complejo cualquiera. A partir de c, se construye una sucesión por inducción:
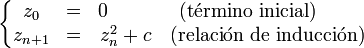
Si esta sucesión queda acotada, entonces se dice que c pertenece al conjunto de Mandelbrot, y si no, queda excluido del mismo.
[editar] Referencias
- ↑ Jascha Hoffman (16 de octubre de 2010). «Benoit Mandelbrot, Mathematician, Dies at 85» (en inglés). The New York Times. Consultado el 16 de octubre de 2010. «Benoit B. Mandelbrot, a maverick mathematician who developed an innovative theory of roughness and applied it to physics, biology, finance and many other fields, died on Thursday in Cambridge, Mass. He was 85.».
[editar] Véase también
- Fractal
- Conjunto de Mandelbrot
- ¿Cuánto mide la costa de Gran Bretaña?
- La geometría fractal de la naturaleza
[editar] Enlaces externos
 Wikimedia Commons alberga contenido multimedia sobre Benoît Mandelbrot.Commons
Wikimedia Commons alberga contenido multimedia sobre Benoît Mandelbrot.Commons Wikiquote alberga frases célebres de o sobre Benoît Mandelbrot. Wikiquote
Wikiquote alberga frases célebres de o sobre Benoît Mandelbrot. Wikiquote- Entrevista de Eduard Punset a Benoît Mandelbrot.
- Página web B.Mandelbrot en Yale. (en inglés)
- Ted talk: "Benoit Mandelbrot: Fractals and the art of roughness"
- Museo de Arte Fractal Argentina
- Fractales en la naturaleza aérea de Doñana. Armonía fractal de Doñana y las marismas
- Obituario de Benoît Mandelbrot (The Economist)















0 comentarios