MATEMÁTICAS4: CLARO QUE ALGO TENÍA QUE HABER AL COMIENZO, SINO NUNCA SE HUBIESE ORIGINADO NADA, ESE ALGO, ¿ERA NUESTRA ESENCIA DIVINA Y ESPIRITUAL? IMAGINESE QUE NO HUBIESE NADA, UN CERO, ¿YA NO SE PODRÍA HABLAR DE MATEMÁTICA, NO LE PARECE? ¿SIEMPRE QUE HAY UNA CANTIDAD EN EL ORÍGEN, SE PUEDE HABLAR DE MATEMÁTICA? Y ¿ES LA MATEMÁTICA PERFECTA? CLARO QUE AL COMIENZO DEBÍA DE HABER ALGO, UNA CANTIDAD, ALGO QUE DIÓ ORÍGEN A TODO, SINO NO SERÍA POSIBLE HABLAR DE MATEMÁTICA.

31 de diciembre de 2010 - 12:25 - Matemáticas4

Raíz de una función

De Wikipedia, la enciclopedia libre

Si busca la raíz enésima de un número, vea Función raíz.

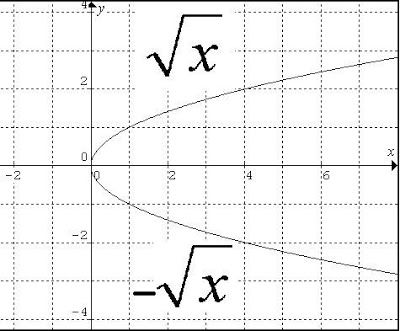
¿ALGUNA VEZ LA RAÍZ DE UNA FUNCIÓN O DE UN NÚMERO ES O?

En matemática, se conoce como raíz (o cero) de una función (definida sobre un cierto cuerpo algebraico) f (x) a todo elemento x perteneciente al dominio de dicha función tal que se cumpla:

$f(x) = 0 ,$ .

Por ejemplo, dada la función:

$f(x) = x^2 - 6x + 8 ,$

Planteando y resolviendo la ecuación:

$0 = x^2 - 6x + 8 ,$

Se tine que 2 y 4 son raíces (ver ecuación de segundo grado) ya que f(2) = 0 y f(4) = 0.

Contenido

[ocultar]

[editar] Buscando raíces

Dado el caso de que tanto el dominio como la imagen de la función sean los números reales (denominadas funciones reales) entonces los puntos en los que el gráfico corta al eje de las abscisas es una interpretación gráfica de las raíces de dicha función.
El teorema fundamental del álgebra determina que todo polinomio en una variable compleja y de grado n tiene n raíces (contando sus multiplicidades). Aun así, Las raíces de los polinomios reales no son necesariamente reales; algunas de ellas, o incluso todas, pueden ser complejas.
Una función trascendente como por ejemplo 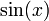$sin(x),$ posee una infinidad de raíces, concretamente cualquier 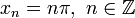$x_n = npi, ninmathbb{Z}$ es raíz de esa función. En cambio la función $e z$ no se anula nunca sobre los números complejos.
El número de raíces de una función holomorfa o una función analítica es un conjunto numerable sin puntos de acumulación.
Uno de los problemas no resueltos más interesantes de la matemática moderna es encontrar las raíces de la función zeta de Riemann.

[editar] Raíces simples y múltiples

Dada una función f que tiene una raíz r entonces se puede escribir dicha función como:

$f(x) = (x-r)f_1(x),$

Entonces se dice que:

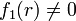
La raíz es simple si $f_1(r)ne 0,$
La raíz es multiple si 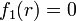$f_1(r)= 0,$ , en este último caso la raíz se dice de orden n, siendo $n > 1$ , cuando se puede escribir:

$f(x) = (x-r)^nf_n(x),quad mbox{con} f_n(r)ne 0,$

[editar] Métodos para buscar raíces

[editar] Teoremas sobre raíces

Dada una función real o compleja el número de raíces es siempre numerable, puediendo ser cero, número finito o un número infinito numerable.

El teorema fundamental del álgebra afirma que cualquier polinomio de grado n sobre 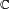$scriptstyle mathbb{C}$ tiene a lo sumo n raíces diferentes, y si se cuenta la multiplicidad de cada raíz entonces puede afirmarse que existen exactamente n raíces.
La función 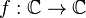$f:mathbb{C} to mathbb{C}$ dada por $f (z) = e z$ no tienen ninguna raíz ya que no se anula nunca.
Las funciones reales $sin(x)$ y $cos(x)$ tienen un número infinito numerable de raíces.

Obtenido de "http://es.wikipedia.org/wiki/Ra%C3%ADz_de_una_funci%C3%B3n"

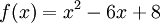
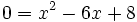
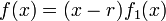
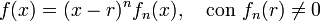
2 comentarios

petalofucsia - 31 de diciembre de 2010 - 12:32

Piense, ¿si todo variase, incluso nuestro orígen, no se hablaría de "Caos"? ¿habría estabilidad?, ¿nos haríamos todos distintos?

¿no son necesarias unas constantes que garanticen esta armonía entre todos?

Imaginese que la esencia no fuese invariable y todos comenzasemos a cambiar, no se podría hablar de armonía, ¿sería caótico?

petalofucsia - 31 de diciembre de 2010 - 12:29

Pero, ¿cómo se explica que en el orígen deba de haber algo? ¿se tratará de la parte invariable de todo?

¿que opina?

Diccionario de la lengua española © 2005 Espasa-Calpe:
invariable
1.adj. Que no cambia o no puede cambiar:
la preposición y el adverbio son partes invariables de la oración.

Preguntas en los foros con la(s) palabra(s) 'invariable' en el título:

Ningún título tiene la(s) palabra(s) 'invariable'.Pregunta tú mismo.
Visita el foro.
Discussions in the 'Solo español' forum

'invariable' también aparece en estas entradas
adverbio - afro - antiarrugas - antibalas - anticarro - anticaspa - antidopaje - antidoping - antidroga - antiestrés - antigás - antiniebla - antirradar - antirrobo - antitanque - añil - bíter - conjunción - fijo - inmóvil - invariabilidad - multirriesgo - multiuso - porno - preposición - que - regla - retro - todoterreno

Diccionario de sinónimos y antónimos © 2005 Espasa-Calpe:
invariable
inalterable, inconmovible, inmutable, estable, eterno, fijo, perenne, permanente, constante
◦Antónimos: mudable, fluctuante

'invariable' también aparece en estas entradas
estable - estancado - estático - estereotipado - fijo - inalterado - irreversible - monótono - sedentario - sistemático

invariable.

1. adj. Que no varía o no puede variar.

Real Academia Española © Todos los derechos reservados

------

¿Podría ser también una constante, la parte invariable?