MATEMÁTICAS2: MEDIA ARMÓNICA. La media armónica , denominada H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores.
Media armónica
De Wikipedia, la enciclopedia libre

La media armónica , denominada H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores
Así, dados los números a1,a2, ... , an, la media armónica será igual a:
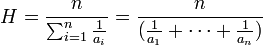
La media armónica resulta poco influida por la existencia de determinados valores mucho más grandes que el conjunto de los otros, siendo en cambio sensible a valores mucho más pequeños que el conjunto.
La media armónica no está definida en el caso de la existencia en el conjunto de valores nulos.
Contenido[ocultar] |
[editar] Propiedades
- La inversa de la media armónica es la media aritmética de los inversos de los valores de la variable.
- Siempre se puede pasar de una media armónica a una media aritmética transformando adecuadamente los datos.
[editar] Ventajas
- Considera todos los valores de la distribución y
- en ciertos casos, es más representativa que la media aritmética.
[editar] Desventajas
- La influencia de los valores pequeños y
- El hecho que no se puede determinar en las distribuciones con algunos valores iguales a cero; por eso no es aconsejable su empleo en distribuciones donde existan valores muy pequeños.
Se suele utilizar para promediar velocidades, tiempos, rendimientos, etc.
[editar] Referencia
[editar] Bibliografía
- 'Introducción a la Estadística Económica y Empresarial. Teoría y Práctica.' de Fco. Javier Martín-Pliego López, Editorial Thomson, 2007 (Madrid).
- 'Manual de Estadística Empresarial con ejercicios resueltos' de Eva Ropero, María Eleftheriou, Luana Gava y Eva Romero. Editorial Delta Publicaciones. 2008 (Madrid).
0 comentarios