Blogia
petalofucsia

MATEMÁTICAS2: ESTUDIE ESTO: ¿QUÉ PASARÍA SI TODOS LOS NÚMEROS FUESEN SIMÉTRICOS UNOS DE OTROS? ¿SE DARÍA LA PERFECCIÓN? ¿CÓMO SE EXPLICA QUE AÚN NO HAYA PERFECCIÓN? ¿NACIMOS DESORDENADOS?. TRATE DE ORDENAR CON SIMETRÍA TODOS LOS NÚMEROS, ¿QUÉ RESULTADO DA?

- Matemáticas2

Grupo simétrico

De Wikipedia, la enciclopedia libre
Grafo de Cayley de un grupo simétrico de orden 4 (S4) representado como el grupo de rotaciones de un dado convencional.

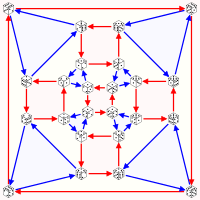
En matemáticas, el grupo simétrico sobre un conjunto X, denotado por SX es el grupo formado por las funciones biyectivas (permutaciones) de X en sí mismo.

Los subgrupos de SX se denominan grupos de permutaciones. El Teorema de Cayley afirma que todo grupo G es isomorfo a un grupo de permutaciones (ie: un subgrupo del simétrico).

De especial relevancia es el grupo simétrico sobre el conjunto finito X = {1,...,n}, denotado por Sn. El grupo Sn tiene orden n! y no es abeliano para n>2.

 

Contenido

[ocultar]

[editar] Composición de permutaciones

Hay diversas formas de representar una permutación. Podemos escribir una permutación σ en forma de matriz, situando en primera fila los elementos del dominio 1, 2, 3..., y en la segunda las imágenes correspondientes σ(1), σ(2), σ(3),....

Dada dos permutaciones, su composición se realiza siguiendo las reglas usuales de composición de funciones:

Si  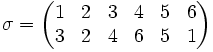 sigma = begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 3 & 2 & 4 & 6 & 5 & 1 end{pmatrix}  y  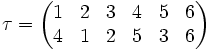 tau = begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 4 & 1 & 2 & 5 & 3 & 6 end{pmatrix}

su composición es: 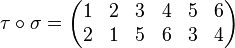tau circ sigma = begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 2 & 1 & 5 & 6 & 3 & 4 end{pmatrix}

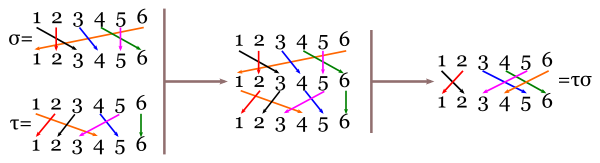
El cálculo de la composición puede seguirse de un modo visual, recordando que al componer funciones se opera de derecha a izquierda:

Composicion de permutaciones.svg

[editar] Una presentación del grupo

[editar] Generadores

Recordemos que una trasposición es una permutación que intercambia dos elementos y fija los restantes. Toda permutación se descompone como producto de trasposiciones. De este modo, el conjunto de las trasposiciones forma un sistema generador de Sn. Pero es posible reducir aún más este sistema restringiéndonos a las trasposiciones de la forma τi = (i,i + 1). En efecto, para i<j podemos descomponer cualquier trasposición en la forma:

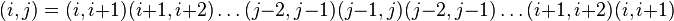
(i,j)=(i,i+1)(i+1,i+2)dots (j-2,j-1)(j-1,j)(j-2,j-1)dots (i+1,i+2)(i,i+1)

[editar] Relaciones elementales

Estos generadores permiten definir una presentación del grupo simétrico, junto con las relaciones:

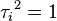  • {tau_i}^2 = 1, ,
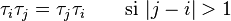  • tau_itau_j = tau_jtau_i qquad mbox{si } |j-i| > 1,,
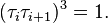  • {(tau_itau_{i+1}})^3=1.,.

[editar] Otros generadores

Es posible igualmente usar como sistema de generadores:

  • Las trasposiciones de la forma (1 i), con i>1.
  • El conjunto formado por solo dos generadores:la trasposición σ=(1 2) y el ciclo c=(1 2 ... n).

[editar] Clases de conjugación

Recordemos que toda permutación puede ser descrita como producto de ciclos disjuntos, y esta descomposición es única salvo el orden de los factores. Las clases de conjugación de Sn se corresponden con la estructura de dicha descomposición en ciclos: dos permutaciones son conjugadas en Sn si y sólo si se obtienen como composición del mismo número de ciclos disjuntos de las mismas longitudes. Por ejemplo, en S5, (1 2 3)(4 5) y (1 4 3)(2 5) son conjugados; pero (1 2 3)(4 5) y (1 2)(4 5) no.

El grupo S3, formado por las 6 permutaciones de tres elementos tiene tres clases de conjugación, listadas con sus números de elementos:

  • La identidad (abc → abc) (1)
  • Las permutaciones que intercambian dos elementos (abc → acb, abc → bac, abc → cba) (3)
  • Las permutaciones ciclicas de los 3 elementos (abc → bca, abc → cab) (2)

El grupo S4, consistente en las 24 permutaciones de 4 elementos tiene 5 clases de conjugación:

  • La identidad (1)
  • Las permutaciones que intercambian dos elementos (6)
  • Las permutaciones que intercambian cíclicamente tres elementos (8)
  • Las permutaciones cíclicas de los cuatro elementos (6)
  • Las permutaciones que intercambian dos elementos entre sí, y también los dos restantes (3)

En general, cada clase de conjugación en Sn se corresponderá con una partición entera de n y podrá ser representada gráficamente por un diagrama de Young. Así, por ejemplo, las cinco particiones de 4 se corresponderían con las cinco clases de conjugación listadas anteriormente:

  1. 1 + 1 + 1 + 1
  2. 2 + 1 + 1
  3. 3 + 1
  4. 4
  5. 2 + 2

[editar] Representaciones del grupo

Si asociamos a cada permutación su matriz permutación obtenemos una representación que en general no es irreducible.[1]

[editar] Representaciones irreducibles

[editar] Referencias

  1. ↑ Sternberg, S. Group Theory and Physics. Cambridge University Press, 1994. ISBN 0 521 24870 1
Obtenido de "http://es.wikipedia.org/wiki/Grupo_sim%C3%A9trico"

0 comentarios