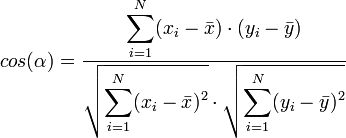MATEMÁTICAS: ALGEBRA. El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades (en el caso del álgebra elemental). Es una de las principales ramas de la matemática, junto a la geometría, el análisis matemático, la combinatoria y la teoría de números.
Álgebra
El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades (en el caso del álgebra elemental). Es una de las principales ramas de la matemática, junto a la geometría, el análisis matemático, la combinatoria y la teoría de números.
La palabra «álgebra» es de origen árabe, deriva del tratado escrito por el matemático persa Muhammad ibn Musa al-Jwarizmi, titulado Kitab al-yabr wa-l-muqabala (en árabe كتاب الجبر والمقابلة) (que significa "Compendio de cálculo por el método de completado y balanceado"), el cual proporcionaba operaciones simbólicas para la solución sistemática de ecuaciones lineales y cuadráticas. Etimológicamente, la palabra «álgebra» جبر (yabr) , proviene del árabe y significa "reducción".
Contenido[ocultar] |
[editar] Álgebra elemental
Álgebra elemental es la forma más básica del álgebra. A diferencia de la aritmética, en donde solo se usan los números y sus operaciones aritméticas (como +, −, ×, ÷), en álgebra los números son representados por símbolos (usualmente a, b, c, x, y, z). Esto es útil porque:
- Permite la formulación general de leyes de aritmética (como a + b = b + a), y esto es el primer paso para una exploración sistemática de las propiedades de los números reales.
- Permite referirse a números "desconocidos", formular ecuaciones y el estudio de cómo resolverlas.
- Permite la formulación de relaciones funcionales.
[editar] Historia
Si bien la palabra "álgebra" viene de la palabra árabe (al-Jabr, الجبر), sus orígenes se remontan a los antiguos babilonios, que habían desarrollado un avanzado sistema aritmético con el que fueron capaces de hacer cálculos en una forma algebraica. Con el uso de este sistema fueron capaces de aplicar las fórmulas y soluciones para calcular valores desconocidos. Este tipo de problemas suelen resolverse hoy mediante ecuaciones lineales, ecuaciones de segundo grado y ecuaciones indefinidas. Por el contrario, la mayoría de los egipcios de esta época, y la mayoría de la India, griegos y matemáticos chinos en el primer milenio antes de Cristo, normalmente resolvían tales ecuaciones por métodos geométricos, tales como los descritos en la matemática Rhind Papyrus, Sulba Sutras, Elementos de Euclides, y los Nueve Capítulos sobre el Arte de las Matemáticas. El trabajo geométrico de los griegos, centrado en las formas, dio el marco para la generalización de las fórmulas más allá de la solución de los problemas particulares de carácter más general, sino en los sistemas de exponer y resolver ecuaciones.
Las mentes griegas matemáticas de Alejandría y Diofanto siguieron las tradiciones de Egipto y Babilonia, pero el Diophantus del libro Arithmetica está en un nivel mucho más alto. Más tarde, los matemáticos árabes y musulmanes desarrollaron métodos algebraicos a un grado mucho mayor de sofisticación. Aunque los babilonios y Diophantus utilizaron sobre todo los métodos especiales ad hoc para resolver ecuaciones, Al-Khowarizmi fue el primero en resolver ecuaciones usando métodos generales. Él resolvió el indeterminado de ecuaciones lineales, ecuaciones cuadráticas, ecuaciones indeterminadas de segundo orden y ecuaciones con múltiples variables.
La palabra "álgebra" es el nombre de la palabra árabe "Al-Jabr, الجبر" en el título del libro al-Kitab al-muḫtaṣar fi al-Gabr ḥisāb wa-l-muqābala, الكتاب المختصر في حساب الجبر والمقابلة, el sentido del Resumen del libro se refiere a la transposición y Cálculo de la Reducción de un libro escrito por el matemático persa islámico, Muhammad ibn Musa Al-Khwārizmī (considerado el "padre del álgebra"), en 820. La palabra Al-Jabr significa "reducción". El matemático helenístico Diophantus ha sido tradicionalmente conocido como el "padre del álgebra", pero en tiempos más recientes, hay mucho debate sobre si al-Khwarizmi, que fundó la disciplina de Al-Jabr, título que se merece su lugar. Los que apoyan Diophantus apuntan al hecho de que el álgebra que se encuentra en Al-Jabr es algo más elemental que el que se encuentra en el álgebra Arithmetica y que Arithmetica es sincopada mientras que Al-Jabr es totalmente retórica. Los que apoyan el punto de Al-Khwarizmi sobre el hecho de que presenta los métodos de "reducción" y "equilibrio" (la transposición de términos restará al otro lado de una ecuación, es decir, la cancelación de términos a ambos lados de la ecuación), al cual el término Al-Jabr se refería originalmente, y que dio una explicación exhaustiva de la solución de ecuaciones cuadráticas, apoyada por las pruebas geométricas, mientras que el tratamiento de álgebra como una disciplina independiente en su propio derecho. Su álgebra ya tampoco trataría "con una serie de los problemas por resolver", sino con una "exposición que empieza con lo primitivo en el que las combinaciones deben dar todos los posibles prototipos de ecuaciones, que en adelante explícitamente constituyen el verdadero objeto de estudio". También estudió una ecuación para su propio bien y "de forma genérica, en la medida que no sólo surgen en el curso de la solución de un problema, sino que específicamente en la llamada para definir una infinidad de problemas de clase".
El matemático persa Omar Khayyam desarrolló la geometría algebraica y encontró la solución geométrica de la ecuación cúbica. Otro matemático persa, Sharaf Al-Din al-Tusi, encontró la solución numérica y algebraica a diversos casos de ecuaciones cúbicas. Él también desarrolló el concepto de una función. Los matemáticos indios Mahavirá y Bhaskara II, el matemático persa Al-Karaji, y el matemático chino Zhu Shijie, resolvieron varios casos de cúbicos, quartic, quintic y ecuaciones polinómicas de orden superior mediante métodos numéricos.
Otro acontecimiento clave en el desarrollo del álgebra fue la solución algebraica de las ecuaciones cúbicas y quárticas, desarrollado a mediados del siglo XVI. La idea de un factor determinante fue desarrollada por el matemático japonés Kowa Seki en el siglo XVII, seguido por Gottfried Leibniz diez años más tarde, con el fin de resolver sistemas de ecuaciones lineales simultáneas utilizando matrices. Gabriel Cramer también hizo un trabajo sobre matrices y determinantes en el siglo XVIII. Resumen de álgebra se desarrolló en el siglo XIX, centrándose inicialmente en lo que ahora se llama la teoría de Galois, y en cuestiones de constructibilidad.
[editar] Estructura algebraica
En matemáticas, una estructura algebraica es un conjunto de elementos con unas propiedades operacionales determinadas; es decir, lo que define a la estructura del conjunto son las operaciones que se pueden realizar con los elementos de dicho conjunto y las propiedades matemáticas que dichas operaciones poseen. Un objeto matemático constituido por un conjunto no vacío y algunas leyes de composición interna definida en él es una estructura algebraica. Las estructuras algebraicas más importantes son:
| Estructura | Ley interna | Asociatividad | Neutro | Inverso | Conmutatividad |
|---|---|---|---|---|---|
| Magma | |||||
| Semigrupo | |||||
| Monoide | |||||
| Monoide abeliano | |||||
| Grupo | |||||
| Grupo abeliano |
| Estructura (A,+,·) | (A,+) | (A,·) |
|---|---|---|
| Semianillo | Monoide abeliano | Monoide |
| Anillo | Grupo abeliano | Semigrupo |
| Cuerpo | Grupo abeliano | Grupo abeliano |
[editar] Signos y símbolos
En el álgebra se utilizan signos y símbolos -en general utilizados en la teoría de conjuntos- que constituyen ecuaciones, matrices, series, etc. Sus letras son llamadas variables, ya que se usa esa misma letra en otros problemas y su valor va variando.
Aquí algunos ejemplos:
| Signos y Símbolos | |
| Expresión | Uso |
|---|---|
| + | Además de expresar adición, también es usada para expresar operaciones binarias |
| c ó k | Expresan Términos constantes |
| Primeras letras del abecedario a, b, c,... | Se utilizan para expresar cantidades conocidas |
| Últimas letras del abecedario ...,x, y, z | Se utilizan para expresar incógnitas |
| n | Expresa cualquier número (1,2,3,4,...,n) |
Exponentes y subíndices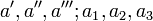 | Expresar cantidades de la misma especie, de diferente magnitud. |
[editar] Véase también
 Portal:Álgebra. Contenido relacionado con Álgebra.
Portal:Álgebra. Contenido relacionado con Álgebra.- Álgebra elemental
- Teorema fundamental del álgebra
[editar] Enlaces externos
 Wikimedia Commons alberga contenido multimedia sobre Álgebra. Commons
Wikimedia Commons alberga contenido multimedia sobre Álgebra. Commons Wikiquote alberga frases célebres de o sobre Álgebra. Wikiquote
Wikiquote alberga frases célebres de o sobre Álgebra. Wikiquote Wikcionario tiene definiciones para álgebra.Wikcionario
Wikcionario tiene definiciones para álgebra.Wikcionario Wikiversidad alberga proyectos de aprendizaje sobre Álgebra.Wikiversidad
Wikiversidad alberga proyectos de aprendizaje sobre Álgebra.Wikiversidad- Videos de Algebra




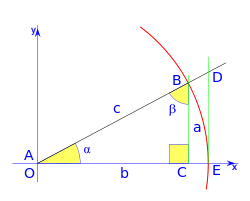

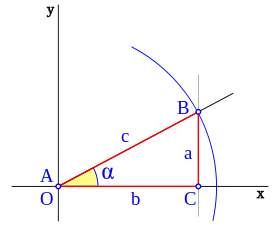
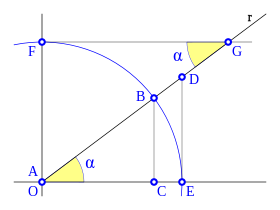
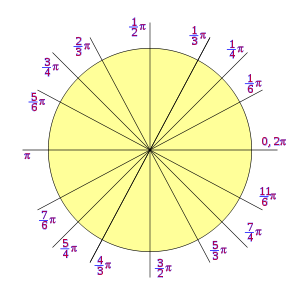
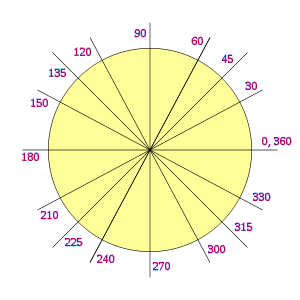
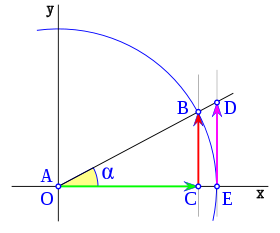
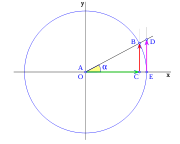
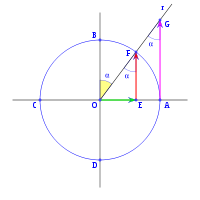
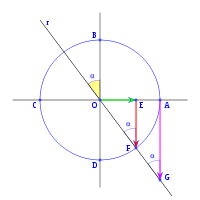
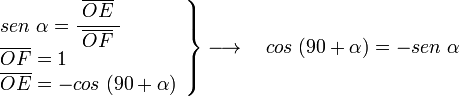
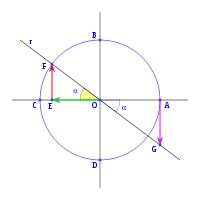
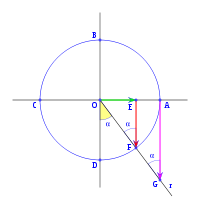
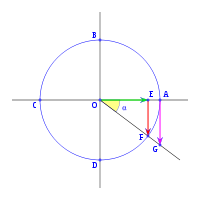
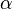 , correspondiente al vértice A, situado en el centro de la circunferencia.
, correspondiente al vértice A, situado en el centro de la circunferencia.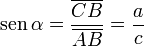
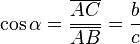
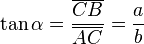
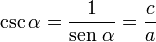
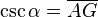
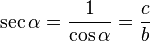
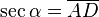
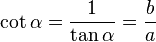
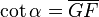
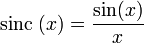
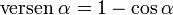
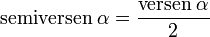
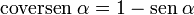
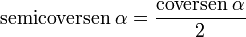
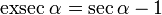
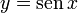
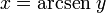
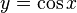
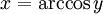
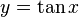
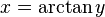

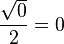
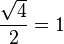
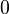
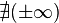
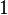

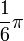
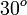
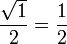
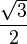
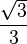
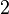
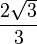
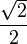
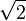
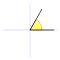
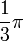
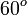
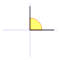
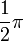
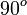
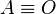
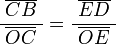
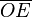 y
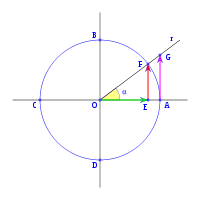
y 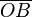 son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas: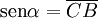
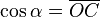
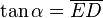
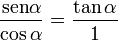
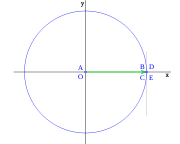
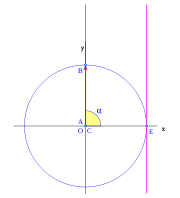
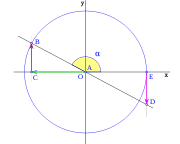
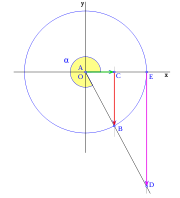
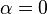 , tenemos que B, D, y C coinciden en E, por tanto:
, tenemos que B, D, y C coinciden en E, por tanto: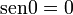
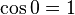
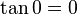
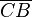 y
y 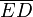 aumentarán progresivamente, mientras que
aumentarán progresivamente, mientras que 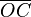 disminuirá.
disminuirá.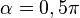
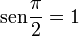
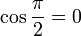
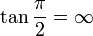
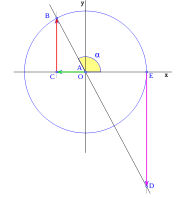
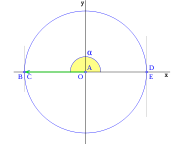
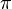

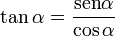
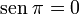
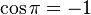
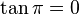
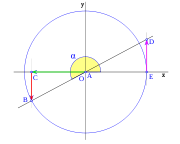
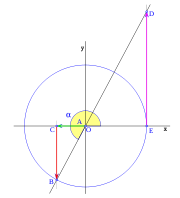
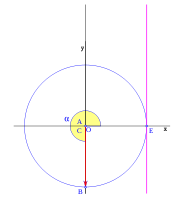
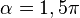
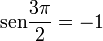
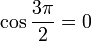
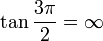
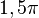
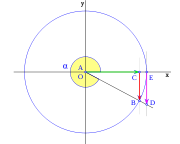
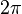
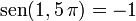
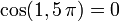

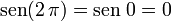
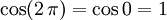
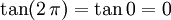
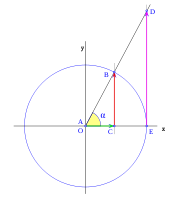
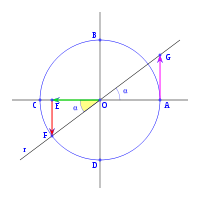
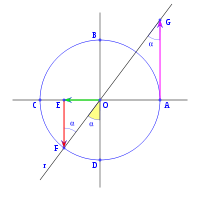
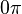 al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.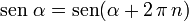
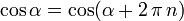
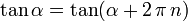

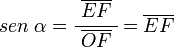
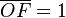
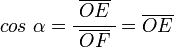
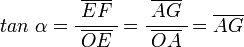
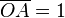
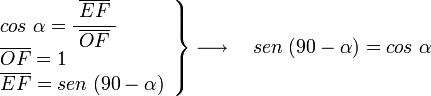
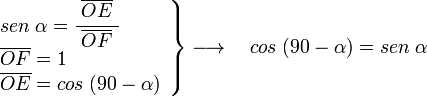
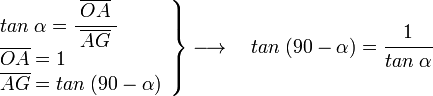
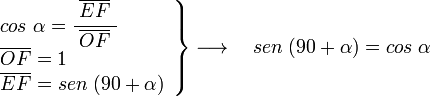
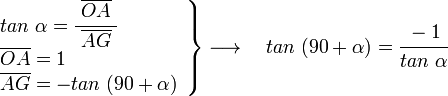
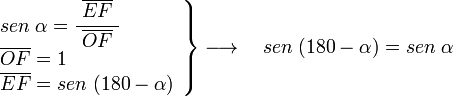

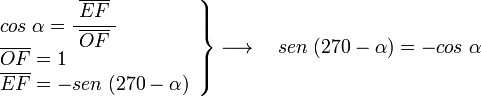
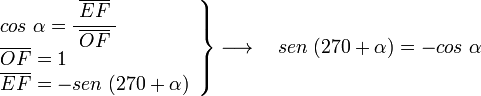
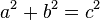
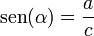
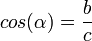
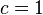

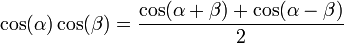
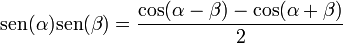
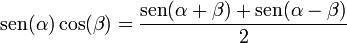
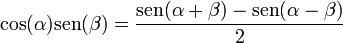
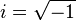 (también puede representarse como j).
(también puede representarse como j).

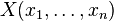 e
e 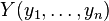 pueden estar consideradas como vectores en un espacio a n dimensiones. Reemplacemoslos por vectores centrados:
pueden estar consideradas como vectores en un espacio a n dimensiones. Reemplacemoslos por vectores centrados: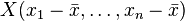 e
e 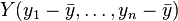 .
.