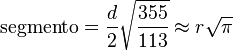De Wikipedia, la enciclopedia libre
π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
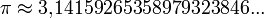
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Por ello, tal vez sea la constante que más pasiones desata entre los matemáticos profesionales y aficionados. La relación entre la circunferencia y su diámetro no es constante en geometrías no euclídeas.
[editar] El nombre π

Letra griega pi. Símbolo adoptado en
1706 por William Jones y popularizado por
Leonhard Euler.
La notación con la letra griega π proviene de la inicial de las palabras de origen griego "περιφέρεια" (periferia) y "περίμετρον" (perímetro) de un círculo,[1] notación que fue utilizada primero por William Oughtred (1574-1660), y propuesto su uso por el matemático galés William Jones[2] (1675-1749), aunque fue el matemático Leonhard Euler, con su obra «Introducción al cálculo infinitesimal» de 1748, quien la popularizó. Fue conocida anteriormente como constante de Ludolph (en honor al matemático Ludolph van Ceulen) o como constante de Arquímedes (que no se debe confundir con el número de Arquímedes).
[editar] Historia del cálculo del valor π
La búsqueda del mayor número de decimales del número π ha supuesto un esfuerzo constante de numerosos científicos a lo largo de la historia. Algunas aproximaciones históricas de π son las siguientes.
[editar] Antiguo Egipto
El valor aproximado de π en las antiguas culturas se remonta a la época del escriba egipcio Ahmes en el año 1800 a. C., descrito en el papiro Rhind,[3] donde se emplea un valor aproximado de π afirmando que: el área de un círculo es similar a la de un cuadrado, cuyo lado es igual al diámetro del círculo disminuido en 1/9, es decir, igual a 8/9 del diámetro. En notación moderna:
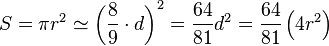
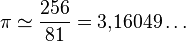
Entre los ocho documentos matemáticos hallados de la antigua cultura egipcia, en dos se habla de círculos. Uno es el papiro Rhind y el otro es el papiro de Moscú. Sólo en el primero se habla del valor aproximado del número π. El investigador Otto Neugebauer, en un anexo de su libro The Exact Sciences in Antiquity,[4] describe un método inspirado en los problemas del papiro de Ahmes para averiguar el valor de π, mediante la aproximación del área de un cuadrado de lado 8, a la de un círculo de diámetro 9.
[editar] Mesopotamia
Algunos matemáticos mesopotámicos empleaban, en el cálculo de segmentos, valores de π igual a 3, alcanzando en algunos casos valores más aproximados, como el de 3 + 1/8.
[editar] Referencias bíblicas
Una de las referencias indirectas más antiguas del valor aproximado de π se puede encontrar en un versículo de la Biblia:
«Hizo fundir asimismo un mar de diez
codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos.»
Una cita similar se puede encontrar en II Crónicas 4:2. En él aparece en una lista de requerimientos para la construcción del Gran Templo de Salomón, construido sobre el 950 a. C. Ambas citas dan 3 como valor de π lo que supone una notable pérdida de precisión respecto de las anteriores estimaciones egipcia y mesopotámica.
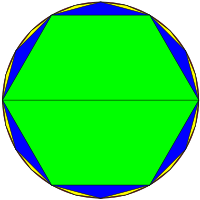
Método de
Arquímedes para encontrar dos valores que se aproximen al número
π, por exceso y defecto.
[editar] Antigüedad clásica
El matemático griego Arquímedes (siglo III a. C.) fue capaz de determinar el valor de π, entre el intervalo comprendido por 3 10/71, como valor mínimo, y 3 1/7, como valor máximo. Con esta aproximación de Arquímedes se obtiene un valor con un error que oscila entre 0,024% y 0,040% sobre el valor real. El método usado por Arquímedes[5] era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.
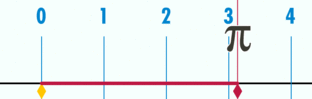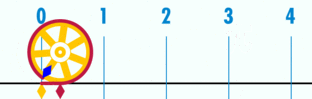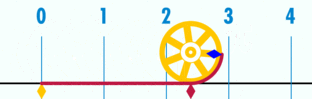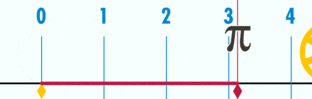
Alrededor del año 20 d. C., el arquitecto e ingeniero romano Vitruvio calcula π como el valor fraccionario 25/8 midiendo la distancia recorrida en una revolución por una rueda de diámetro conocido.
En el siglo II, Claudio Ptolomeo proporciona un valor fraccionario por aproximaciones:
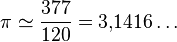
[editar] Matemática china
El cálculo de pi fue una atracción para los matemáticos expertos de todas las culturas. Hacia 120, el astrólogo chino Chang Hong (78-139) fue uno de los primeros en usar la aproximación 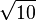 , que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo Wang Fang lo estimó en 142/45 (3,155555), aunque se desconoce el método empleado.[6] Pocos años después, hacia 263, el matemático Liu Hui fue el primero en sugerir[7] que 3,14 era una buena aproximación, usando un polígono de 96[8] o 192[6] lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3.072 lados.[8] [9]
, que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo Wang Fang lo estimó en 142/45 (3,155555), aunque se desconoce el método empleado.[6] Pocos años después, hacia 263, el matemático Liu Hui fue el primero en sugerir[7] que 3,14 era una buena aproximación, usando un polígono de 96[8] o 192[6] lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3.072 lados.[8] [9]
A finales del siglo V, el matemático y astrónomo chino Zu Chongzhi calculó el valor de π en 3,1415926 al que llamó «valor por defecto» y 3,1415927 «valor por exceso», y dio dos aproximaciones racionales de π: 22/7 y 355/113 muy conocidas ambas,[10] siendo la última aproximación tan buena y precisa que no fue igualada hasta más de nueve siglos después, en el siglo XV.[8]
[editar] Matemática india
Usando un polígono regular inscrito de 384 lados, a finales del siglo V el matemático indio Aryabhata estimó el valor en 3,1416. A mediados del siglo VII, estimando incorrecta la aproximación de Aryabhata, Brahmagupta calcula π como 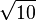 , cálculo mucho menos preciso que el de su predecesor. Hacia 1400 Madhava obtiene una aproximación exacta hasta 11 dígitos (3,14159265359), siendo el primero en emplear series para realizar la estimación.[6]
, cálculo mucho menos preciso que el de su predecesor. Hacia 1400 Madhava obtiene una aproximación exacta hasta 11 dígitos (3,14159265359), siendo el primero en emplear series para realizar la estimación.[6]
[editar] Matemática islámica
En el siglo IX Al-Jwarizmi en su "Álgebra" (Hisab al yabr ua al muqabala) hace notar que el hombre práctico usa 22/7 como valor de π, el geómetra usa 3, y el astrónomo 3,1416. En el siglo XV, el matemático persa Ghiyath al-Kashi fue capaz de calcular el valor aproximado de π con nueve dígitos, empleando una base numérica sexagesimal, lo que equivale a una aproximación de 16 dígitos decimales: 2π = 6,2831853071795865.
[editar] Renacimiento europeo
A partir del siglo XII, con el uso de cifras arábigas en los cálculos, se facilitó mucho la posibilidad de obtener mejores cálculos para π. El matemático Fibonacci, en su «Practica Geometriae», amplifica el método de Arquímedes, proporcionando un intervalo más estrecho. Algunos matemáticos del siglo XVII, como Viète, usaron polígonos de hasta 393.216 lados para aproximarse con buena precisión a 3,141592653. En 1593 el flamenco Adriaan van Roomen (Adrianus Romanus) obtiene una precisión de 16 dígitos decimales usando el método de Arquímedes.
[editar] Época moderna (pre-computacional)
En 1610 el matemático Ludolph van Ceulen calculó los 35 primeros decimales de π. Se dice que estaba tan orgulloso de esta hazaña que lo mandó grabar en su lápida. Los libros de matemática alemanes durante muchos años denominaron a π como número ludolfiano. En 1665 Isaac Newton desarrolla la serie[11]
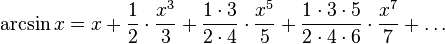
Con 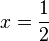 obtuvo una serie para
obtuvo una serie para 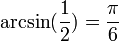 .
.
El matemático inglés John Wallis desarrolló en 1655 la conocida serie Producto de Wallis:
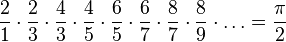
.
En 1699, a sugerencia de Edmond Halley, el matemático inglés Abraham Sharp (1651-1742) calculó pi con una precisión de 71 dígitos decimales usando la serie de Gregory:
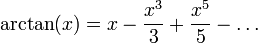
Con 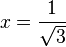 se obtiene una serie para
se obtiene una serie para 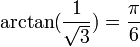 . Para alcanzar la precisión obtenida, debió usar alrededor de trescientos términos en la serie. En 1720 el francés Thomas de Lagny utilizó el mismo método para obtener una aproximación de 127 dígitos (solo los primeros 112 eran correctos).
. Para alcanzar la precisión obtenida, debió usar alrededor de trescientos términos en la serie. En 1720 el francés Thomas de Lagny utilizó el mismo método para obtener una aproximación de 127 dígitos (solo los primeros 112 eran correctos).
Leibniz calculó de una forma más complicada en 1682 la siguiente serie matemática que lleva su nombre:
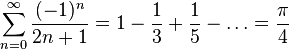
.
Fue en el año 1706 cuando el galés William Jones afirmó: «3,14159 andc. = π». Leonhard Euler adoptó el conocido símbolo en 1737, que se convirtió en la notación habitual hasta nuestros días.
El matemático japonés Takebe empezó a calcular el número π en el año 1722, con el mismo método expuesto por Arquímedes, y fue ampliando el número de lados para polígonos circunscritos e inscritos hasta llegar a 1.024 lados. Este ingente trabajo consiguió que se determinara π con 41 decimales.
En 1789 el matemático de origen esloveno Jurij Vega, mediante la fórmula de John Machin, descubierta en 1706, fue el primero en averiguar los primeros 140 decimales de π, de los cuales 126 eran correctos; este récord se mantuvo durante 52 años, hasta que en 1841 William Rutherford calculó 208 decimales, de los cuales 152 eran correctos.
El matemático aficionado de origen inglés William Shanks dedicó cerca de 20 años a calcular π y llegó a obtener 707 decimales en 1873. En el año 1944, D. F. Ferguson encontró un error en la posición decimal 528 de la serie de Shanks, a partir del cual todos los dígitos posteriores eran erróneos. En 1947, Ferguson recalculó π con 808 decimales con la ayuda de una calculadora mecánica.
Algunas aproximaciones históricas de valores de π, anteriores a la época computacional, se muestran en la siguiente tabla:
| Año | Matemático o documento | Cultura | Aproximación | Error
(en partes por millón) |
| ~1900 a. C. | Papiro de Ahmes | Egipcia | 28/34 ~ 3,1605 | 6016 ppm |
| ~1600 a. C. | Tablilla de Susa | Babilónica | 25/8 = 3,125 | 5282 ppm |
| ~600 a. C. | La Biblia (Reyes I, 7,23) | Judía | 3 | 45070 ppm |
| ~500 a. C. | Bandhayana | India | 3,09 | 16422 ppm |
| ~250 a. C. | Arquímedes de Siracusa | Griega | entre 3 10/71 y 3 1/7
empleó 211875/67441 ~ 3,14163 | <402 ppm
13,45 ppm |
| ~150 | Claudio Ptolomeo | Greco-egipcia | 377/120 = 3,141666... | 23,56 ppm |
| 263 | Liu Hui | China | 3,14159 | 0,84 ppm |
| 263 | Wang Fan | China | 157/50 = 3,14 | 507 ppm |
| ~300 | Chang Hong | China | 101/2 ~ 3,1623 | 6584 ppm |
| ~500 | Zu Chongzhi | China | entre 3,1415926 y 3,1415929
empleó 355/113 ~ 3,1415929 | <0,078 ppm
0,085 ppm |
| ~500 | Aryabhata | India | 3,1416 | 2,34 ppm |
| ~600 | Brahmagupta | India | 101/2 ~ 3,1623 | 6584 ppm |
| ~800 | Al-Juarismi | Persa | 3,1416 | 2,34 ppm |
| 1220 | Fibonacci | Italiana | 3,141818 | 72,73 ppm |
| 1400 | Madhava | India | 3,14159265359 | 0,085 ppm |
| 1424 | Al-Kashi | Persa | 2π = 6,2831853071795865 | 0,1 ppm |
[editar] Época moderna (computacional)
Desde el diseño de la primera computadora se empezaron a desarrollar programas para el cálculo del número π con la mayor cantidad de cifras posible. De esta forma, en 1949 un ENIAC fue capaz de romper todos los récords, obteniendo 2.037 cifras decimales en 70 horas. Poco a poco fueron surgiendo ordenadores que batían récords y, de esta forma, pocos años después (1954) un NORAC llegó a 3.092 cifras. Durante casi toda la década de los años 1960 los IBM fueron batiendo récords, hasta que un IBM 7030 pudo llegar en 1966 a 250.000 cifras decimales (en 8 h y 23 min). Durante esta época se probaban las nuevas computadoras con algoritmos para la generación de series de números procedentes de π.
En la década de 2000, los ordenadores son capaces de obtener números que poseen una inmensa cantidad de decimales. En 2009 se hallaron más de dos billones y medio de decimales de pi mediante el uso de una supercomputadora T2K Tsukuba System, compuesta por 640 computadoras de alto rendimiento, que juntas consiguen velocidades de procesamiento de 95 teraflops. Lo obtuvieron en 73 horas y 36 minutos.
| Año | Descubridor | Ordenador utilizado | Número de cifras decimales |
| 1949 | G.W. Reitwiesner y otros[12] | ENIAC | 2.037 |
| 1954 | | NORAC | 3.092 |
| 1959 | Guilloud | IBM 704 | 16.167 |
| 1967 | | CDC 6600 | 500.000 |
| 1973 | Guillord y Bouyer[12] | CDC 7600 | 1.001.250 |
| 1981 | Miyoshi y Kanada[12] | FACOM M-200 | 2.000.036 |
| 1982 | Guilloud | | 2.000.050 |
| 1986 | Bailey | CRAY-2 | 29.360.111 |
| 1986 | Kanada y Tamura[12] | HITAC S-810/20 | 67.108.839 |
| 1987 | Kanada, Tamura, Kobo y otros | NEC SX-2 | 134.217.700 |
| 1988 | Kanada y Tamura | Hitachi S-820 | 201.326.000 |
| 1989 | Hermanos Chudnovsky | CRAY-2 y IBM-3090/VF | 480.000.000 |
| 1989 | Hermanos Chudnovsky | IBM 3090 | 1.011.196.691 |
| 1991 | Hermanos Chudnovsky | | 2.260.000.000 |
| 1994 | Hermanos Chudnovsky | | 4.044.000.000 |
| 1995 | Kanada y Takahashi | HITAC S-3800/480 | 6.442.450.000 |
| 1997 | Kanada y Takahashi | Hitachi SR2201 | 51.539.600.000 |
| 1999 | Kanada y Takahashi | Hitachi SR8000 | 68.719.470.000 |
| 1999 | Kanada y Takahashi | Hitachi SR8000 | 206.158.430.000 |
| 2002 | Kanada y otros[12] [3] | Hitachi SR8000/MP | 1.241.100.000.000 |
| 2004 | | Hitachi | 1.351.100.000.000 |
| 2009 | Daisuke Takahashi[13] | T2K Tsukuba System | 2.576.980.370.000 |
| 2009 | Fabrice Bellard[14] | Core i7 CPU, 2.93 GHz; RAM: 6GiB | 2.699.999.990.000 |
En la época computacional del cálculo de π las cifras se han disparado, no sólo debido a la potencia de cálculo que estas máquinas son capaces de generar, sino también por el prestigio que conlleva para el constructor de la máquina cuando su marca aparece en la lista de los récords.
[editar] Características matemáticas

Se muestra la relación entre un cuadrado de lado
r y un círculo de radio
r. El área del
círculo es
πr2.
[editar] Definiciones
Euclides fue el primero en demostrar que la relación entre una circunferencia y su diámetro es una cantidad constante.[15] No obstante, existen diversas definiciones del número π, pero las más común es:
Por tanto, también π es:
También es posible definir analíticamente π; dos definiciones son posibles:
- Le ecuación sobre los números complejos eix + 1 = 0 admite una infinidad de soluciones reales positivas, la más pequeña de las cuales es precisamente π.
- La ecuación diferencial S''(x) + S(x) = 0 con las condiciones de contorno S(0) = 0,S'(0) = 1 para la que existe solución única, garantizada por el teorema de Picard-Lindelöf, es un función analítica cuya raíz positiva más pequeña es precisamente π.
[editar] Número irracional y trascendente
Se trata de un número irracional, lo que significa que no puede expresarse como fracción de dos números enteros, como demostró Johann Heinrich Lambert en 1761 (o 1767). También es un número trascendente, es decir, que no es la raíz de ningún polinomio de coeficientes enteros. En el siglo XIX el matemático alemán Ferdinand Lindemann demostró este hecho, cerrando con ello definitivamente la permanente y ardua investigación acerca del problema de la cuadratura del círculo indicando que no tiene solución.
También se sabe que π tampoco es un número de Liouville (Mahler,[16] 1953), es decir, no sólo es trascendental sino que no puede ser aproximado por una secuencia de racionales "rápidamente convergente" (Stoneham 1970[cita requerida]).
[editar] Las primeras cincuenta cifras decimales
A pesar de tratarse de un número irracional continúa siendo averiguada la máxima cantidad posible de decimales. Los cincuenta primeros son:
π ≈ 3,1415926535 8979323846 2643383279 5028841971 6939937510
Para ver secuencias mayores de este número consúltese las referencias, así como Las primeras diez mil cifras decimales A00796 y OEIS.
En ciencia e ingeniería, esta constante puede emplearse, la mayoría de las veces, con una precisión de sólo una docena de decimales. Con cincuenta decimales se podría describir con precisión la curvatura del Universo con un error más pequeño que el tamaño de un protón.[17]
[editar] Fórmulas que contienen el número π
[editar] En geometría
Áreas de secciones cónicas:
- Área del círculo de radio r: A = π r²
- Área de la elipse con semiejes a y b: A = π ab
Áreas de cuerpos de revolución:
Volúmenes de cuerpos de revolución:
- Volumen de la esfera de radio r: V = (4/3) π r³
- Volumen de un cilindro recto de radio r y altura h: V = π r² h
- Volumen de un cono recto de radio r y altura h: V = π r² h / 3
Ecuaciones expresadas en radianes:
- Ángulos: 180 grados son equivalentes a π radianes.
[editar] En probabilidad
- La probabilidad de que dos enteros positivos escogidos al azar sean primos entre sí es: 6/π²
- Si se eligen al azar dos números positivos menores que 1, la probabilidad de que junto con el número 1 puedan ser los lados de un triángulo obtusángulo es: (π-2)/4
- El número medio de formas de escribir un entero positivo como suma de dos cuadrados perfectos es π/4 (el orden es relevante).
- Aguja de Buffon: si lanzamos al azar una aguja de longitud L sobre una superficie en la que hay dibujadas líneas paralelas separadas una distancia D, la probabilidad de que la aguja corte a una línea es: Dπ/2L
[editar] En análisis matemático
[editar] Cómputos de π
[editar] Pi y los números primos
Utilizando el inverso del producto de Euler para la función zeta de Riemann y para el valor del argumento igual a 2 se obtiene:
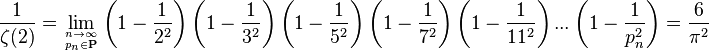
donde pn es el n-ésimo número primo. Euler fue el primero en hallar este valor de la función zeta (empleando la expresión de sumatoria) y resolviendo así el famoso Problema de Basilea.
[editar] Fórmula de Machin
Una forma exacta de poder calcular π en términos de tangentes inversas de fracciones unitarias es la fórmula de Machin, descubierta en 1706:
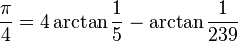
Muchos matemáticos emplearon esta fórmula para averiguar dígitos por encima de la centena (por ejemplo, el ya citado Shanks, que con esta fórmula calculó 707 posiciones decimales de π).
[editar] Métodos eficientes
Los primeros millones de dígitos de π y 1/π se pueden consultar en Proyecto Gutenberg (véase enlaces externos). Uno de los records más recientes fue alcanzado en diciembre de 2002 por Yasumasa Kanada de la Universidad de Tokio, fijando el número pi con 1.241.100.000.000 dígitos; se necesitaron unas 602 horas con un superordenador de 64 nodos Hitachi SR8000 con una memoria de un terabyte capaz de llevar a cabo 2 billones de operaciones por segundo, más de seis veces el record previo (206 mil millones de dígitos). Para ello se emplearon las siguientes fórmulas modificadas de Machin:
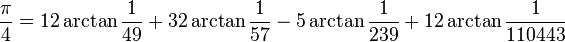
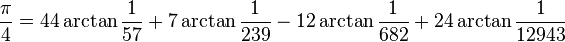
Estas aproximaciones proporcionaron una cantidad tan ingente de dígitos que puede decirse que ya no es útil sino para comprobar el funcionamiento de los superordenadores. La limitación no está en la computación sino en la memoria necesaria para almacenar una cadena con una cantidad tan grande de números.
[editar] Aproximaciones geométricas a π
Es posible obtener una aproximación al valor de π de forma geométrica. De hecho, ya los griegos intentaron obtener sin éxito una solución exacta al problema del valor de π mediante el empleo de regla y compás. El problema griego conocido como cuadratura del círculo o, lo que es lo mismo, obtener un cuadrado de área igual al área de un círculo cualquiera, lleva implícito el cálculo del valor exacto de π.
Una vez demostrado que era imposible la obtención de π mediante el uso de regla y compás, se desarrollaron varios métodos aproximados. Dos de las soluciones aproximadas más elegantes son las debidas a Kochanski (usando regla y compás) y la de Mascheroni (empleando únicamente un compás).
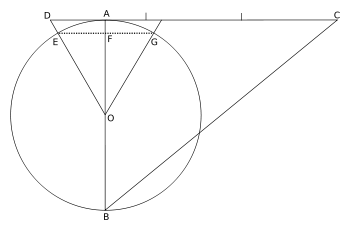
[editar] Método de Kochanski
Se dibuja una circunferencia de radio R. Se inscribe el triángulo equilátero OEG. Se traza una recta paralela al segmento EG que pase por A, prolongándola hasta que corte al segmento OE, obteniendo D. Desde el punto D y sobre ese segmento se transporta 3 veces el radio de la circunferencia y se obtiene el punto C. El segmento BC es aproximadamente la mitad de la longitud de la circunferencia.
Demostración (suponiendo R = 1)
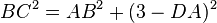
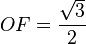
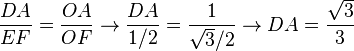
Sustituyendo en la primera fórmula:
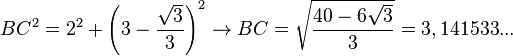
[editar] Método de Mascheroni
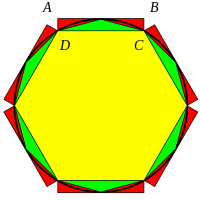
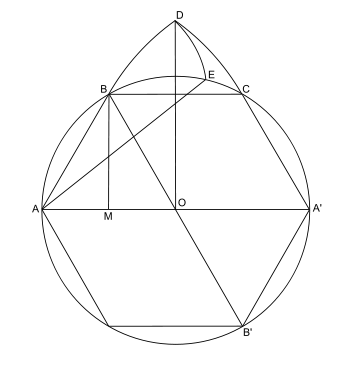
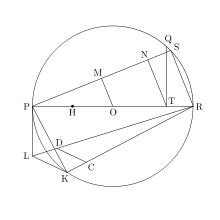
Método desarrollado por Lorenzo Mascheroni: se dibuja una circunferencia de radio R y se inscribe un hexágono regular. El punto D es la intersección de dos arcos de circunferencia: BD con centro en A', y CD con centro en A. Obtenemos el punto E como intersección del arco DE, con centro en B, y la circunferencia. El segmento AE es un cuarto de la longitud de la circunferencia, aproximadamente.
Demostración (suponiendo R = 1)
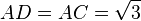
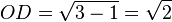
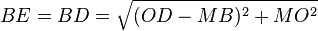
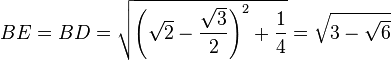
Por el teorema de Ptolomeo, en el cuadrilátero ABEB'
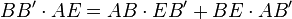
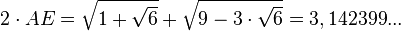
[editar] Uso en matemáticas y ciencia
π es ubicuo en matemáticas; aparece incluso en lugares que carecen de una conexión directa con los círculos de la geometría euclídea.[20]
[editar] Geometría y trigonometría
Para cualquier círculo de radio r y diámetro d = 2r, la longitud de la circunferencia es πd y el área del círculo es πr2. Además, π aparece en fórmulas para áreas y volúmenes de muchas otras figuras geométricas relacionadas con la circunferencia, como elipses, esferas, conos, y toroides.[21] π aparece en integrales definidas que describen la circunferencia, área o volumen de figuras generadas por circunferencias y círculos. En el caso básico, la mitad del área de un círculo unitario es:[22]
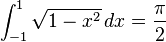
y la mitad de la longitud de la circunferencia unitaria es:[23]
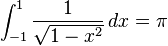
Se puede integrar formas más complejas como sólidos de revolución.[24]
De la definición de las funciones trigonométricas desde el círculo unitario se llega a que el seno y el coseno tienen período 2π. Lo que significa, para todo x y enteros n, sin(x) = sin(x + 2πn) y cos(x) = cos(x + 2πn). Porque sin(0) = 0, sin(2πn) = 0 para todos los enteros n. Además, el ángulo 180° es igual a π radianes. En otras palabras 1° = (π/180) radianes.
En matemáticas modernas, π es a menudo definido usando funciones trigonométricas, por ejemplo como el menor entero positivo x para el cual sinx = 0, para evitar dependencias innecesarias de las sutilezas de la geometría euclidiana y la integración. Equivalentemente, π puede ser definido usando funciones trigonométricas inversas, por ejemplo como π = 2 arccos(0) o π = 4 arctan(1). Expandir funciones trigonométricas inversas como series de potencias es la manera más fácil de obtener series infinitas para π.
[editar] Análisis superior y teoría de números
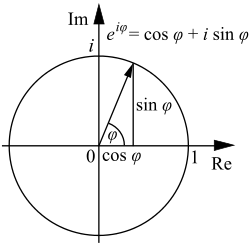
La frecuente aparición de π en análisis complejo puede estar relacionada con el comportamiento de la función exponencial de una variable compleja, descrito por la fórmula de Euler
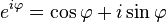
donde i es la unidad imaginaria que satisface la ecuación i2 = − 1 y e ≈ 2.71828 es el número de Euler. Esta fórmula implica que las potencias imaginarias de e describen rotaciones un círculo unitario en el plano complejo; estas rotaciones tienen un período de 360º = 2π. En particular, la rotación de 180º φ = π resulta en la notable identidad de Euler
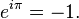
Hay n diferentes raíces n-ésimas de la unidad
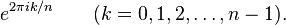
La integral de Gauss
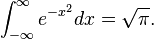
Una consecuencia es que el resultado de la división entre la función gamma de un semientero (la mitad de un número impar) y √π es un número racional.
Aunque no es una constante física, π aparece rutinariamente en ecuaciones que describen los principios fundamentales del Universo, Debido en gran parte a su relación con la naturaleza del círculo y, correspondientemente, con el sistema de coordenadas esféricas. Usando unidades como las unidades de Planck se puede eliminar a veces a π de las fórmulas.
[editar] Probabilidad y estadística
En probabilidad y estadística, hay muchas distribuciones cuyas fórmulas contienen a π, incluyendo:
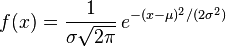
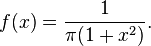
Nótese que para todas las funciones de densidad de probabilidad se cumple que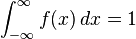 , entonces las fórmulas anteriores pueden usarse para producir otras fórmulas integrales para π.[32]
, entonces las fórmulas anteriores pueden usarse para producir otras fórmulas integrales para π.[32]
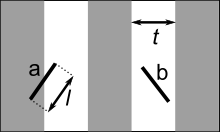
Representación del
experimento en el modelo de la "aguja de Buffon", se lanzas dos agujas (
a,
b) ambas con longitud
l. En el dibujo la aguja
a está cruzando la línea mientras que la aguja
b no.
El problema de la aguja de Buffon es llamado en ocasiones como una aproximación empírica de π. Se trata de lanzar una aguja de longitud l repetidamente sobre una superficie en la que se han trazado rectas paralelas distanciadas entre sí, en t unidades, de manera uniforme (con t > l de forma que la aguja no pueda tocar dos rectas). Si la aguja se lanza n veces y x de esas cae cruzando una línea, entonces se puede aproximar π usando el Método de Montecarlo, lanzándola gran cantidad de veces:[33] [34] [35] [36]
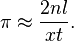
Aunque este resultado es matemáticamente impecable, no puede usarse más que para determinar unos cuantos dígitos de π experimentalmente. Para conseguirse sólo tres dígitos correctos (incluyendo el "3" inicial) requiere de millones de lanzamientos,[33] y el número de lanzamientos crece exponencialmente con el número de dígitos deseados. Además, cualquier error en la medida de las longitudes l y t se transfiere directamente como un error en la aproximación de π. Por ejemplo, una diferencia de un simple átomo en una aguja de 10 centímetros podría acarrear errores en el noveno dígito del resultado. En la práctica, incertidumbres en la determinación de si la aguja en realidad cruza una línea que parece estar solo tocándola lleva el límite de precisión alcanzable a mucho menos de 9 dígitos.
[editar] Curiosidades
[editar] Reglas mnemotécnicas
Es muy frecuente emplear poemas como regla mnemotécnica para poder recordar las primeras cifras del número pi.
- Una forma de memorizar los 20 primeros dígitos es con este poema, sólo hay que contar las letras de cada palabra:
Soy y seré a todos definible
mi nombre tengo que daros
cociente diametral siempre inmedible
soy de los redondos aros
- Otra versión, que permite enumerar los 27 primeros dígitos, es la siguiente:
"¿Qué? ¿Y cómo π reúne infinidad de cifras? ¡Tiene que haber períodos repetidos! Tampoco comprendo que de una cantidad poco sabida se afirme algo así, tan atrevido!" Nótese que para el segundo 1 (3,14159...) se utiliza la letra griega π.
- Un tercer poema:
Voy a amar a solas, deprimido
no sabrán jamás que sueño hallarte,
perímetro difícil, escondido
que en mis neuronas late...
Oscuro el camino para ver
los secretos que tú ocultas
¿hallarlos podré?...
- Otra regla, que permite recordar las primeras 32 cifras:
"Soy π, lema y razón ingeniosa de hombre sabio, que serie preciosa valorando, enunció magistral. Por su ley singular, bien medido el grande orbe por fin reducido fue al sistema ordinario usual."Aquí también se utiliza la letra griega π para el primer 1.
Existen cuentos amplios que son capaces de hacer memorizar una gran cantidad de dígitos, tal es el titulado "Cadaeic Cadenza", escrito en 1996 por el matemático Michael Keith y que ofrece la posibilidad de memorizar los primeros 3.834 dígitos. De esta forma, tomando "A" como 1, "B" como 2, "C" como 3, etc., el nombre de la historia saca los dígitos de pi, como "Cadaeic" es la primera palabra de 7 dígitos de pi:
C a d a e i c
3.1 4 1 5 9 3
Es de resaltar que en cada idioma existen diferentes reglas mnemotécnicas (se aconseja visitar cada Wikipedia para descubrir el arte empleado en cada idioma).
[editar] Aparición en medios
- En el año 1998 aparece una película del director Darren Aronofsky denominada Pi sobre un matemático que cree que el mundo se representa por números.
- Alfred Hitchcock en su film Cortina rasgada hace aparecer el símbolo π como una organización de espionaje.
- En La Película The Net, Aparece en la parte inferior derecho de una pagina de conciertos y música, de un programa llamado The Mozart Ghost, Aparentemente es solo un adorno, pero cuando se presiona CRTL+ALT+Click en π, se Accede a la interface de datos de el Guardián de la Puerta, un Programa de los Pretorianos, Que pedia un Usuario y un Password.
- En la serie de dibujos The Simpsons, en el episodio "Bye Bye Nerdie", el Professor Frink grita, a voz en cuello, que "¡π es igual a tres!", para atraer la atención de un auditorio compuesto por científicos. Cuando todos se dan vuelta para mirarlo, pide disculpas por haberse visto obligado a semejante sacrilegio.
- En la serie Futurama aparecen diferentes referencias a π, tales como 'aceite π en 1', y 'compre en πkea'.
- La novela Contacto de Carl Sagan —sobre la que luego se filmó la película homónima— toma a π (aunque no en base decimal) como un número que esconde la esencia misma del universo.
[editar] Datos interesantes

"Piso-Pi",
mosaico en la entrada del edificio de las matemáticas en TU
Berlín.

Detalle del "Mazda Pi", se añadieron 27 cifras decimales de π a este automóvil.
- El día 22 de julio (22/7) es el día dedicado a la aproximación de π.
- El 14 de marzo (3/14 en formato de fecha de Estados Unidos) se marca también como el día pi en el que los fans de este número lo celebran con diferentes actuaciones. Curiosamente es el cumpleaños de Einstein.
- 355/113 (~3.1415929) se menciona a veces como una simulación ¡cuasi-perfecta!
- Los usuarios del buscador A9.com que eligen su tienda virtual como amazon.com ofrecen descuentos de (π/2)% en sus compras.
- John Squire (de la banda The Stone Roses) menciona π en una canción escrita para su segunda banda The Seahorses denominada "Something Tells Me". La canción acaba con una letra como: "What's the secret of life? It's 3.14159265, yeah yeah!!".
- El primer millón de cifras de π y su inversa 1/π se puede consultar en el Proyecto Gutenberg o en este enlace.
- La numeración de las versiones del programa de tratamiento de texto TeX de Donald Knuth se realiza según los dígitos de π. La versión del año 2002 se etiquetó con 3.141592
- Se emplea este número en la serie de señales enviadas por la tierra con el objeto de ser identificados por una civilización inteligente extraterrestre.
- La probabilidad de que dos enteros positivos escogidos al azar sean primos entre si es 6 / π2
- Existen programas en internet que buscan tu número de teléfono en las 50.000.000 primeras cifras de π
- En algunos lenguajes de programación se pueden averiguar tantos dígitos como se desee con simplemente emplear expresiones como: RealDigits[ N[ Pi, 105]] en «Mathematica».
- En el año 2002 el japonés Akira Haraguchi rompió el record mundial recitando durante 13 horas 83.431 dígitos del número pi sin parar, doblando el anterior record en posesión del también japonés Hiroyuki Goto. El 4 de octubre de 2006, a la 1:30 de la madrugada, y tras 16 horas y media, Haraguchi volvió a romper su propio record recitando 100.000 dígitos del número pi, realizando una parada cada dos horas de 10 minutos para tomar aire.
- El máximo número de dígitos de π necesario para buscar cualquier secuencia de día-mes-año con cuatro dígitos en la expansión decimal de pi es 60.872.
- Existe una canción de Kate Bush llamada "Pi" en la cual se recitan más de veinte dígitos decimales del número.
- En Argentina, el número telefónico móvil para emergencias en estaciones de trenes y subterráneos es ∗31416.[37]
- El valor principal de la expresión ii es un número real y está dado por[38]
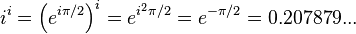
- En la página web thinkgeek.com pueden comprarse camisetas y accesorios con π. En el enlace se puede ver una camiseta en la que se construye la letra π con sus primeros 4493 digitos.[39] [40]
- Existe un vehículo Mazda 3 modificado, al que se le añadieron 27 cifras de π, después del 3.[41]
- Srinivasa Ramanujan publicó una solución aproximada, con regla y compás, a la cuadratura del círculo en 1913 en la que obtuvo un segmento aproximadamente igual a
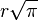 :[42]
:[42]
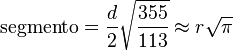
[editar] Días de Aproximación a Pi
Según determinadas coincidencias numéricas, los Días de Aproximación a Pi son:
[editar] Cuestiones abiertas sobre π
- Cada uno de los dígitos decimales 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9, ¿tiene una aparición infinita en los decimales de π?
- La denominada cuestión de Brouwer: en la expansión decimal de π, ¿existe alguna posición donde exista una sucesión de mil ceros consecutivos?
- ¿Es π simplemente normal en base 10? Es decir, ¿tiene cada uno de los diez dígitos del sistema decimal la misma probabilidad de aparición en una expansión decimal?
- No se sabe si π+e, π/e , ln(π) son irracionales. Se sabe que no son raíces de polinomios de grado inferior a ocho y con coeficientes enteros del orden 109.[43] [44]
[editar] Referencias
- ↑ G L Cohen and A G Shannon, John Ward's method for the calculation of pi, Historia Mathematica 8 (2) (1981), 133-144
- ↑ New Introduction to Mathematics, William Jones, 1706, London
- ↑ Gay Robins y Charles Shute: The Rhind Mathematical Papyrus: an ancient Egyptian text, British Museum Publications, London , 1987, véase “Squaring the Circle”, páginas 44 a 46.
- ↑ "The Exact Sciences in Antiquity", Otto Neugebauer, 1957, Dover, New York ,(nueva edición de 1969).
- ↑ Petr Beckmann: A History of Pi, publicado por primera vez por The Golem Press, 1971, edición consultada por Barnes and Noble Books, New York , 1993.
- ↑ a b c Bailey DH, Borwein JM, Borwein PB, y Plouffle S, "The quest for Pi", The Mathematical Intelligencer 19 (1997), pp. 50-57.
- ↑ A. Volkov, Calculation of π in ancient China: from Liu Hui to Zu Chongzhi, Historia Sci. (2) 4 (2) (1994), 139-157
- ↑ a b c Boyer Carl (1999). Historia de la Matemática. Madrid : Alianza Editorial. 84-206-8186-5.
- ↑ O'Connor, John J.; Robertson, Edmund F., «Biografía de Liu Hui» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Liu_Hui.html
- ↑ C. Jami, Une histoire chinoise du 'nombre π', Archive for History of Exact Sciences 38 (1) (1988), 39-50
- ↑ Arndt J., Haenel C. Pi unleashed (trad. de C. y D. Lischka). Berlin, Nueva York: Springer, 2001, p. 188 y 228. ISBN: 978-3-540-66572-4
- ↑ a b c d e Bailey David H. , Some Background on Kanada’s Recent Pi Calculation (2003). Disponible en este enlace. Consultada:22 de abril de 2008
- ↑ Yomiuri Online, 17 de agosto de 2009, «円周率計算で世界一…筑波大がギネス申請» (en japonés)
- ↑ Pi Computation Record, por Fabrice Bellard (en inglés)
- ↑ Euclides, Elementos. Libro V
- ↑ Mahler, K. "On the Approximation of ." Nederl. Akad. Wetensch. Proc. Ser. A. 56/Indagationes Math. 15, 30-42, 1953.
- ↑ Bailey, David H., Borwein, Peter B., and Borwein, Jonathan M. (January 1997). "The Quest for Pi". Mathematical Intelligencer (1): 50-57.
- ↑ Existen otras doce representaciones de π en http://functions.wolfram.com/Constants/Pi/10/
- ↑ Calculation of Pi Using the Montecarlo Method
- ↑ «Japonés rompe el récord de memorizar cifras de pi». BBC News (2 de febrero de 2005). Consultado el 30-10-2007.
- ↑ «Área y circunferencia de un Círculo de Arquímedes». Penn State. Consultado el 08-11-2007.
- ↑ Weisstein, Eric W (28 de enero de 2006). «Unit Disk Integral». MathWorld. Consultado el 08-11-2007.
- ↑ «Area and Circumference of a Circle by Archimedes». Penn State. Consultado el 08-11-2007.
- ↑ Weisstein, Eric W (4 de mayo de 2006). «Solid of Revolution». MathWorld. Consultado el 08-11-2007.
- ↑ Miller, Cole. «The Cosmological Constant» (PDF). University of Maryland. Consultado el 08-11-2007.
- ↑ Imamura, James M (2005-08-17). «Heisenberg Uncertainty Principle». University of Oregon. Consultado el 09-11-2007.
- ↑ Einstein, Albert (1916). «The Foundation of the General Theory of Relativity» (PDF). Annalen der Physik. http://www.alberteinstein.info/gallery/gtext3.html.
- ↑ Nave, C. Rod (2005-06-28). «Coulomb's Constant». HyperPhysics. Georgia State University. Consultado el 09-11-2007.
- ↑ «Magnetic constant». NIST (2006 CODATA recommended values). Consultado el 09-11-2007.
- ↑ Weisstein, Eric W. «Gaussian Integral» (en inglés). MathWorld. Wolfram Research. Consultado el 08-11-2007.
- ↑ Weisstein, Eric W. «Cauchy Distribution» (en inglés). MathWorld. Wolfram Research. Consultado el 08-11-2007.
- ↑ Weisstein, Eric W. «Probability Function» (en inglés). MathWorld. Wolfram Research. Consultado el 08-11-2007.
- ↑ a b Weisstein, Eric W. «Buffon's Needle Problem» (en inglés). MathWorld. Wolfram Research. Consultado el 10-11-2007.
- ↑ Bogomolny, Alexander. «Math Surprises: An Example» (en inglés). Interactive Mathematics Miscellany and Puzzles. Consultado el 28-10-2007.
- ↑ Ramaley, J. F. (Oct 1969). «Buffon's Noodle Problem». The American Mathematical Monthly 76 (8): pp. 916-918.
- ↑ «The Monte Carlo algorithm/method». datastructures (2007-01-09). Consultado el 07-11-2007.
- ↑ Plan de seguridad para el subte Artículo del diario Clarín
- ↑ Unidad imaginaria en Mathworld [1] (en inglés). consulta: 21 de abril de 2008
- ↑ Camisetas de pi en gaussianos.com. Consultado: 23 de abril de 2008.
- ↑ Página de ventas de camisetas pi en thinkgeek.com. Consultado: 23 de abril de 2008
- ↑ "Mazda Pi" en Gaussianos.com. Consultado: 23 de abril de 2008
- ↑ Ramanujan, Srinivasa (1913). «Squaring the circle» (djvu). Journal of the Indian Mathematical Society. http://en.wikisource.org/wiki/Squaring_the_circle.
- ↑ Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving π, e and Euler's Constant." Math. Comput. 50, 275-281, 1988a.
- ↑ Pi en Mathworld [2] (en inglés). consulta: 21 de abril de 2008
[editar] Véase también
[editar] Enlaces externos
Obtenido de "http://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80"
 Investigadores de la Universidad de California han diseñado un ojo similar al de los insectos para lograr una visión de gran angular. El nuevo ojo permitirá nuevas aplicaciones en intervenciones quirúrgicas, en la industria, etc.
Investigadores de la Universidad de California han diseñado un ojo similar al de los insectos para lograr una visión de gran angular. El nuevo ojo permitirá nuevas aplicaciones en intervenciones quirúrgicas, en la industria, etc.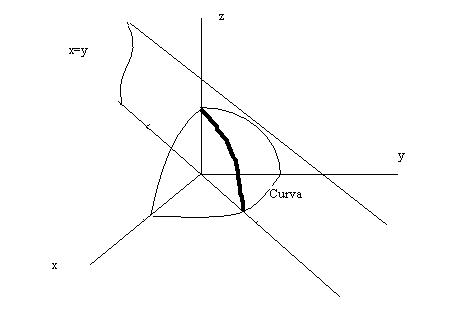
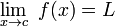
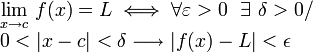
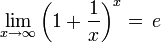 (
(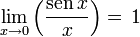
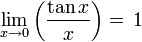
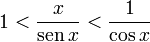
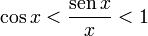
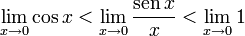
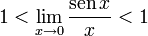
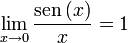
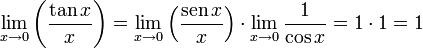

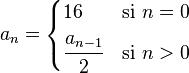
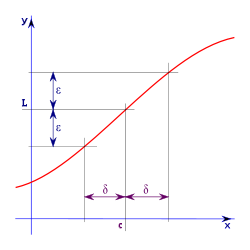
 . Decimos que la sucesión
. Decimos que la sucesión 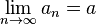
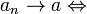
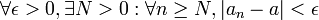
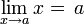
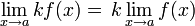 donde k es un multiplicador
donde k es un multiplicador 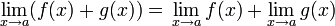
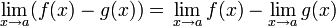
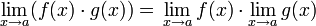
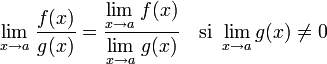
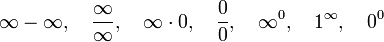
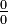 es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :
es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :![lim_{trightarrow 0}frac{t}{t^2}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0}frac{1}{t} = infty](https://petalofucsia.blogia.com/upload/externo-2c2a8339dc5ed8ccd290f53129017bc9.png)
![lim_{trightarrow 0}frac{t}{t}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0} 1 =1](https://petalofucsia.blogia.com/upload/externo-c974cdd467d4b4aca64166c24df85228.png)
![lim_{trightarrow 0}frac{t^2}{t}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0} {t} = 0](https://petalofucsia.blogia.com/upload/externo-90fc66d0f750b2fd989ffd86b93fe625.png)


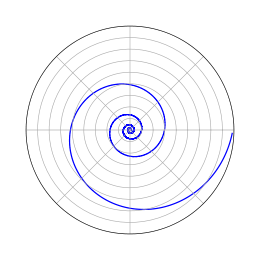
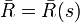 , siendo s el arco, quiere decir que existe un vector unitario
, siendo s el arco, quiere decir que existe un vector unitario 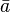 fijo tal que para todo s se verifica
fijo tal que para todo s se verifica 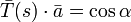 (constante).
(constante).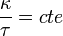 , siendo tanα la constante.
, siendo tanα la constante.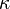 es la
es la 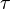 la
la 







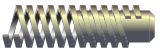



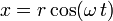
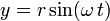
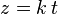
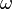 es el ángulo girado por unidad de tiempo, t es el tiempo y k es el avance en el sentido z por unidad de tiempo.
es el ángulo girado por unidad de tiempo, t es el tiempo y k es el avance en el sentido z por unidad de tiempo.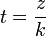
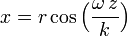
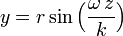
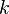 son valores conocidos y constantes, podemos definir:
son valores conocidos y constantes, podemos definir: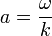
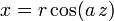
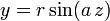

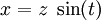
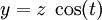
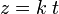
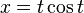
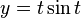
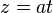
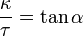 (constante), o lo que es lo mismo
(constante), o lo que es lo mismo 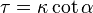 .
.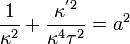 (constante).
(constante).
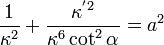
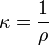 , se obtiene:
, se obtiene: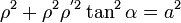 , o lo que es lo mismo, :
, o lo que es lo mismo, :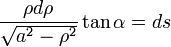
 .
.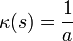 y por tanto
y por tanto 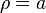 .
. se obtiene
se obtiene 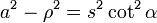 .
.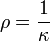 , será:
, será: 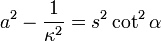
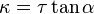 , resulta:
, resulta: 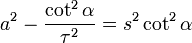 , y por tanto:
, y por tanto: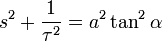
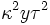 se obtiene:
se obtiene: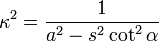
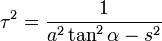
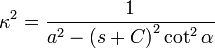
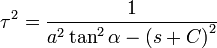





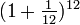 = 2,61303...UMs. Por tanto, cada vez que se aumenta la cantidad de períodos de pago en un factor de n (que tiende a crecer sin límite) y se reduce la tasa de interés en el período, en un factor de
= 2,61303...UMs. Por tanto, cada vez que se aumenta la cantidad de períodos de pago en un factor de n (que tiende a crecer sin límite) y se reduce la tasa de interés en el período, en un factor de 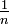 , el total de unidades monetarias obtenidas está expresado por la siguiente ecuación:
, el total de unidades monetarias obtenidas está expresado por la siguiente ecuación: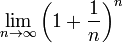
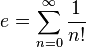
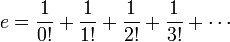
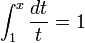
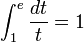
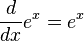
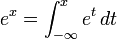
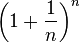
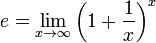
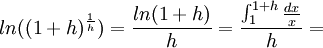
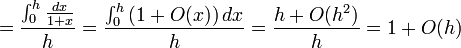
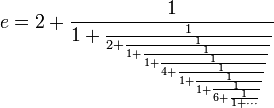
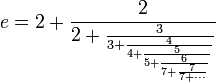
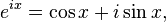
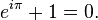
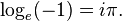
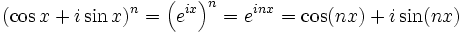
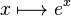
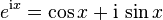 . Un caso particular de esta relación es la
. Un caso particular de esta relación es la 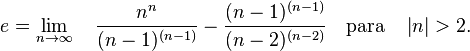
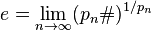
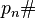 es el
es el 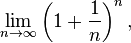
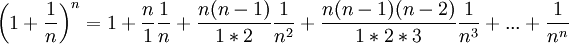
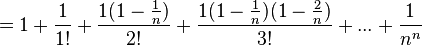
 , como se quería demostrar.
, como se quería demostrar.
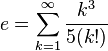
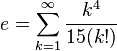
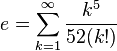
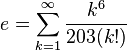
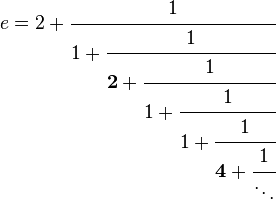
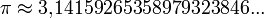

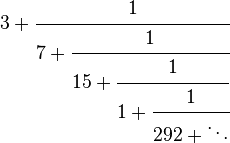


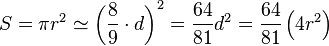
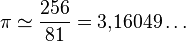

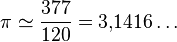
 , que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo
, que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo 

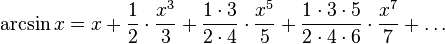
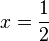 obtuvo una serie para
obtuvo una serie para 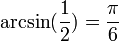 .
.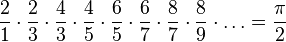 .
.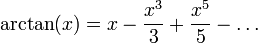
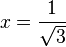 se obtiene una serie para
se obtiene una serie para 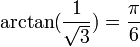 . Para alcanzar la precisión obtenida, debió usar alrededor de trescientos términos en la serie. En 1720 el francés
. Para alcanzar la precisión obtenida, debió usar alrededor de trescientos términos en la serie. En 1720 el francés 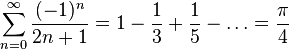 .
.
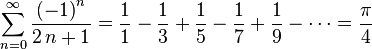
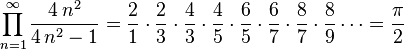
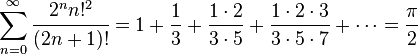
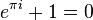
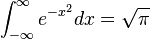
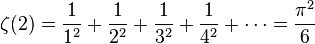
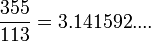
![sqrt[29] {261424513284461} approx pi](https://petalofucsia.blogia.com/upload/externo-1797fc6ce9446a0c45ce41faff2bb507.png)
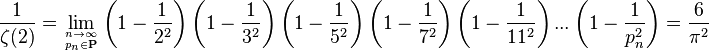
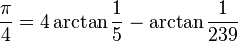
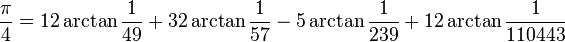
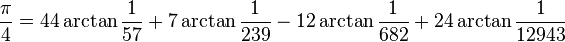
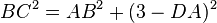
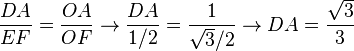
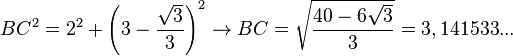
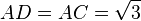
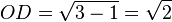
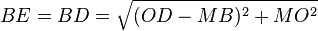
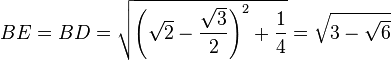
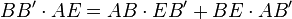
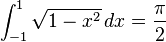
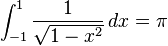
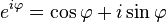
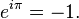
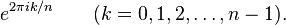
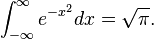
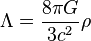
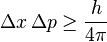
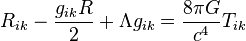
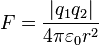
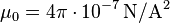
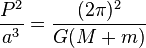
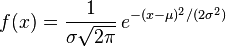
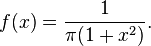
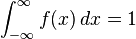 , entonces las fórmulas anteriores pueden usarse para producir otras fórmulas integrales para π.
, entonces las fórmulas anteriores pueden usarse para producir otras fórmulas integrales para π.
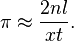



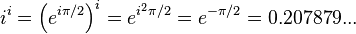
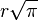 :
: