CIENCIA7: ¿DETERMINISMO O INDETERMINISMO? PREDICTIBILIDAD. UNA de las más grandes metas de la ciencia es ser capaz de predecir fenómenos. Veamos con un poco de detalle lo que esto significa.

X. ¿DETERMINISMO O INDETERMINISMO?

PREDICTIBILIDAD

UNA de las más grandes metas de la ciencia es ser capaz de predecir fenómenos. Veamos con un poco de detalle lo que esto significa.

Después de investigar a fondo un fenómeno específico, se han podido establecer los mecanismos que rigen este fenómeno. Por ejemplo, el caso del movimiento de los planetas alrededor del Sol fue estudiado por Newton, quien demostró que, si hay una fuerza entre cuerpos que tienen masa, dada por la ley de la gravitación universal que propuso, entonces, de acuerdo con sus leyes de movimiento los planetas deberían girar alrededor del Sol en elipses. Newton estableció ciertas ecuaciones matemáticas que describen el fenómeno y, a partir de la solución de sus ecuaciones, encontró las elipses. Es decir, Newton pudo hacer una predicción. Esta forma de proceder se llama en física construir un modelo. De alguna forma este modelo refleja matemáticamente las características físicas del sistema: en este caso, de la relación entre los planetas y el Sol.

Pero esto no es todo. Por medio de sus resultados Newton pudo considerar lo siguiente: si se llega a saber dónde se encuentra un planeta en determinado momento, se podrá saber dónde estará en cualquier otro instante de tiempo. Es decir, si se conocen las condiciones iniciales del planeta se puede determinar su trayectoria en el futuro. Aplicadas estas ideas al movimiento del cometa Halley, este científico inglés predijo en el siglo XVIII, que el cometa debería regresar cada 76 años, hecho que en efecto ha ocurrido; las dos últimas apariciones fueron en 1910 y en 1986.

Sin embargo, para poder especificar las condiciones iniciales es necesario medirlas con algún aparato. Como resultado de la medición de cualquier cantidad se obtiene un número. Pero este número contiene incertidumbres, ya que en el proceso de medición en que lo obtenemos hay factores que, en general, no se pueden controlar. Por ejemplo, si se mide el peso de un cuerpo con una balanza, pueden ocurrir errores en la lectura de la aguja, debido a alguna vibración que produzca el paso de un vehículo, o a causa de alguna corriente de aire, etc. Es decir, siempre que se mide algo hay errores. Por tanto, como resultado de una medición se debe dar el número obtenido así como los límites de los errores que se puedan cometer.

Así, por ejemplo, como resultado de una medición de peso se dirá que el peso del cuerpo de interés se encuentra entre 54.5 kg y 54.8 kg. El "verdadero" valor del peso está dentro de este intervalo. El intervalo:

 

54.8 kg - 54.5kg = 0.3kg

es un cálculo del error cometido al hacer la medición.

Por supuesto que mientras menores sean los errores que se cometan, mejor será el resultado de la medición. Lo más que se puede hacer es lograr que el intervalo dentro del cual caen las mediciones disminuya, pero no se puede eliminar.

En general, podemos afirmar que no se puede hacer una medición con precisión absoluta. Siempre se tendrá un intervalo de error dentro del cual cae el "verdadero" valor. Los límites de error experimental son estimaciones cuantitativas de la importancia de las perturbaciones que muchos factores externos, prácticamente imposibles de controlar, provocan en la medición. La determinación del intervalo de error experimental es parte del trabajo cotidiano de un científico experimental. Mientras menor sea el intervalo de error, más precisa será la medición efectuada.

Como consecuencia del hecho de que una medición contiene errores, ocurre lo siguiente: supongamos que se lanza hacia abajo una piedra desde 7 m de altura sobre el suelo (figura 21(a)) y queremos predecir dónde estará la piedra después de 2 segundos. Si tenemos un modelo necesitaremos introducir las condiciones iniciales; en este caso, una es la altura sobre el suelo. Supóngase que al medir la posición inicial de la piedra se encuentra que los errores experimentales la sitúan entre los puntos A y B de la figura, con un intervalo de 0.12cm. El modelo que se tiene puede entonces predecir que después de 2 segundos, la piedra se encontrará a una altura de 1.5 m sobre el suelo. Ahora supondremos que se produce una de las dos situaciones siguientes:

1) La piedra deberá estar en un intervalo de 0.14 cm entre los puntos C y D (figura 21(b))

2) La piedra deberá estar en un intervalo de 2.15 cm entre los puntos C y D (figura 21(c)).

Si el modelo con el que se trabaja da lugar a los resultados del inciso (2) entonces no se puede hablar de que el modelo predice dónde estará la piedra después de 2 segundos, ya que los límites de error se magnificaron: de 0.12 cm a 2.15 cm. Este resultado casi nos dice que la piedra puede estar, después de 2 segundos, en cualquier lugar. Claramente esto no es lo que llamaríamos una predicción.

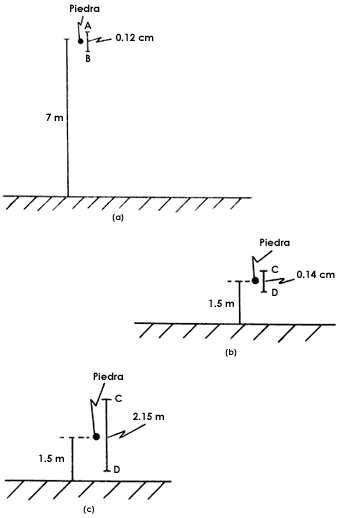
Figura 21. Al transcurrir el tiempo, el error inicial en la determinación de la posición de la piedra (a) puede quedar dentro de un intervalo análogo al inicial (b) o puede crecer mucho (c).

Por otro lado, en el caso del inciso (1) vemos que los errores se mantuvieron muy parecidos a los de la determinación inicial. Se considera que en este caso el modelo ha predicho la posición de la piedra. No es posible hacer una mejor predicción.

Si se hace un experimento para determinar la posición de la piedra, los límites de error deberán ser análogos a los hechos en el momento en que se determinó la posición inicial.

En consecuencia, si los parámetros del sistema que se está considerando son tales que la propagación de los errores no se amplifica, entonces el modelo sí predice el comportamiento futuro del sistema (éste sería el caso del inciso (1)). Si ocurre que los límites de error se amplifican (como en el caso del inciso (2)), entonces el modelo no es capaz de predecir el comportamiento futuro del sistema.

Ahora trataremos esta cuestión de la predicción para el caso que se consideró en el capítulo VIII, es decir, la forma en que evoluciona una población dada por la ecuación (6) , es decir, para el caso no lineal.

Consideremos el caso de q = 2.5 y tratemos dos condiciones iniciales muy cercanas: 0.25 y 0.27. A continuación presentamos las primeras iteraciones:

 

Valor inicial = 0.25	Valor inicial = 0.27	Diferencia
0.4688	0.4928	0.0240
0.6226	0.6229	0.0003
0.5874	0.5860	0.014
0.6059	0.6065	0.0006
0.5970	0.5966	0.0004
0.6015	0.6017	0.0002
0.5992	0.5992	0.0000
0.6004	0.6004	0.0000
0.5998	0.5998	0.0000
0.6001	0.6001	0.0000
0.6000	0.5999	0.0001
0.6000	0.6000	0.0000

 

 

En la última columna se presenta el cálculo de la diferencia entre los valores de cada renglón.

Se puede observar que, en primer lugar, la diferencia entre los valores iniciales es 0.27 - 0.25 = 0.02. En segundo lugar, si se observa la columna de diferencias podemos afirmar que éstas nunca son mayores que 0.02, la diferencia inicial (excepto en el primer renglón, en que es de 0.024, que es parecido a 0.02), sino que disminuyen a medida que progresamos en la iteración hasta que finalmente son prácticamente nulas. Esto último es una manifestación de algo que ya conocemos. No importa cuales sean las condiciones iniciales, para el caso de q = 2.5, siempre se terminará con el valor final de 0.6. En consecuencia, en este caso el modelo sí es capaz de hacer una predicción, ya que los límites de error iniciales no se amplifican, sino que prácticamente se llega al mismo resultado (0.6) sin importar cuál haya sido el valor inicial de la población.

Por otro lado, supóngase que el valor de q es igual a 3.6 y se tratan dos condiciones iniciales, por ejemplo, 0.60 y 0.63; si uno se pregunta cuáles son las poblaciones en las iteraciones 98, 99 y 100, se obtienen los siguientes valores:

 

Valor inicial = 0.60	Valor inicial = 0.63	Diferencia
0.3413	0.4567	0.1154
0.8094	0.8932	0.0838
0.5555	0.3433	0.2122

 

En primer lugar, vemos que la diferencia entre los valores iniciales es 0.63 - 0.60 = 0.03. En segundo lugar observamos que para estas iteraciones, las diferencias no son del mismo tamaño que la inicial. Estas diferencias llegan a ser mucho mayores que 0.03 y además son muy variables, la primera es de 0.1154, luego es 0.0838 y enseguida crece fuertemente a 0.2122. Podemos afirmar entonces que si la situación es tal que q =3.6, los límites de error iniciales no nada más se amplifican, sino que se vuelven azarosos. Por tanto, en este caso el modelo no es capaz de predecir la situación futura de la poblacion.

Del análisis de estos dos casos concluimos que: a) el modelo es capaz de hacer predicciones, en el sentido que arriba mencionamos, si los parámetros del sistema (en nuestro caso el valor de q) son tales que ocurre un comportamiento periódico, y b) que el modelo no es capaz de hacer predicciones si los parámetros son tales que se está en la región caótica.

Por otro lado nos damos cuenta de que, para cualquier valor del parámetro q, la regla para hacer iteraciones está completamente determinada. Esto significa que el modelo es determinista. si uno da el valor de q y la condición inicial de x, siempre obtendrá el mismo valor para la iteración 127, digamos. En consecuencia, este modelo es determinista y presenta dos tipos de regímenes: el periódico y el caótico. Puede parecer a primera vista que hay una contradicción entre estos términos. Sin embargo, como se ha ilustrado, éste no es el caso.

En este punto conviene hacer una aclaración muy importante. El modelo constituye la descripción de una parte de la naturaleza: puede ser descrito en términos matemáticos o no. Así el modelo dado en el capítulo VIII trata de representar un fenómeno, el de la variación de la población de insectos. El modelo es el que puede ser determinista o no, puede ser caótico o no. En nuestro caso el modelo sí es determinista, porque se puede determinar cuantas veces se quiera el valor de la población en el instante que se quiera (o sea la iteración que se quiera) habiendo dado el parámetro q y la condición inicial de x.

No hay que confundir entre el modelo que trata de representar a cierta realidad con la realidad misma.

Se ha ilustrado un hecho muy importante. Un modelo determinista, como el de la ecuación (6), en ciertas condiciones de los valores de los parámetros (por ejemplo q) puede predecir el comportamiento futuro y los errores en las condiciones iniciales no se amplifican. En otras condiciones, para otros valores de los parámetros, el modelo no puede predecir el comportamiento futuro; ahora los errores en las condiciones iniciales se amplifican y además el comportamiento se vuelve azaroso. En el primer caso (donde sí se pueden hacer predicciones) el sistema está en un régimen periódico. En el segundo caso (donde no se pueden hacer predicciones) el sistema está en un régimen caótico. Nótese que ambos tipos de comportamientos ¡se dan en el mismo sistema!

Obtenido de http://bibliotecadigital.ilce.edu.mx/sites/ciencia/volumen3/ciencia3/150/htm/sec_12.htm