CIENCIA5: DIMENSIONES. La dimensión (del latín dimensio, "medida") es, esencialmente, el número de grados de libertad para realizar un movimiento en el espacio. Comúnmente, las dimensiones de un objeto son las medidas que definen su forma y tamaño.
Dimensión
La dimensión (del latín dimensio, "medida") es, esencialmente, el número de grados de libertad para realizar un movimiento en el espacio. Comúnmente, las dimensiones de un objeto son las medidas que definen su forma y tamaño.
Contenido[ocultar] |
[editar] Dimensiones físicas
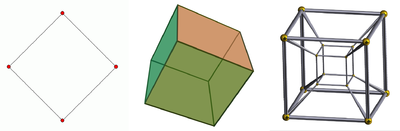
El espacio en el que vivimos parece de cuatro dimensiones. Tradicionalmente, se separa en tres dimensiones espaciales y una dimensión temporal (y en la mayoría de los casos es razonable y práctico). Podemos movernos hacia arriba o hacia abajo, hacia el norte o sur, este u oeste, y los movimientos en cualquier dirección puede expresarse en términos de estos tres movimientos. Un movimiento hacia abajo es equivalente a un movimiento hacia arriba de forma negativa. Un movimiento norte-oeste es simplemente una combinación de un movimiento hacia el norte y de un movimiento hacia el oeste.
El tiempo, a menudo, es «la cuarta dimensión». Es diferente de las tres dimensiones espaciales ya que sólo hay uno, y el movimiento parece posible sólo en una dirección. En el nivel macroscópico los procesos físicos no son simétricos con respecto al tiempo. Pero, a nivel subatómico (escala de Planck), casi todos los procesos físicos son simétricos respecto al tiempo (es decir, las ecuaciones utilizadas para describir estos procesos son las mismas independientemente de la dirección del tiempo), aunque esto no significa que las partículas subatómicas puedan regresar a lo largo del tiempo.
La Teoría de las cuerdas predice que el espacio en que vivimos tiene muchas más dimensiones (10, 11 o 26), pero que el universo medido a lo largo de estas dimensiones adicionales tiene tamaño subatómico.
En las ciencias físicas y la ingeniería, del tamaño de una magnitud física es la expresión del tipo de unidades de medida en que esta cantidad se expresa. La dimensión de la velocidad, por ejemplo, resulta de dividir la longitud entre el tiempo. En el sistema SI, las dimensiones vienen dadas por siete magnitudes fundamentales relacionadas con las características físicas fundamentales.
[editar] Dimensiones matemáticas
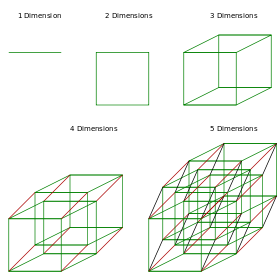
En matemáticas, no existe una definición de dimensión que incluya de manera adecuada todas las situaciones. En consecuencia, los matemáticos han elaborado muchas definiciones de dimensión para los diferentes tipos de espacio. Todas, sin embargo, están en última instancia, basadas en el concepto de la dimensión de un espacio euclídeo n, E n. El punto E 0 es 0-dimensional. La línea E 1 es 1-dimensional. El plano E 2 es 2-dimensional. En general, E n es n-dimensional.
[editar] Dimensión de un espacio vectorial
Un espacio vectorial sobre un cuerpo que se dice que tiene dimensión si existe una base de cardinal n. En un espacio vectorial, todas las bases tienen el mismo cardinal, lo que hace de la dimensión el primer invariante del álgebra lineal. El espacio vectorial trivial {0} tiene como dimensión 0 porque el conjunto vacío es su base: una combinación de cero vector da el vector nulo.
Intuitivamente hablando, la dimensión de un espacio vectorial nos dice cuántos elementos necesitamos para poder expresar cualquier elemento del espacio en términos de las combinaciones lineales de los primeros, i.e., cuántos elementos del espacio necesitamos para poder expresar todos los elementos del espacio como sumas de múltiplos de éstos elementos.
[editar] Dimensión topológica
La dimensión topológica es la que nos resulta más intuitiva y pragmática para comprender. Esta establece la dimensión de un punto = 0, la de una línea = 1, la de una superficie = 2, etc.
Más formalmente escrito, un objeto tiene dimensión topológica m cuando cualquier recubrimiento de ese objeto, tiene como mínimo una dimensión topológica = m+1 (estableciendo previamente que el punto tiene dimensión topológica = 0).
Aún más formalmente: la definición para conjuntos con dimensión topológica 0 queda como sigue: se dice que un conjunto F tiene dimensión topológica 0, DT(F)=0, si y sólo si para todo x perteneciente a F y cualquier conjunto abierto U (para la topología relativa de F) que contenga a x, existe un abierto V tal que x pertenece a V que está incluido en U y la frontera de V con la intersección a F es vacía.
[editar] Dimensión fractal de Hausdorff-Besicovitch
Esta dimensión es comúnmente confundible con la entropía de Kolmogórov o la dimensión de Minkowski Bouligand. La dimensión de Hausdorff-Besicovitch se obtiene como un punto de inflexión del valor de la potencia elegida en la longitud de Hausdorff cuando esta pasa de ser infinita a ser nula. La longitud de Hausdorff es la suma del diámetro topológico elevado a una potencia "s" de un recubrimiento entero del objeto a partir de entornos o cubrimientos de diámetro delta o menor a este del propio objeto.
[editar] La entropía de Kolmogórov
Se denomina entropía de Kolmogórov a una dimensión obtenida para facilidad de cálculos como el cociente logarítmico entre el número de homotecias internas encontradas en un objeto por transformación, y la inversa de la razón de esa homotecia. Es también llamada Box Counting Dimension y tiene una definición más intuitiva pero más larga al respecto.
Es de esta manera que los objetos euclidianos diferenciables se ven con una correspondencia en su valor dimensional topológica, de Box Counting y de H.B.
Esto no resulta con los fractales, donde son definidos por Benoit Mandelbrot como:
Objetos tales que su dimensión de Hausdorff - Besicovitch excede estrictamente su dimensión topológica.Finalmente sabemos que existen casos de fractales que no se apegan a esta definición; una de esas es la curva del Diablo, la cual es un fractal derivado del conjunto de Cantor.
[editar] En ciencia ficción
En ciencia ficción, a veces se usa el término "dimensión" como sinónimo de universo paralelo; aunque el término este relacionado no son sinónimos (véase teoría de las cuerdas).
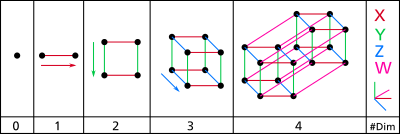
0 comentarios