CIENCIA4: LO PARANORMAL, ¿NÚMEROS IRRACIONALES? ¿POSIBILIDADES DE UNA NUEVA CIENCIA AQUÍ? En matemáticas, un número irracional es cualquier número real que no es racional, es decir, es un número que no puede ser expresado como una fracción , donde m y n son enteros, con n diferente de cero y donde esta fracción es irreducible.

12 de octubre de 2010 - 14:13 - Ciencia4

Número irracional

De Wikipedia, la enciclopedia libre

En matemáticas, un número irracional es cualquier número real que no es racional, es decir, es un número que no puede ser expresado como una fracción 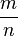$frac{m}{n}$ , donde $m$ y $n$ son enteros, con $n$ diferente de cero y donde esta fracción es irreducible.

[editar] Notación

A veces ^[¿quién?] se denota por 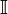$mathbb{I}$ al conjunto de los Números Irracionales. Esta notación no es universal y muchos matemáticos^[¿quién?] la rechazan. Las razones son que el conjunto de Números Irracionales no constituyen ninguna estructura algebraica, como sí lo son los Naturales ( 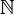$mathbb{N}$ ), los Enteros ( 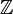$mathbb{Z}$ ), los Racionales ( 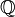$mathbb{Q}$ ), los Reales ( 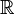$mathbb{R}$ ) y los Complejos ( 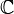$mathbb{C}$ ), por un lado, y que la $mathbb{I}$ es tan apropiada para designar al conjunto de Números Irracionales como al conjunto de Números Imaginarios Puros, lo cual puede crear confusión.

[editar] Clasificación

Tras distinguir los números componentes de la recta real en tres categorías: (naturales, enteros y racionales), podría parecer que ha terminado la clasificación de los números, pero aun quedan "huecos" por rellenar en la recta de los números reales. Los números irracionales son los elementos de dicha recta que cubren los vacíos que dejan los números racionales.

Los números irracionales son los elementos de la recta real que no pueden expresarse mediante el cociente de dos enteros y se caracterizan por poseer infinitas cifras decimales que no siguen un periodo definido. De este modo, puede definirse al número irracional como decimal infinito no periódico. En general, toda expresión en números decimales es solo una aproximación en números racionales al número irracional referido, por ejemplo, el número racional 1,4142135 es solo una aproximación a 7 cifras decimales del número irracional raíz cuadrada de 2, el cual posee infinitas cifras decimales que no siguen un periodo.

Entonces, decimos con toda propiedad que el número raíz cuadrada de dos es aproximadamente igual a 1,4142135 en 7 decimales, o bien es igual a 1,4142135 ... , es decir, los tres puntos hacen referencia a los infinitos decimales que hacen falta y que jamás terminaríamos de escribir.

Debido a ello, los números irracionales más conocidos son identificados mediante símbolos especiales; los tres principales son los siguientes:

$π$ (Número "pi" 3,1415 ...): razón entre la longitud de una circunferencia y su diámetro.
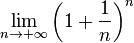
e (Número "e" 2,7182 ...): $lim _{n to +infty} left( 1 + frac {1}{n}right) ^{n}$
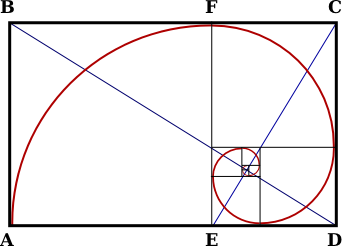
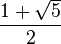
$Φ$ (Número "áureo" 1,6180 ...): $frac{1 + sqrt{5}}{2}$

Los números irracionales se clasifican en dos tipos:

1.- Número algebraico: Son la solución de alguna ecuación algebraica y se representan por un número finito de radicales libres o anidados; si "x" representa ese número, al eliminar radicales del segundo miembro mediante operaciones inversas, queda una ecuación algebraica de cierto grado. Todas las raíces no exactas de cualquier orden son irracionales algebraicos.

Por ejemplo, el número áureo es una de las raíces de la ecuación algebraica:

$x 2 - x - 1 = 0$ , por lo que es un número irracional algebraico.

2.- Número trascendente: No pueden representarse mediante un número finito de raíces libres o anidadas; provienen de las llamadas funciones trascendentes: trigonométricas, logarítmicas y exponenciales. También surgen al escribir números decimales no periódicos al azar o con un patrón que no lleva periodo definido, respectivamente, como los dos siguientes:

0,193650278443757 ...

0,101001000100001 ...

Los llamados números trascendentes tienen especial relevancia ya que no pueden ser solución de ninguna ecuación algebraica. Los números pi y e son irracionales trascendentes, puesto que no pueden expresarse mediante radicales.

Los números irracionales no son numerables, es decir, no pueden ponerse en biyección con el conjunto de los números naturales. Por extensión, los números reales tampoco son contables ya que incluyen el conjunto de los irracionales.