HISTORIA10: ¿QUÉ PASA SI ORDENAMOS LOS NOMBRES DE ACUERDO CON LAS PROGRESIONES?. Una sucesión geométrica está constituida por una secuencia de elementos en la que cada uno de ellos se obtiene multiplicando el anterior por una constante denominada razón o factor de la progresión. Se suele reservar el término progresión cuando la secuencia tiene una cantidad finita de términos mientras que se usa sucesión cuando hay una cantidad infinita de términos, si bien, esta distinción no es estricta.
Progresión geométrica
Una sucesión geométrica está constituida por una secuencia de elementos en la que cada uno de ellos se obtiene multiplicando el anterior por una constante denominada razón o factor de la progresión. Se suele reservar el término progresión cuando la secuencia tiene una cantidad finita de términos mientras que se usa sucesión cuando hay una cantidad infinita de términos, si bien, esta distinción no es estricta.
Así, 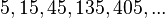 es una progresión geométrica con razón igual a 3, porque:
es una progresión geométrica con razón igual a 3, porque:
y así sucesivamente.
Aunque es más fácil aplicando la fórmula:
Siendo 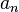 el término en cuestión,
el término en cuestión, 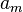 el primer término y
el primer término y  la razón:
la razón:
Así quedaría si queremos saber el 6º término de nuestra progresión
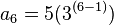
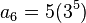
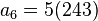
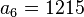
Contenido[ocultar] |
[editar] Ejemplos de progresiones geométricas
- La progresión 1, 2 ,4 ,8 ,16, es una progresión geométrica cuya razón vale 2, al igual que 5, 10, 20, 40.
- La razón no necesariamente tiene que ser un número entero. Así, 12, 3, 0.75, 0.1875 es una progresión geométrica con razón 1/4.
- La razón tampoco tiene porqué ser positiva. De este modo la progresión 3, -6, 12, -24 tiene razón -2. Este tipo de progresiones es un ejemplo de progresión alternante porque los signos alternan entre positivo y negativo.
- Cuando la razón es igual a 1 se obtiene una progresión constante: 7, 7, 7, 7
- Un caso especial es cuando la razón es igual a cero, por ejemplo: 4, 0, 0, 0. Existen ciertas referencias que no consideran este caso como progresión y piden explícitamente que
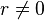 en la definición.
en la definición.
[editar] Suma de términos de una progresión geométrica
[editar] Suma de los primeros n términos de una progresión geométrica
Se denomina como Sn a la suma de n términos consecutivos de una progresión geométrica:
Sn = a1 + a2 + ... + an-1 + anSi se quiere obtener una fórmula para calcular de una manera rápida dicha suma, se multiplica ambos miembros de la igualdad por la razón de la progresión r.
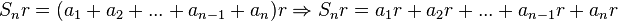
Si se tiene en cuenta que al multiplicar un término de una progresión geométrica por la razón se obtiene el término siguiente de esa progresión,
Sn r = a2 + a3 + ... + an + an rSi se procede a restar de esta igualdad la primera:
Sn r = a2 + a3 + ... + an + an rSn = a1 + a2 + ... + an-1 + an_______________________________Sn r - Sn = - a1 + an ro lo que es lo mismo,
Sn ( r - 1 ) = an r - a1Si se despeja Sn,
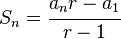
De esta manera se obtiene la suma de los n términos de una progresión geométrica cuando se conoce el primer y el último término de la misma. Si se quiere simplificar la fórmula, se puede expresar el término general de la progresión an como
an = a1 rn-1Así, al sustituirlo en la fórmula anterior se tiene lo siguiente:
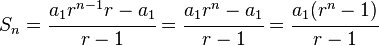
con lo que se obtiene la siguiente igualdad:
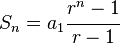
Con esta fórmula se puede obtener la suma de n términos consecutivos de una progresión geométrica con sólo saber el primer término a sumar y la razón de la progresión.
Si queremos calcular el resultado de una suma de n términos consecutivos, pero sin que empiece en cero, debemos utilizar la expresión:
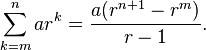
[editar] Suma de términos infinitos de una progresión geométrica
Si el valor absoluto de la razón es menor que la unidad | r | < 1, la suma de los infinitos términos decrecientes de la progresión geométrica converge hacia un valor finito. En efecto, si | r | < 1, 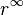 tiende hacia 0, de modo que:
tiende hacia 0, de modo que:
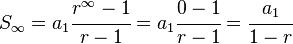
En definitiva, la suma de los infinitos términos de una progresión geométrica de razón inferior a la unidad se obtiene utilizando la siguiente fórmula:
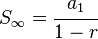
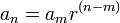
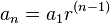
0 comentarios