MATEMÁTICAS: CONJUNTO (ESCATOLOGÍA). En matemáticas, un conjunto es un concepto fundamental , y como tal no admite definición en términos de conceptos más fundamentales.[1] A veces se lo presenta como un concepto autoevidente, o por medio de sinónimos. Por ejemplo, a veces se dice que un conjunto es una colección de objetos.[1] Por objeto aquí no debe entenderse sólo las entidades físicas, como las mesas y las sillas, sino todo objeto en el sentido más amplio de la palabra: mesas, sillas, personas, ideas, creencias, lenguajes, letras, otros conjuntos, etc. A los objetos que pertenecen a un conjunto se los llama miembros o elementos del conjunto.

13 de mayo de 2010 - 16:31 - Matemáticas

Conjunto

De Wikipedia, la enciclopedia libre

CONJUNTOS FRACTALES:

Conjuntos.

En matemáticas, un conjunto es un concepto fundamental , y como tal no admite definición en términos de conceptos más fundamentales.^[1] A veces se lo presenta como un concepto autoevidente, o por medio de sinónimos. Por ejemplo, a veces se dice que un conjunto es una colección de objetos.^[1] Por objeto aquí no debe entenderse sólo las entidades físicas, como las mesas y las sillas, sino todo objeto en el sentido más amplio de la palabra: mesas, sillas, personas, ideas, creencias, lenguajes, letras, otros conjuntos, etc. A los objetos que pertenecen a un conjunto se los llama miembros o elementos del conjunto.

Otras veces se toma a los axiomas de la teoría de conjuntos como proveyendo una definición implícita de lo que es un conjunto: un conjunto es todo aquello que cumple con los axiomas.^[1] Sin embargo, esto conlleva el riesgo de que haya más de una interpretación que haga verdaderos a los axiomas (más de un modelo), y por lo tanto de que haya más de un definiendum

La cantidad de elementos de un conjunto puede ser finita o infinita.^[2] Por ejemplo, el conjunto de los números naturales, que son infinitos, es un conjunto tanto como el conjunto de los planetas del Sistema Solar, que son ocho.

En un conjunto, el orden de los elementos es irrelevante.^[2] El conjunto compuesto por Venus y Mercurio es el mismo que el compuesto por Mercurio y Venus. También es irrelevante si se repite un elemento.^[2] Venus y Mercurio forman el mismo conjunto que Mercurio y Venus.

Los conjuntos no deben ser confundidos con los agregados. Los primeros son estudiados por la teoría de conjuntos, los segundos por la mereología. Los primeros son siempre entidades abstractas, los segundos no siempre. Por ejemplo, el conjunto de todas las personas no tiene ningún peso, pero el agregado de todas las personas sí.

Contenido

[ocultar]

Determinación de un conjunto [editar]

Un conjunto se puede determinar de dos maneras: por extensión y por comprensión

Por extensión [editar]

Un conjunto está determinado por extensión cuando se escriben uno a uno todos sus elementos. Por ejemplo, el conjunto de los números naturales menores que 9:

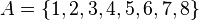
$A = {1, 2, 3, 4, 5, 6, 7, 8 } ,$

Por comprensión [editar]

Un conjunto está determinado por comprensión cuando solamente se menciona una característica común de todos los elementos. Por ejemplo, el conjunto formado por las letras vocales del abecedario:

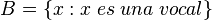
$B = {x: x ; es ; una ; vocal } ,$

Dos conjuntos son idénticos si, y sólo si, contienen los mismos elementos. Se puede obtener una descripción más detallada en la teoría de conjuntos.

Las aplicaciones de teoría de conjuntos son muy amplias, y baste con mencionar que se utiliza en el diseño de circuitos en electrónica digital; en cuestiones relacionadas con probabilidad; y sus conceptos están de manera implícita en la terminología utilizada en diseño de bases de datos, cuando se realizan las consultas. conjuntos de varios elementos.y esta determinado por comprension y por extension

Representación de un conjunto [editar]

A es subconjunto de B.

Unión de A y B.

Intersección de A y B.

Los conjuntos son uno de los conceptos básicos de la matemática. Como ya se ha dicho, un conjunto es, más o menos, una colección de objetos, denominados elementos. La notación estándar utiliza llaves {, y } alrededor de la lista de elementos para indicar el contenido del conjunto, como por ejemplo:

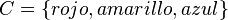
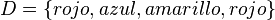
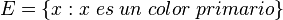
$C = {rojo, amarillo, azul } ,$ $D = {rojo, azul, amarillo, rojo } ,$ $E = {x: x ; es ; un ; color ; primario } ,$

Las tres líneas anteriores denotan el mismo conjunto. Como puede verse, es posible describir el mismo conjunto de diferentes maneras: o bien dando un listado de sus elementos (lo mejor para conjuntos finitos pequeños) o bien dando una propiedad que defina todos sus elementos. Por otro lado, no importa el orden, ni cuantas veces aparezcan en la lista sus elementos.

Si A y B son dos conjuntos y todo elemento x de A está contenido también en B, entonces se dice que A es un subconjunto de B. Todo conjunto tiene como subconjunto a sí mismo y al conjunto vacío, {}.

La unión de una colección de conjuntos: 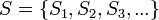$S= { S_1 , S_2 , S_3 , ... } ,$ es el conjunto de todos los elementos contenidos al menos una vez en los conjuntos 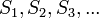$S_1 , S_2 , S_3 , ... ,$ y se representa: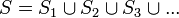 $S= S_1 cup S_2 cup S_3 cup ... ,$

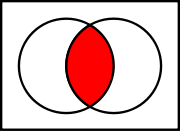
La intersección de una colección de conjuntos: 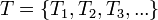$T= { T_1 , T_2 , T_3 , ... } ,$ , es el conjunto de todos los elementos contenidos simultáneamente en todos los conjuntos: 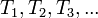$T_1 , T_2 , T_3 , ... ,$ y se representa: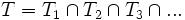 $T= T_1 cap T_2 cap T_3 cap ... ,$

los conjuntos también son nombrados según el número de elementos que tengan ejemplo conjunto vacío, conjunto unitario,conjunto finito,conjunto infinito. Algunos ejemplos de conjuntos de números son:

Los números naturales utilizados para contar los elementos de un conjunto.
Los números enteros.
Los números racionales.
Los números reales, que incluyen a los números irracionales.
Los números complejos que proporcionan soluciones a ecuaciones del tipo: $x 2 + 1 = 0$ .

La teoría estadística se construye sobre la base de la teoría de conjuntos y la teoría de la probabilidad.

Relaciones entre conjuntos [editar]

Una categoría matemática consta de dos partes: los objetos y los morfismos. Cuando hablamos de la categoría de conjuntos, los objetos son los mismos conjuntos y un morfismo $f$ entre dos objetos, digamos $X$ e $Y$ , en un tipo de relación entre $X$ e $Y$ dirigida i.e. un subconjunto del producto cartesiano de $X$ con $Y$ , en símbolos:

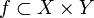
$f subset X times Y$

y ésta es una aplicación entre los conjuntos. conjunto de varios elementos y esta determinado por extension y por comprension.

Véase también [editar]

conjunto de varios elementos y esta determinado por comprension y por extension.

Notas y referencias [editar]

↑ ^a ^b ^c Jech, Thomas, «Set Theory», en Edward N. Zalta (en inglés), The Stanford Encyclopedia of Philosophy (Spring 2009 Edition edición), http://plato.stanford.edu/archives/spr2009/entries/set-theory/, consultado el 7 de octubre de 2009
↑ ^a ^b ^c Weisstein, Eric W., «Set» (en inglés), MathWorld, http://mathworld.wolfram.com/Set.html, consultado el 7 de octumbre de 2009

Obtenido de "http://es.wikipedia.org/wiki/Conjunto"

Categoría oculta: Wikipedia:Artículos destacados en w:lmo