CIENCIA2: ESPACIO EUCLÍDEO. El espacio euclídeo o euclidiano es el espacio matemático n-dimensional usual, una generalización de los espacios de 2 (plano euclídeo) y 3 dimensiones estudiados por Euclides. El término "espacio euclídeo n-dimensional" es usualmente abreviado a "n-espacio euclídeo", o sólo "n-espacio". El n-espacio euclídeo se denota por E n, aunque ℝn es bastante usado (sobreentendiendo la métrica). E 2 se dice el plano euclídeo.
Espacio euclídeo
De Wikipedia, la enciclopedia libre

| Este artículo o sección tiene un nivel técnico muy alto para lectores que no son expertos en el tema. Si tienes capacidad, por favor edítalo, contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a los especialistas. |
El espacio euclídeo o euclidiano es el espacio matemático n-dimensional usual, una generalización de los espacios de 2 (plano euclídeo) y 3 dimensiones estudiados por Euclides.
El término "espacio euclídeo n-dimensional" es usualmente abreviado a "n-espacio euclídeo", o sólo "n-espacio". El n-espacio euclídeo se denota por E n, aunque ℝn es bastante usado (sobreentendiendo la métrica). E 2 se dice el plano euclídeo.
Contenido[ocultar] |
Introducción [editar]
Estructuralmente un espacio euclídeo es un espacio vectorial normado sobre los números reales de dimensión finita, en que la norma es la asociada al producto escalar ordinario. Para cada número entero no negativo n, el espacio euclídeo n-dimensional es el conjunto:
junto con la función distancia obtenida mediante la siguiente definición de distancia entre dos puntos (x1, ..., xn) e (y1, ...,yn):
Esta función distancia está basada en el teorema de Pitágoras y es llamada Distancia euclidiana.
Estructuras sobre el espacio euclídeo [editar]
Los espacios euclídeos y sus propiedades han servido de base para generar gran cantidad de conceptos matemáticos relacionados con la geometría, la topología, el álgebra y el cálculo. Aunque el espacio euclídeo suele ser introducido por razones como espacio vectorial, en realidad sobre él se pueden definir muchas más estructuras. El espacio euclídeo es además de un espacio vectorial un caso de:
- Un espacio de Hilbert de dimensión finita, con el producto escalar ordinario.
- Un espacio de Banach de dimensión finita, con norma inducida por el producto escalar anterior.
- Un espacio métrico completo, con distancia inducida por la norma anterior.
- Un espacio topológico, inducido por la métrica euclídea.
- Un grupo de Lie, con la operación de adición.
- Un álgebra de Lie con el producto vectorial.
El espacio euclídeo como espacio métrico [editar]
Por definición, E n es un espacio métrico, y es por tanto también un espacio topológico; es el ejemplo prototípico de una n-variedad, y es de hecho una n-variedad diferenciable. Para n ≠ 4, cualquier n-variedad diferenciable que sea homeomorfa a E n es también difeomorfa a ella. El hecho sorprendente es que esto no es cierto también para n = 4, lo que fue probado por Simon Donaldson en el año 1982; los contraejemplos se llaman 4-espacios exóticos (o falsos).
El espacio euclídeo como espacio topológico [editar]
Se puede decir mucho sobre la topología de E n, Pero esperaremos a una próxima edición de este artículo. Un resultado importante, el invariancia del dominio de Brouwer, es el de que cualquier subconjunto de E n que sea homeomorfo a un subconjunto abierto de E n es en sí mismo abierto. Como consecuencia inmediata de esto se tiene que E m no es homeomorfo a E n si m ≠ n -- un resultado intuitivamente "obvio" que sin embargo no es fácil de demostrar.
El espacio euclídeo como espacio vectorial [editar]
El n-espacio euclídeo se puede considerar también como un Espacio vectorial n-dimensional real, de hecho un Espacio de Hilbert, de manera natural. El producto interior, también llamado producto punto, de x = (x1,...,xn) e y = (y1,...,yn) está dado por
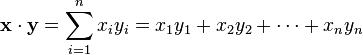
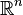
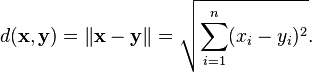
0 comentarios