LÓGICA FRENTE A PENSAMIENTO MÁGICO: GENIALIDAD: GEOMETRÍA DIFERENCIAL DE CURVAS. En matemáticas, la geometría diferencial de curvas propone definiciones y métodos para analizar curvas simples en Variedades de Riemann, y en particular, en el Espacio Euclídeo.
Geometría diferencial de curvas
De Wikipedia, la enciclopedia libre

En matemáticas, la geometría diferencial de curvas propone definiciones y métodos para analizar curvas simples en Variedades de Riemann, y en particular, en el Espacio Euclídeo.
Contenido[ocultar] |
Longitud de arco [editar]
Dada una curva suficientemente suave (diferenciable y de clase 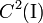 ), en
), en 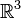 y dado su vector de posición
y dado su vector de posición 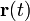 expresado mediante el parámetro t;
expresado mediante el parámetro t;
![mathbf{r}(t)=x(t)mathbf i+y(t)mathbf j+z(t)mathbf k qquad t in [a,b] ,](https://petalofucsia.blogia.com/upload/externo-ab2f751bd54808d67e2e4746d16fd55b.png)
se define el llamado parámetro de arco s como:
![s =phi(t)= int_{a}^{t} sqrt{left [ x'(tau) right ] ^2 + left [ y'(tau)right ]^2 + left [z'(tau)right ] ^2} , dtau](https://petalofucsia.blogia.com/upload/externo-8b1930bda814ef532fec68d36b2b96ee.png)
La cual se puede expresar también de la siguiente forma en la cual resulta más fácil de recordar
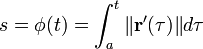
Lo cual permite reparametrizar la curva de la siguiente manera:
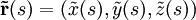
donde
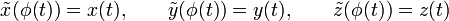
son las relaciones entre las dos parametrizaciones.
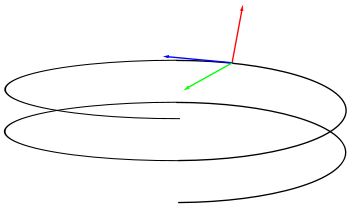
Vectores tangente, normal y binormal: Triedro de Frênet-Serret [editar]
Dada una curva parametrizada r(t) según un parámetro cualquiera t se define el llamado vector tangente, normal y binormal como:
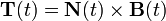 ó bien
ó bien 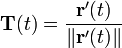
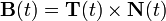 ó bien
ó bien 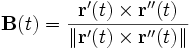
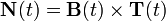 ó bien
ó bien ![mathbf{N}(t)=frac{[mathbf{r}'(t)times mathbf{r}''(t)]times mathbf{r}'(t)}{left Vert [mathbf{r}'(t)times mathbf{r}''(t)]times mathbf{r}'(t) right |}](https://petalofucsia.blogia.com/upload/externo-020881fcb80a6e1de822ea827a9c92f0.png)
Estos tres vectores son unitarios y perpendiculares entre sí, juntos configuran un sistema de referencia móvil conocido como Triedro de Frênet-Serret a raiz del estudio de Jean Frenet y Joseph Serret. Es interesante que para una partícula física desplazándose en el espacio, el vector tangente es paralelo a la velocidad, mientras que el vector normal da el cambio dirección por unidad de tiempo de la velocidad o aceleración normal.
Si la curva está parametrizada según la longitud de arco, como se explicó en la sección anterior las fórmulas anteriores pueden simplificarse notablemente:
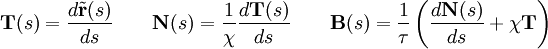
Donde la curvatura y la torsión son precisamente los parámetros χ y τ anteriores.
Curvatura y torsión [editar]
La curvatura es una medida del cambio de dirección del vector tangente a una curva, cuanto más rápido cambia éste a medida que nos desplazamos a lo largo de la curva, se dice, que más grande es la curvatura. Para una curva parametrizada cualquiera la curvatura es igual a:
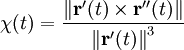
Si la curva está parametrizada por el parámetro de longitud de arco, la anterior ecuación se reducen a:
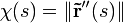
Además de la curvatura se suele definir el llamado radio de curvatura, como el inverso de la curvatura.
La torsión es una medida del cambio de dirección del vector binormal: cuanto más rápido cambia, más rápido gira el vector binormal alrededor del vector tangente y más retorcida aparece la curva. Por lo tanto, para una curva totalmente contenida en el plano la torsión es nula ya que el vector binormal es constantemente perpendicular al plano que la contiene. Para el caso general la torsión viene dada por:
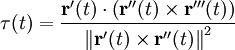
Si la curva está parametrizada por el parámetro de longitud de arco, la anterior ecuación se reduce simplemente a:
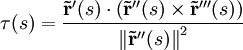
Plano osculador [editar]
El plano osculador es el plano que contiene en cada punto de la curva a su vector tangente y a su vector normal. Para una partícula desplazándose en el espacio el plano osculador coincide con el plano que en cada instante contiene a la aceleración y la velocidad. La ecuación de este plano viene dada por:
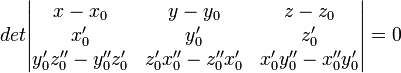
Donde: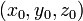 , el punto de la trayectoria.
, el punto de la trayectoria.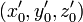 , el vector velocidad en el punto considerado.
, el vector velocidad en el punto considerado.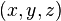 , las coordenadas de un punto genérico del plano osculador.
, las coordenadas de un punto genérico del plano osculador.
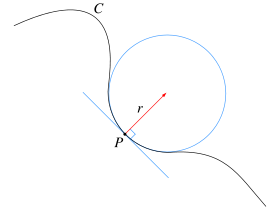
Centro de curvatura [editar]
En un entorno de un punto de una curva puede ser aproximado por un círculo, llamado círculo osculador por estar contenido en el plano osculador. El radio del círculo osculador coincide con el radio de curvatura (inverso de la curvatura). El centro de dicho círculo puede buscarse como:
O más sencillamente en función del parámetro de arco como:
Teorema fundamental de curvas [editar]
El teorema fundamental de curvas que enunciamos a continuación nos dice que conocido un punto de una curva y su vector tangente, la curva queda totalmente especificada si se conoce la función de curvatura y de torsión. Su enunciado es el siguiente:
Sea 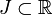 un intervalo. Dadas dos funciones continuas χ y τ de
un intervalo. Dadas dos funciones continuas χ y τ de 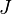 a
a 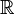 y dado un sistema de referencia fijo (ortonormal) de
y dado un sistema de referencia fijo (ortonormal) de 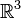 , {x0; e1, e2, e3}, entonces existe una única curva parametrizada de
, {x0; e1, e2, e3}, entonces existe una única curva parametrizada de 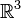 ,
,  y tales que:
y tales que:
- La curva pasa por x0, y el vector tangente T a la curva en ese punto coincide con e1.
- A lo largo de la curva pueden definirse tres campos vectoriales T(s), N(s) y B(s) llamados respectivamente vector tangente, normal y binormal, perpendiculares entre sí y tales que en el punto inicial coinciden con e1, e2, e3 (es decir, T(0) = e1, N(0) = e2, B(0) = e3).
- Se cumplen las siguientes ecuaciones:
O bien escrito matricialmente
donde el punto es la derivada con respecto al arcoparámetro s.
Esto tiene implicaciones físicas interesantes, por ejemplo, la trayectoria de una partícula queda especificada si se conocen la posición inicial, la velocidad inicial y la variación en el tiempo de las derivadas segundas (que están relacionadas con la curvatura y la torsión). Es por eso por lo que las leyes de Newton o las ecuaciones de Euler-Lagrange se expresan en términos de derivadas de segundo orden (que es necesario complementar con la posición y velocidades iniciales).
Véase también [editar]
Bibliografía [editar]
- Girbau, J.: "Geometria diferencial i relativitat", Ed. Universitat Autònoma de Barcelona, 1993. ISBN 84-7929-776-X.
- Spiegel, M. & Abellanas, L.: "Fórmulas y tablas de matemática aplicada", Ed. McGraw-Hill, 1988. ISBN 84-7615-197-7.
Enlaces externos [editar]
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática.
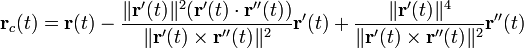
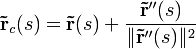
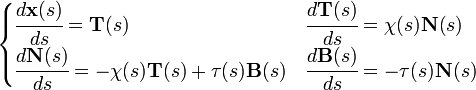
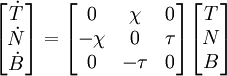
0 comentarios