MATEMÁTICAS3: SINGULARIDADES. Dentro de la amplia variedad de funciones matemáticas existentes se encuentran algunas que presentan comportamientos extraños e inesperados cuando se le asignan determinados valores a la/s variable/s independiente/s. Dicho comportamiento se describe con el nombre de singularidad de la función.
Singularidad matemática
Dentro de la amplia variedad de funciones matemáticas existentes se encuentran algunas que presentan comportamientos extraños e inesperados cuando se le asignan determinados valores a la/s variable/s independiente/s. Dicho comportamiento se describe con el nombre de singularidad de la función.
Contenido[ocultar] |
[editar] Concepto intuitivo de continuidad
Intuitivamente se asocia la idea de continuidad de una función al hecho de no levantar el lápiz cuando se representa gráficamente la función. Las discontinuidades generalmente se clasifican en varios tipos, siendo las llamadas de salto uno de los tipos más frecuentes. Dentro de dicho tipo existen las discontinuidades de salto puntuales, en las que la función se desvía un único punto del camino más razonable; las discontinuidades de salto finito, en las cuales la función salta un valor y prosigue de forma continua a partir de ahí; y por último las discontinuidades de salto infinito, en las que la función alcanza un valor infinito. Estas últimas son las que reciben el nombre de singularidades.
Criterio de análisis de continuidad en funciones de una variable:
Una función 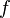 es continua en
es continua en 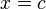 si y sólo si:
si y sólo si:
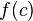 está definido.
está definido.- Existe el límite de
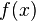 cuando
cuando 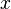 tiende a
tiende a  .
. - El límite de
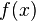 cuando
cuando 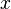 tiende a
tiende a  coincide con
coincide con 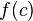 .
.
[editar] Funciones singulares
Existe una gran variedad de funciones elementales que contienen singularidades en sus dominios. Una de las más comunes suele ser la hipérbola elemental 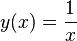 . Esta función posee una singularidad en el punto
. Esta función posee una singularidad en el punto 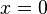 , en dicho punto la función presenta un comportamiento que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función
, en dicho punto la función presenta un comportamiento que tiende al infinito. Dicha función pone de manifiesto la carácterística de que toda función racional cuyo denominador se anule presentará una singularidad en el punto en el que eso suceda. así pues la función 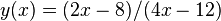 presentará una singularidad en el punto
presentará una singularidad en el punto 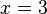 . Otras funciones que contienen singularidades son
. Otras funciones que contienen singularidades son 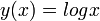 ó
ó 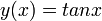 .
.
[editar] Análisis de las singularidades
Normalmente las singularidades no pueden estudiarse empleando técnicas aritméticas elementales, ya que suelen implicar operaciones que son imposibles de realizar (por ejemplo, dividir por cero). En lugar de eso, el método preferido para analizar el comportamiento de las funciones en sus singularidades es el paso al límite. Estudiando el límite de una función en su punto singular se puede obtener información valiosa de su comportamiento en ese punto. Como ejemplo comentar que nadie puede calcular que y(x) = 1 / x toma en el punto x = 0 el valor infinito, sin embargo, estudiando el valor que toma su límite en ese punto y analizando la tendencia de la función en las cercanías es posible asegurarlo.
[editar] Singularidades en variable compleja
Sea 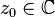 , y una función
, y una función 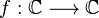 se dice que f(z) es singular en z0 si no es analítica en z0.
se dice que f(z) es singular en z0 si no es analítica en z0.
Además, si z0 es una singularidad de f(z), decimos que es una singularidad no aislada si 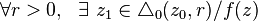 es singular en z1. Es decir, a una distancia arbitraria, sigo encontrando otra singularidad. z0 es una singularidad aislada, si z0 es una singularidad y no es no aislada. Dentro de las singularidades aisladas, las podemos clasificar en:
es singular en z1. Es decir, a una distancia arbitraria, sigo encontrando otra singularidad. z0 es una singularidad aislada, si z0 es una singularidad y no es no aislada. Dentro de las singularidades aisladas, las podemos clasificar en:
- Evitables: Puede definirse un valor tal que f(z) sea analitica en z0.
- Polares: f(z) tiende a
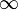 al acercarse a z0.
al acercarse a z0.
- Esenciales: El límite no es independiente del camino, y aún más, la función toma valores por todo el plano complejo (excepto uno) en un entorno a z0 y lo hace infinitas veces.
Es posible estudiar el tipo de singularidad no aislada, mediante el desarrollo de Laurent en la corona centrada en z0. Si la serie principal (la de potencias negativas) tiene finitos términos, se trata de una singularidad polar, caso contrario, es esencial. Lógicamente se desprende, que si el desarrollo de Laurent se reduce a una serie de Taylor, la singularidad es evitable.
[editar] Interpretación física de las singularidades
El estudio de las singularidades desde el punto de vista matemático se limita especificamente a resolver el problema de la función que no está definida en el punto de estudio. Sin embargo, desde el punto de vista físico el estudio de las singularidades es a menudo más apasionante.
Teorías tales como el electromagnetismo clásico de Maxwell contienen singularidades en sus ecuaciones básicas. En la teoría de Maxwell una de las singularidades más conocidas es la que predice un campo eléctrico infinito en el lugar donde se encuentra colocada una carga puntual.
Una de las singularidades más famosas de la física es la que se encuentra en la solución de Schwarzschild de las ecuaciones de campo de la relatividad general, singularidad en el continuo espacio-tiempo que predice la existencia de agujeros negros.
Actualmente uno de los campos de discusión abiertos más apasionante de la física es aquel que pretende estudiar si hubo o no singularidad en el principio del universo y si la habrá en el final del mismo.
0 comentarios