CIENCIA5: EL NÚMERO e. ¿ESTÁ PRESENTE EN EL LENGUAJE?. La constante matemática e es uno de los más importantes números reales.[1] Se relaciona con muchos interesantes resultados. Por ejemplo, la derivada de la función exponencial f(x) = ex es esa misma función. El logaritmo en base e se llama logaritmo natural o neperiano.
Número e

La constante matemática e es uno de los más importantes números reales.[1] Se relaciona con muchos interesantes resultados. Por ejemplo, la derivada de la función exponencial f(x) = ex es esa misma función. El logaritmo en base e se llama logaritmo natural o neperiano.
El número e, conocido a veces como número de Euler o constante de Napier, fue reconocido y utilizado por primera vez por el matemático escocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.
Está considerado el número por excelencia del cálculo, así como π lo es de la geometría e i del análisis complejo. El simple hecho de que la función ex coincida con su derivada hace que la función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas. Como consecuencia de esto, describe el comportamiento de acontecimientos físicos regidos por leyes sencillas, como pueden ser la velocidad de vaciado de un depósito de agua, el giro de una veleta frente a una ráfaga de viento, el movimiento del sistema de amortiguación de un automóvil o el cimbreo de un edificio metálico en caso de terremoto. De la misma manera, aparece en muchos otros campos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos (descarga de un condensador, amplificación de corrientes en transistores BJT, etc.), biológicos (crecimiento de células, etc.), químicos (concentración de iones, periodos de semidesintegración, etc.), y muchos más.
El número e, al igual que el número π, es un número trascendente, es decir, que no puede ser obtenido directamente mediante la resolución de una ecuación algebraica. Por lo tanto, es un irracional y su valor exacto no puede ser expresado como un número finito de cifras decimales o con decimales periódicos.
Su valor aproximado (truncado) es
e ≈ 2,7182818284590452354...Contenido[ocultar] |
[editar] Historia
Las primeras referencias a la constante fueron publicadas en 1618 en la tabla en un apéndice de un trabajo sobre logaritmos de John Napier.[2] No obstante, esta tabla no contenía el valor de la constante, sino que era simplemente una lista de logaritmos naturales calculados a partir de ésta. Se asume que la tabla fue escrita por William Oughtred.
El "descubrimiento" de la constante está acreditado a Jacob Bernoulli, quien estudió un problema particular del llamado interés compuesto. Si se invierte una Unidad Monetaria (que abreviaremos en lo sucesivo como UM) con un interés del 100% anual y se pagan los intereses una vez al año, se obtendrán 2 UM. Si se pagan los intereses 2 veces al año, dividiendo el interés entre 2, la cantidad obtenida es 1 UM multiplicado por 1,5 dos veces, es decir 1 UM x 1,502 = 2,25 UM. Si dividimos el año en 4 períodos (trimestres), al igual que la tasa de interés, se obtienen 1 UM x 1,254 = 2,4414... En caso de pagos mensuales el monto asciende a 1 UM x 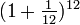 = 2,61303...UMs. Por tanto, cada vez que se aumenta la cantidad de períodos de pago en un factor de n (que tiende a crecer sin límite) y se reduce la tasa de interés en el período, en un factor de
= 2,61303...UMs. Por tanto, cada vez que se aumenta la cantidad de períodos de pago en un factor de n (que tiende a crecer sin límite) y se reduce la tasa de interés en el período, en un factor de 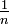 , el total de unidades monetarias obtenidas está expresado por la siguiente ecuación:
, el total de unidades monetarias obtenidas está expresado por la siguiente ecuación:
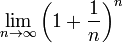
Bernoulli comprobó que esta expresión se aproxima al valor de 2,7182818...UMs. De aquí proviene la definición que se da de e en finanzas, que expresa que este número es el límite de una inversión de 1 UM con una tasa de interés al 100% anual compuesto en forma continua. En forma más general, una inversión que se inicia con un capital C y una tasa de interés anual R, proporcionará CeR UM con interés compuesto.
El primer uso conocido de la constante, representado por la letra b, fue en una carta de Gottfried Leibniz a Christiaan Huygens en 1690 y 1691. Leonhard Euler comenzó a utilizar la letra e para identificar la constante en 1727, y el primer uso de e en una publicación fue en Mechanica, de Euler, publicado en 1736. Mientras que en los años subsiguientes algunos investigadores usaron la letra c, e fue la más común, y finalmente se convirtió en la terminología usual.
[editar] Definición
La definición más común de e es como el valor límite de la serie
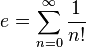
que se expande como
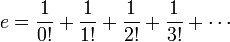
Otra definición habitual[3] dada a través del cálculo integral es como solución de la ecuación:
ln(x) = 1que implica
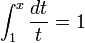
es decir que se define e como el número para el que
ln(e) = 1o lo que es lo mismo, el número para el que
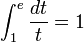
[editar] Propiedades
[editar] Cálculo
La función exponencial f(x) = ex es importante, en parte debido a que es la única función que es su propia derivada y vale 1 para x=0., y por lo tanto su propia primitiva también:
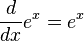
y
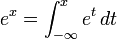
Además, e es el límite de la sucesión de término general:
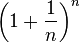
Primero, la propiedad se puede generalizar a una variable real, pasando del límite de una sucesión al de una función:
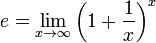
Como el término de la derecha tiene un exponente que varía, lo más práctico es tomar su logaritmo y hacer el cambio de variable h = 1 / x:
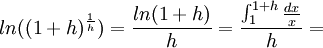
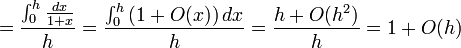
Como el logaritmo se aproxima a 1 cuando h tiende a cero por la derecha, la expresión original tiende hacia e.
[editar] Desarrollo decimal
El desarrollo decimal de e no muestra regularidad alguna. Sin embargo, con las fracciones continuas, que pueden ser normalizadas (con los numeradores todos iguales a 1) o no, obtenemos, en fracción continua normalizada:
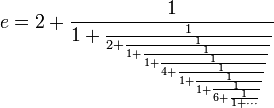
Lo que se escribe e = [2, 1,2,1, 1,4,1, 1,6,1 ... 1,2n,1, ... ], propiedad descubierta por Leonhard Euler, y en fracción continua no normalizada:
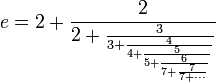
En ambos casos, e presenta regularidades no fortuitas.
[editar] Álgebra
El número real e es irracional, y también trascendental (ver Teorema de Lindemann–Weierstrass). Fue el primer número trascendental que fue probado como tal, sin haber sido construido específicamente para tal propósito (comparar con el número de Liouville). La demostración de esto fue dada por Charles Hermite en 1873. Se cree que e además es un número normal.
[editar] Números complejos
El número e presenta en la fórmula de Euler un papel importante relacionado con los números complejos:
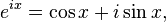
El caso especial con x = π es conocido como identidad de Euler
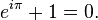
de lo que se deduce que:
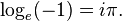
Además, utilizando las leyes de la exponenciación, se obtiene:
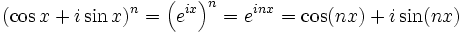
que es la fórmula de De Moivre.
[editar] Función exponencial
Se llama exponencial la función definida sobre los reales por 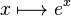
- La exponencial es la única función que es siempre igual a su derivada (de ahí su especial interés en el análisis, más precisamente para las ecuaciones diferenciales), y que toma el valor 1 cuando la variable vale 0.
- La exponencial se extiende al cuerpo de los complejos, mediante la relación:
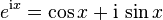 . Un caso particular de esta relación es la identidad de Euler.
. Un caso particular de esta relación es la identidad de Euler.
En 1975, el suizo Felix A. Keller descubrió la siguiente fórmula[4] que se aproxima a "e":
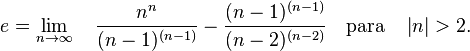
- Otro límite[5] con el que se obtiene el número e es:
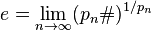
donde pn es el enésimo Número primo y 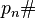 es el primorial del enésimo primo
es el primorial del enésimo primo
[editar] Representaciones de e
El número e puede ser representado como un número real en varias formas: como una serie infinita, un producto infinito, una fracción continua o como el límite de una sucesión. La principal de estas representaciones, particularmente en los cursos básicos de cálculo, es el límite:
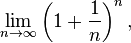
Desarrollando la potencia del binomio indicado en la propiedad anterior usando el teorema del binomio de Newton:
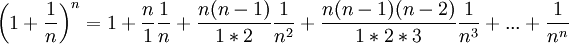
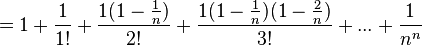
Cuando n tiende a infinito, los productos que están en los numeradores tienden a 1, por lo que cada término de esta expresión tiende a 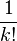 , como se quería demostrar.
, como se quería demostrar.
La serie infinita anterior no es única; e también puede ser representado como:
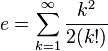
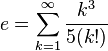
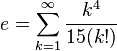
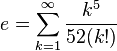
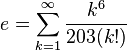
Existen otras representaciones menos comunes. Por ejemplo, e se puede representar como una fracción simple continua infinita:
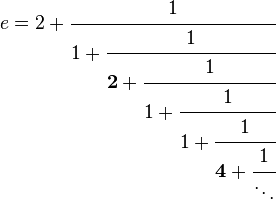
[editar] Dígitos conocidos
El número de dígitos conocidos de e ha aumentado enormemente durante las últimas décadas. Esto es debido tanto al aumento del desempeño de las computadoras como también a la mejora de los algoritmos utilizados.[6] [7]
| Fecha | Dígitos decimales | Cálculo realizado por |
|---|---|---|
| 1748 [8] | 18 | Leonhard Euler |
| 1853 | 137 | William Shanks |
| 1871 | 205 | William Shanks |
| 1884 | 346 | J. M. Boorman |
| 1946 | 808 | ? |
| 1949 | 2010 | John von Neumann (en la ENIAC) |
| 1961 | 100 265 | Daniel Shanks y John W. Wrench |
| 1994 | 10 000 000 | Robert Nemiroff y Jerry Bonnell |
| Mayo de 1997 | 18 199 978 | Patrick Demichel |
| Agosto de 1997 | 20 000 000 | Birger Seifert |
| Septiembre de 1997 | 50 000 817 | Patrick Demichel |
| Febrero de 1999 | 200 000 579 | Sebastian Wedeniwski |
| Octubre de 1999 | 869 894 101 | Sebastian Wedeniwski |
| 21 de noviembre de 1999 | 1 250 000 000 | Xavier Gourdon |
| 10 de julio de 2000 | 2 147 483 648 | Shigeru Kondo y Xavier Gourdon |
| 16 de julio de 2000 | 3 221 225 472 | Colin Martin y Xavier Gourdon |
| 2 de agosto de 2000 | 6 442 450 944 | Shigeru Kondo y Xavier Gourdon |
| 16 de agosto de 2000 | 12 884 901 000 | Shigeru Kondo y Xavier Gourdon |
| 21 de agosto de 2003 | 25 100 000 000 | Shigeru Kondo y Xavier Gourdon |
| 18 de septiembre de 2003 | 50 100 000 000 | Shigeru Kondo y Xavier Gourdon |
| 27 de abril de 2007 | 100 000 000 000 | Shigeru Kondo y Steve Pagliarulo |
| 6 de mayo de 2009 | 200 000 000 000 | Shigeru Kondo y Steve Pagliarulo |
[editar] Referencias
- ↑ Howard Whitley Eves (1969). An Introduction to the History of Mathematics. Holt, Rinehart & Winston. http://books.google.com/books?id=LIsuAAAAIAAJ&q=%22important+numbers+in+mathematics%22&dq=%22important+numbers+in+mathematics%22&pgis=1.
- ↑ O'Connor, John J.; Robertson, Edmund F. (2001), «The number e» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/HistTopics/e.html
- ↑ Esta forma de definir la función logaritmo natural, el número e, la función exponencial, etc. puede encontrarse en Cálculo Infinitesimal 2da edición, cap. 17 (p. 465) de Michael Spivak, Reverté o en Calculus 2da edición, cap. 6 (p. 277) de Tom Apostol, Reverté.
- ↑ Mathsoft "Expresión de Keller", Steven Finch (1998)
- ↑ Sebastián Martín Ruiz (1997)
- ↑ Sebah, P. and Gourdon, X.; The constant e and its computation
- ↑ Gourdon, X.; Reported large computations with PiFast
- ↑ New Scientist 21 de Julio de 2007 p.40
[editar] Véase también
[editar] Enlaces externos
- Un millón de cifras del número e.
- Fórmula para el cálculo de límites de sucesiones del tipo 1 elevado a infinito
0 comentarios