MATEMÁTICAS4: ¿ANTES DE LA POTENCIA? ¿PUDO HABER UNA RAÍZ? En matemática, las raíces n-ésimas de la unidad, o números de de Moivre, son todos los números complejos que resultan 1 cuando son elevados a una potencia dada n. Se puede demostrar que están localizados en el círculo unitario del plano complejo y que en ese plano forman los vértices de un polígono regular de n lados con un vértice sobre 1.
Raíz de la unidad
En matemática, las raíces n-ésimas de la unidad, o números de de Moivre, son todos los números complejos que resultan 1 cuando son elevados a una potencia dada n. Se puede demostrar que están localizados en el círculo unitario del plano complejo y que en ese plano forman los vértices de un polígono regular de n lados con un vértice sobre 1.
Contenido[ocultar] |
[editar] Definición
Los números complejos z solución a
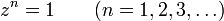
se denominan raíces n-ésimas de la unidad.
Hay n diferentes raíces n-ésimas de la unidad.
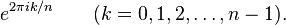
[editar] Raíces primitivas
Las raíces n-ésimas de la unidad forma con la multiplicación un grupo cíclico de orden n, y de hecho estos grupos comprenden todos los subgrupos finitos multiplicativos de los números complejos, excepto el grupo trivial {0}. Un generador de este grupo cíclico es una raíz primitiva n-ésima de la unidad. Las raíces primitivas n-ésimas de la unidad son e2πik / n, donde k y n son coprimos. El número de raíces primitivas diferentes lo da la función totiente de Euler, φ(n).
[editar] Ejemplos
Sólo hay una raíz primera de la unidad, igual a 1.
Las raíces segundas (raíces cuadradas) de la unidad son +1 y -1, siendo -1 la única primitiva.
Las raíces terceras (cúbicas) de la unidad son
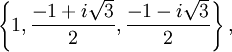
donde i es la unidad imaginaria; las dos últimas son primitivas.
Las raíces cuartas de la unidad son
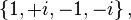
de las cuales + i y − i son primitivas.
Una de las raíces octavas primitivas de la unidad es
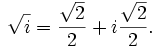
[editar] Sumatorio
Siempre que n sea al menos 2, las raíces n-ésimas de la unidad sumarán 0. Este hecho aparece en muchas áreas de la matemática y se puede probar de varias maneras. Una prueba elemental es aplicar la fórmula de la progresión geométrica:
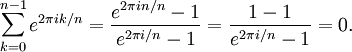
Otra razón de la suma nula es que las raíces de la unidad, dibujadas sobre el plano complejo, forman los vértices de un polígono regular cuyo baricentro (por simetría) está sobre el origen. Este sumatorio es un caso especial de la suma gaussiana.
[editar] Ortogonalidad
Se puede usar la fórmula del sumatorio para probar una relación de ortogonalidad:
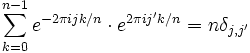
donde δ es la delta de Kronecker.
Las raíces n-ésimas de la unidad se pueden usar para formar una matriz 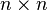 cuyo elemento Ai,j es
cuyo elemento Ai,j es
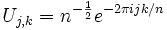
De lo anterior, las columnas de esta matriz son ortogonales y por tanto es unitaria. De hecho, esta matriz es precisamente la transformada de Fourier discreta (aunque varían la normalización y la convención de signos).
Las raíces n-ésimas de la unidad forman una representación irreducible de cualquier grupo cíclico de orden n. La relación de ortogonalidad se obtiene de los principios de teoría de grupos descritos en el grupo de caracteres.
Las raíces de la unidad aparecen en los autovectores de las matrices hermitianas (por ejemplo, de la laplaciana discretizada unidimensional con límites periódicos), de los que se obtiene también la propiedad de ortogonalidad (Stran, 1999).
[editar] Notación omega
La raíz primitiva e − 2πi / n (o su conjugada e2πi / n) se escribe a menudo ωn (o a veces simplemente ω), especialmente en el contexto de la transformada de Fourier discreta.
[editar] Polinomios ciclotómicos
Los ceros de un polinomio 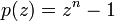 son precisamente las raíces n-ésimas de la unidad, cada una con multiplicidad 1.
son precisamente las raíces n-ésimas de la unidad, cada una con multiplicidad 1.
El polinomio ciclotómico n-ésimo está definido por el hecho de que sus ceros son precisamente las raíces primitivas n-ésimas de la unidad, cada una con multiplicidad 1: 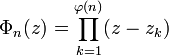 donde z1,...,zφ(n) son las raíces primitivas n-ésimas de la unidad, y φ(n) es la función totiente de Euler. El polinomio Φn(z) tiene coeficientes enteros y es un polinomio irreducible sobre los números racionales (es decir, no puede ser escrito como producto de dos polinomios de grado positivo con coeficientes racionales). El caso del primo n, que es más sencillo que la afirmación general, se obtiene del criterio de Eisenstein.
donde z1,...,zφ(n) son las raíces primitivas n-ésimas de la unidad, y φ(n) es la función totiente de Euler. El polinomio Φn(z) tiene coeficientes enteros y es un polinomio irreducible sobre los números racionales (es decir, no puede ser escrito como producto de dos polinomios de grado positivo con coeficientes racionales). El caso del primo n, que es más sencillo que la afirmación general, se obtiene del criterio de Eisenstein.
Cada raíz n-ésima de la unidad es una raíz primitiva d-ésima de la unidad para exactamente un divisor positivo d de n. Esto implica que
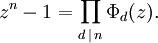
Esta fórmula representa la factorización del polinomio zn - 1 en factores irreducibles.
z1−1 = z−1z2−1 = (z−1)(z+1)z3−1 = (z−1)(z2+z+1)z4−1 = (z−1)(z+1)(z2+1)z5−1 = (z−1)(z4+z3+z2+z+1)z6−1 = (z−1)(z+1)(z2+z+1)(z2−z+1)z7−1 = (z−1)(z6+z5+z4+z3+z2+z+1)La aplicación de la inversión de Möbius a la fórmula nos da
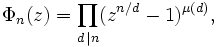
donde μ es la función de Möbius.
Así que los primeros polinomios ciclotómicos son
Φ1(z) = z−1Φ2(z) = (z2−1)(z−1)−1 = z+1Φ3(z) = (z3−1)(z−1)−1 = z2+z+1Φ4(z) = (z4−1)(z2−1)−1 = z2+1Φ5(z) = (z5−1)(z−1)−1 = z4+z3+z2+z+1Φ6(z) = (z6−1)(z3−1)−1(z2−1)−1(z−1) = z2−z+1Φ7(z) = (z7−1)(z−1)−1 = z6+z5+z4+z3+z2+z+1Si p es un número primo, entonces todas las raíces p-ésimas de la unidad excepto 1 son primitivas, y tenemos que
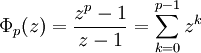
Observe que, al contrario de las apariencias, no todos los coeficientes de todos los polinomios ciclotómicos son 1, −1 o 0; el primer polinomio donde esto ocurre es Φ105, ya que 105=3×5×7 es el primer producto de tres primos impares. Se conocen muchas restricciones sobre los valores que pueden asumir los polinomios ciclotómicos con valores enteros. Por ejemplo, si p es primo y d | Φp(z) entonces 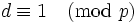 o
o 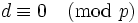 .
.
[editar] Cuerpos ciclotómicos
Adjuntando una raíz primitiva n-ésima de la unidad a Q, obtenemos el cuerpo ciclotómico n-ésimo Fn. Este cuerpo contiene todas las raíces n-ésimas de la unidad y es el cuerpo de descomposición de los polinomios ciclotómicos n-ésimos sobre Q. La extensión Fn/Q tiene grado φ(n) y su grupo de Galois es naturalmente isomorfo al grupo multiplicativo de las unidades del anillo Z/nZ.
Como el grupo de Galois de Fn/Q es abeliano, tenemos una extensión abeliana. Cada subcuerpo de uno ciclotómico es una extensión abeliana de los racionales. En estos casos la teoría de Galois se puede escribir en términos bastante explícitos de sumas gaussianas: esta teoría de las Disquisitiones Arithmeticae de Carl Friedrich Gauss se publicó muchos años antes de Galois.
A la inversa, cada extensión abeliana de los racionales es un subcuerpo de uno ciclotómico (éste es el contenido de un teorema de Kronecker, llamado normalmente teorema de Kronecker-Weber ya que Weber dio la demostración).
[editar] Referencias
- Lang, Serge (2002). Algebra, 3rd revised edition. Nueva York: Springer-Verlag. ISBN 0-387-95385-X.
- Milne, James S. (1998). «Algebraic Number Theory». Course Notes.
- Milne, James S. (1997). «Class Field Theory». Course Notes.
- Neukirch, Jürgen (1999). Algebraic Number Theory. Berlín: Springer-Verlag. ISBN 3-540-65399-6.
- Neukirch, Jürgen (1986). Class Field Theory. Berlín: Springer-Verlag. ISBN 3-540-15251-2.
- Washington, Lawrence C. (1997). Cyclotomic fields, 2nd edition. Nueva York: Springer-Verlag. ISBN 0-387-94762-0.
0 comentarios