MATEMÁTICAS: ¿CUÁLES SON LAS LEYES DE LA FORMA O LAS LEYES TRIGONOMÉTRICAS?. La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Se deriva del vocablo griego τριγωνο "triángulo" + μετρον "medida".
Trigonometría
Este artículo o sección necesita una revisión de ortografía y gramática (sugerencias para mejorar tu ortografía). Cuando se haya corregido, borra esta plantilla, por favor.
|
La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Se deriva del vocablo griego τριγωνο <trigōno> "triángulo" + μετρον <metron> "medida".[1]
La trigonometría es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos.
En términos generales, la trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

[editar] Unidades angulares
En la medida de ángulos, y por tanto en trigonometría, se emplean tres unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.
- Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes.
- Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
- Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.
[editar] Las funciones trigonométricas
La trigonometría como rama de las matemáticas realiza su estudio en la relación entre lados y ángulos de un triángulo rectángulo, con una aplicación inmediata en geometría y sus aplicaciones, para el desarrollo de este fin se definieron una serie de funciones, que han sobrepasado su fin original, convirtiendo en muchos casos en elementos matemáticos estudiados en sí mismos, y con aplicaciones en los campos más diversos.
[editar] Razones trigonométricas
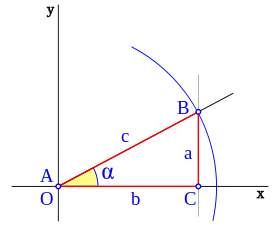
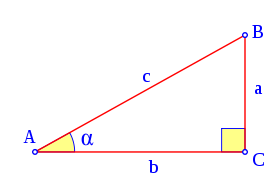
El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo 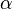 , correspondiente al vértice A, situado en el centro de la circunferencia.
, correspondiente al vértice A, situado en el centro de la circunferencia.
- El seno (abreviado como sen, o sin por llamarse "sinus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,
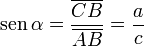
- El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
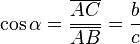
- La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,
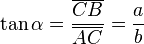
[editar] Razones trigonométricas recíprocas
- La Cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:
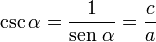
En el esquema su representación geométrica es:
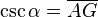
- La Secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:
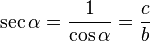
En el esquema su representación geométrica es:
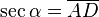
- La Cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:
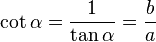
En el esquema su representación geométrica es:
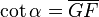
Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés especifico en hablar de ellos o las expresiones matemáticas se simplifiquen mucho, los términos cosecante, secante y cotangente no suelen utilizarse.
[editar] Otras funciones trigonométricas
Además de las funciones anteriores existen otras funciones trigonométricas, matemáticamente se pueden definir empleando las ya vistas, su uso no es muy corriente, pero si se emplean dado su sentido geométrico, veamos:
El seno cardinal o función sinc (x) definida:
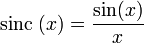
El verseno, es la distancia que hay entre la cuerda y el arco en una circunferencia, tambien se denomina sagita o flecha, se define:
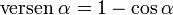
El semiverseno, se utiliza en navegación al intervenir en el calculo esférico:
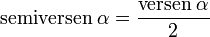
El coverseno,
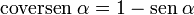
El semicoverseno
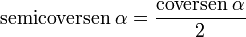
El exsecante:
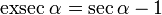
[editar] Funciones trigonométricas inversas
En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones inversas se denominan con el prefijo arco, así si:
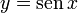
y es igual al seno de x, la función inversa:
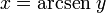
x es el arco cuyo seno vale y, o también x es el arcoseno de y.
si:
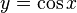
y es igual al coseno de x, la función inversa:
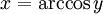
x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.
si:
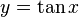
y es igual al tangente de x, la función inversa:
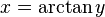
x es el arco cuya tangente vale y, ó x es igual al arcotangente de y.
[editar] Valor de las funciones trigonométricas
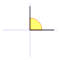
A continuación algunos valores de las funciones que es conveniente recordar:
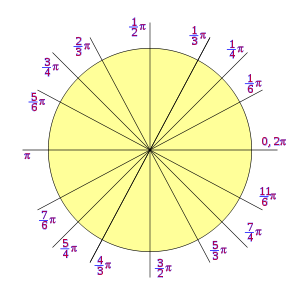 | 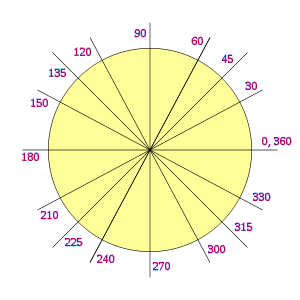 |
| Circunferencia en radianes. | Circunferencia en Grado sexagesimal. |
| Radianes | Grados sexag. | seno | coseno | tangente | cosecante | secante | cotangente | |
|---|---|---|---|---|---|---|---|---|
 | 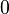 | 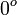 | 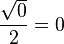 | 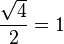 | 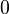 | 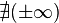 | 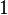 | 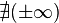 |
 | 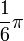 | 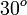 | 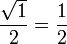 | 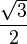 | 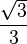 | 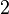 | 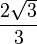 | 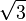 |
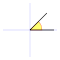 | 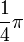 | 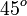 | 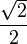 | 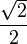 | 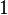 | 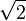 | 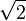 | 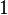 |
 | 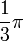 | 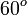 | 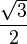 | 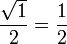 | 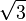 | 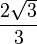 | 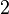 | 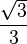 |
 | 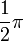 | 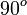 | 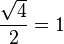 | 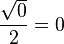 | 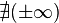 | 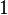 | 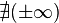 | 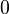 |
Para el calculo del valor de las funciones trigonométricas se confeccionaron tablas trigonométricas. La primera de estas tablas fue desarrollada por Johann Müller Regiomontano en 1467, que nos permiten, conocido un ángulo, calcular los valores de sus funciones trigonométricas. En la actualidad dado el desarrollo de la informática, en prácticamente todos los lenguajes de programación existen librerías de funciones que realizan estos cálculos, incorporadas incluso en calculadoras electrónicas de bolsillo, por lo que el empleo actual de las tablas resulta obsoleto.
[editar] Sentido de las funciones trigonométricas
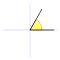
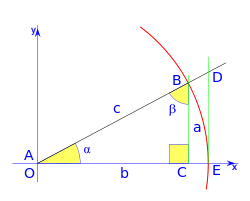
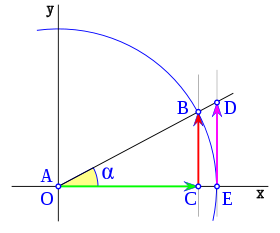
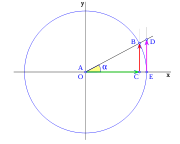
Dados los ejes de coordenadas cartesianas xy, de centro O, y una circunferencia goniométrica (circunferencia de radio la unidad) con centro en O; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto E.
Notese que el punto A es el vertice del triangulo, y O es el centro de coordenada del sistema de referencia:
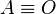
a todos los efectos.
La recta r, que pasa por O y forma un ángulo 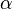 sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
Por semejanza de triángulos:
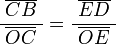
Los puntos E y B están en la circunferencia de centro O, por eso la distancia 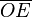 y
y 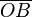 son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
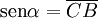
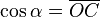
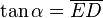
tenemos:
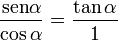
La tangente es la relación del seno entre el coseno, según la definición ya expuesta.
[editar] Primer cuadrante
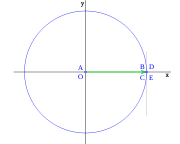
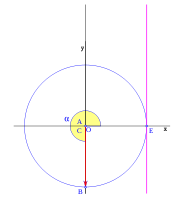
Para ver la evolución de las funciones trigonométricas según aumenta el ángulo, daremos una vuelta completa a la circunferencia, viéndolo por cuadrantes, los segmentos correspondientes a cada función trigonométrica variaran de longitud, siendo esta variación función del ángulo, partiendo en el primer cuadrante de un ángulo cero.
Partiendo de esta representación geométrica de las funciones trigonométricas, podemos ver las variaciones de las funciones a medida que aumenta el ángulo 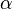 .
.
Para 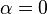 , tenemos que B, D, y C coinciden en E, por tanto:
, tenemos que B, D, y C coinciden en E, por tanto:
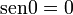
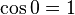
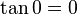
Si aumentamos progresivamente el valor de 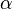 , las distancias
, las distancias 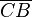 y
y 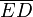 aumentarán progresivamente, mientras que
aumentarán progresivamente, mientras que 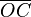 disminuirá.
disminuirá.
Percatarse que el punto B es de la circunferencia y cuando el ángulo aumenta se desplaza sobre ella.
El punto E es la intersección de la circunferencia con el eje x y no varia de posición.
Los segmentos: 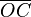 y
y 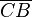 están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero
están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero 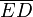 no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo
no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo 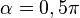 rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia
rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia 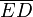 será infinita.
será infinita.
El punto C coincide con A y el coseno vale cero. El punto B esta en el eje y en el punto más alto de la circunferencia y el seno toma su mayor valor: uno.
Para un ángulo recto las funciones toman los valores:
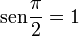
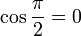
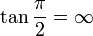
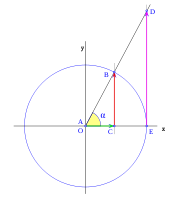
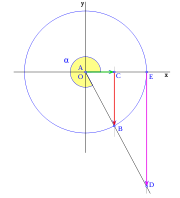
[editar] Segundo cuadrante
Cuando el ángulo 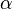 supera el ángulo recto, el valor del seno empieza a disminuir según el segmento
supera el ángulo recto, el valor del seno empieza a disminuir según el segmento 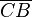 , el coseno aumenta según el segmento
, el coseno aumenta según el segmento 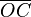 , pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
, pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
La tangente para un ángulo 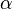 inferior a
inferior a 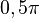 rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los
rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los 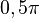 rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente
rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa por E en el punto D real, en el lado negativo de las y, la tangente 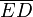 por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo
por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo 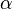 aumenta progresivamente hasta los
aumenta progresivamente hasta los 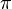 rad.
rad.
Resumiendo: en el segundo cuadrante el seno de 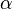 ,
, 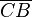 , disminuye progresivamente su valor desde 1, que toma para
, disminuye progresivamente su valor desde 1, que toma para 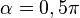 rad, hasta que valga 0, para
rad, hasta que valga 0, para  rad, el coseno,
rad, el coseno,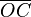 , toma valor negativo y su valor varia desde 0 para
, toma valor negativo y su valor varia desde 0 para 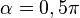 rad, hasta –1, para
rad, hasta –1, para  rad.
rad.
La tangente conserva la relación:
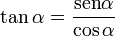
incluyendo el signo de estos valores.
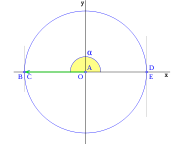
Para un ángulo llano tenemos que el punto D esta en E, y B y C coinciden en el eje de las x en el lado opuesto de E, con lo que tenemos:
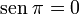
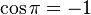
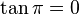
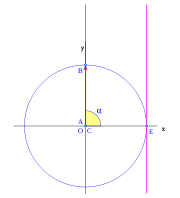
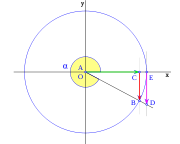
[editar] Tercer cuadrante
En el tercer cuadrante, comprendido entre los valores del ángulo  rad a
rad a 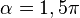 rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para
rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para 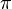 rad:
rad:
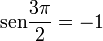
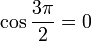
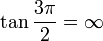
Cuando el ángulo 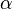 aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
A medida que el ángulo crece el punto C se acerca a O, y el segmento 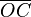 , el coseno, se hace más pequeño en el lado negativo de las x.
, el coseno, se hace más pequeño en el lado negativo de las x.
El punto B, intersección de la circunferencia y la vertical que pasa por C, se aleja del eje de las x, en el sentido negativo de las y, el seno, 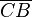 .
.
Y el punto D, intersección de la prolongación de la recta r y la vertical que pasa por E, se aleja del eje las x en el sentido positivo de las y, con lo que la tangente, 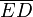 , aumenta igual que en el primer cuadrante
, aumenta igual que en el primer cuadrante
Cuando el ángulo 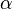 alcance
alcance 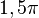 rad, el punto C coincide con O y el coseno valdrá cero, el segmento
rad, el punto C coincide con O y el coseno valdrá cero, el segmento 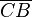 será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
El seno el coseno y la tangente siguen conservando la misma relación:
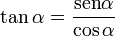
que se cumple tanto en valor como en signo, nótese que cuando el coseno vale cero, la tangente se hace infinito.
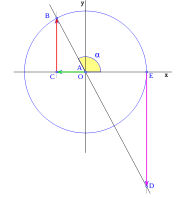
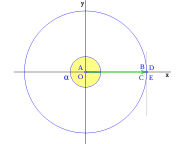
[editar] Cuarto cuadrante
En el cuarto cuadrante, que comprende los valores del ángulo 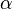 entre
entre 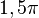 rad y
rad y 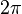 rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para 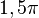 rad:
rad:
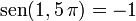
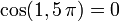

hasta los que toman para 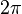 rad pasando al primer cuadrante, completando una rotación:
rad pasando al primer cuadrante, completando una rotación:
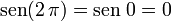
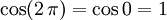
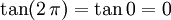
como puede verse a medida que el ángulo 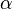 aumenta, aumenta el coseno
aumenta, aumenta el coseno 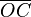 en el lado positivo de las x, el seno
en el lado positivo de las x, el seno 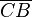 disminuye en el lado negativo de las y, y la tangente
disminuye en el lado negativo de las y, y la tangente 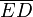 también disminuye en el lado negativo de las y.
también disminuye en el lado negativo de las y.
Cuando 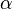 , vale
, vale 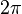 ó
ó 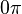 al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
Dado el carácter rotativo de las funciones trigonométricas, se puede afirmar en todos los casos:
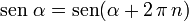
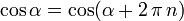
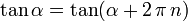
Que cualquier función trigonométrica toma el mismo valor si se incrementa el ángulo un número entero de rotaciones completas.
[editar] Representación gráfica

[editar] Calculo de algunos casos
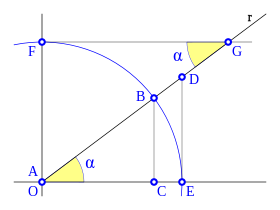
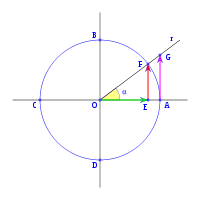
Partiendo de una circunferencia de radio uno, dividida en cuatro cuadrantes, por dos rectas perpendiculares, que se cortan en el centro de la circunferencia O, estas rectas cortan a la circunferencia en los puntos A, B, C y D, la recta horizonte AC también la podemos llamar eje x y la recta vertical BD eje y. Dada una recta r, que pasa por el centro de la circunferencia y forma un ángulo α con OA, eje x, y corta a la circunferencia en F, tenemos que la vertical que pasa por F corta al eje x en E, la vertical que pasa por A corta a la recta r en G. Con todo esto definimos, como ya se vio anteriormente, las funciones trigonométricas:
para el seno:
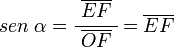
dado que:
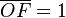
Para el coseno:
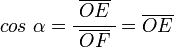
dado que:
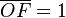
Para la tangente:
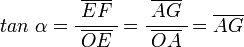
dado que:
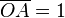
partiendo de estas definiciones, podemos ver algunos caso importantes:
[editar] Para 90-α
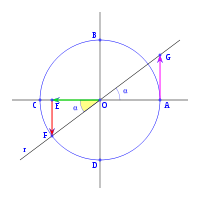
Si a partir del eje vertical OB trazamos la recta r a un ángulo α en el sentido horario, la recta r forma con el eje x un ángulo 90-α, el valor de las funciones trigonométricas de este ángulo conocidas las de α serán:
El triángulo OEF rectángulo en E, siendo el ángulo en F α, por lo tanto:
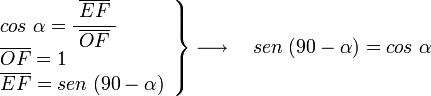
en el mismo triángulo OEF, tenemos que:
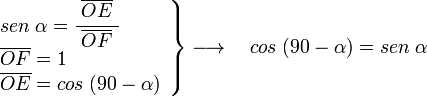
viendo el triángulo OAG, rectángulo en A, siendo el ángulo en G igual a α, podemos ver:
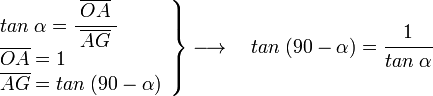
[editar] Para 90+α
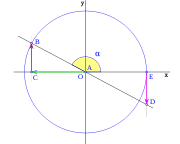
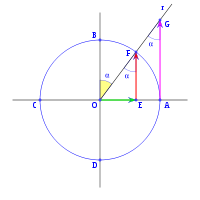
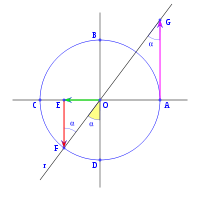
Si a partir de eje vertical OB trazamos la recta r a un ángulo α, medido en sentido trigonométrico, el ángulo formado por el eje horizontal OA y la recta r será 90+α. La prolongación de la recta r corta a la circunferencia en F y a la vertical que pasa por A en G.
El triángulo OEF es rectángulo en E y su ángulo en F es α, por lo tanto tenemos que:
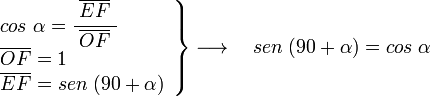
En el mismo triángulo OEF podemos ver:
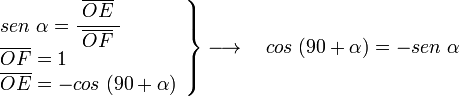
En el triángulos OAG rectángulo A y siendo α el ángulo en G, tenemos:
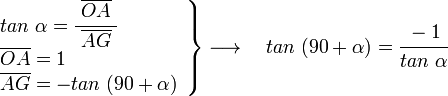
[editar] Para 180-α
Si sobre el eje horizontal OC, trazamos la recta r a un ángulo α, el ángulo entre el eje OA y la recta r es de 180-α, dado el triángulo OEF rectángulo en E y cuyo ángulo en O es α, tenemos:
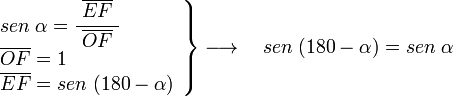
en el mismo triángulo OEF:
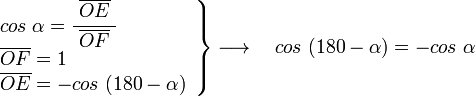
En el triángulo OAG, rectángulo en A y con ángulo en O igual a α, tenemos:
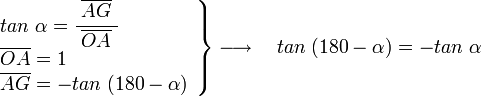
[editar] Para 180+α
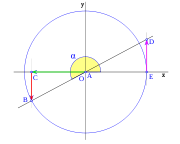
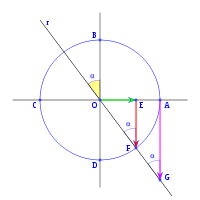
Sobre la circunferencia de radio uno, a partir del eje OC con un ángulo α trazados la recta r, el ángulo del eje OA y la recta r es de 180+α, como se ve en la figura. En el triángulo OEF rectángulo en E se puede deducir:

en el mismo triángulo OEF tenemos:
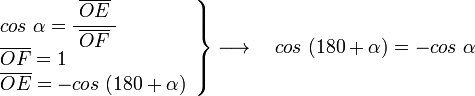
en el triángulo OAG, rectángulo en A, vemos que:
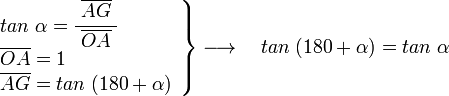
[editar] Para 270-α
Sobre el eje OD y con un ángulo α medido en sentido horario trazamos la recta r. El ángulo entre el eje OA y la recta r es de 270-α. En el triángulo OEF, rectángulo en E, tenemos:
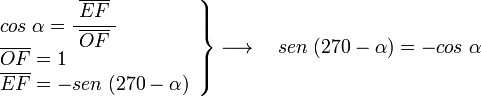
por otra parte en el mismo triángulo OEF, tenemos:
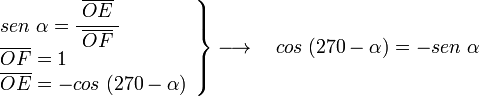
en el triángulo OAG rectángulo en A, y siendo α el ángulo en G, tenemos;
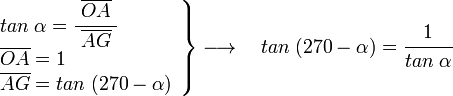
[editar] Para 270+α
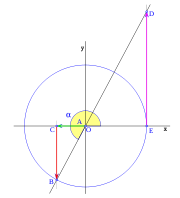
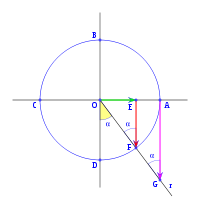
Sobre el eje OD y con un ángulo α medido en sentido trigonometrico, trazamos la recta r. El ángulo entre el eje OA y la recta r es de 270+α. En el triángulo OEF, rectángulo en E, tenemos:
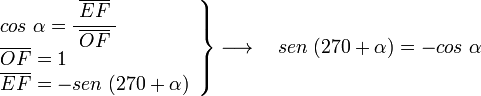
por otra parte en el mismo triángulo OEF, tenemos:
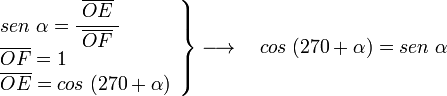
en el triángulo OAG rectángulo en A, y siendo α el ángulo en G, tenemos;
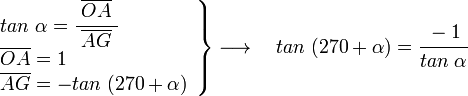
[editar] Para -α
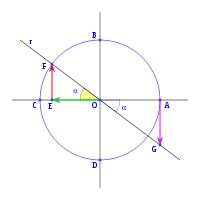
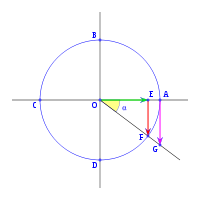
Sobre la circunferencia de radio uno, a partir del eje OA con un ángulo α medido en sentido horario trazados la recta r, el ángulo del eje OA y la recta r es de -α, o lo que es lo mismo 360-α como se ve en la figura. En el triángulo OEF rectángulo en E se puede deducir:
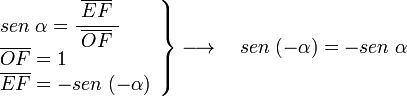
en el mismo triángulo OEF tenemos:
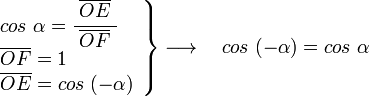
en el triángulo OAG, rectángulo en A, vemos que:
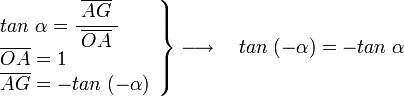
[editar] Identidades trigonométricas
Una identidad es una igualdad en que se cumple para todos los valores permisibles de la variable. En trigonometría existen seis identidades fundamentales:
[editar] Recíprocas
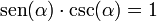
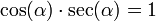
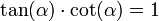
[editar] De división
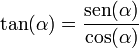
[editar] Por el teorema de Pitágoras
Como en el triángulo rectángulo cumple la funcion que:
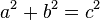
de la figura anterior se tiene que:
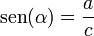
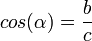
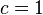
entonces para todo ángulo α, se cumple la identidad Pitagórica :
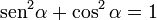
que también puede expresarse:
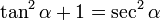
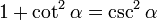
[editar] Suma y diferencia de dos ángulos
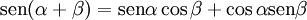
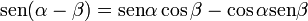
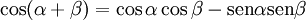
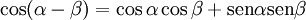
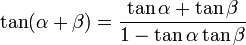
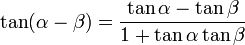
[editar] Suma y diferencia del seno y coseno de dos ángulos
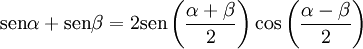
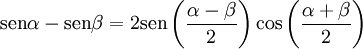
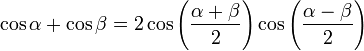

[editar] Producto del seno y coseno de dos ángulos
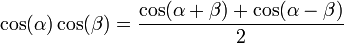
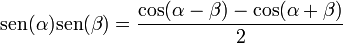
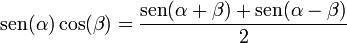
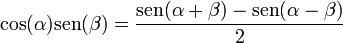
[editar] Ángulo doble
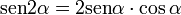
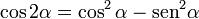
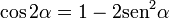
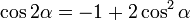
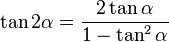
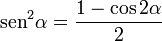
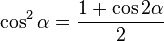
[editar] Ángulo mitad
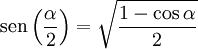
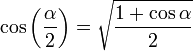
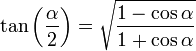
[editar] Otras identidades trigonométricas
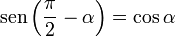
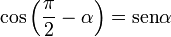
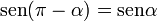
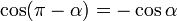
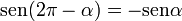
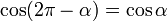
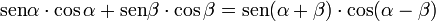
[editar] Seno y coseno, funciones complejas
El seno y coseno se definen en matemática compleja, gracias a la fórmula de Euler como:
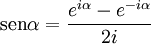
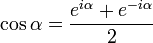
Por lo tanto, la tangente quedará definida como:
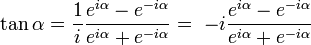
Siendo 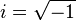 (también puede representarse como j).
(también puede representarse como j).
[editar] Referencias
- ↑ «Etimología de la palabra "trigonometría"». Diccionario web de etimología (inglés).
[editar] Bibliografía
- Cortés Espinosa de los Monteros, Nuria. Ediciones Didácticas y Pedagógicas S. L.. ed. Actividades para unidad didáctica sobre trigonometría [Recurso electrónico] (2008). ISBN 978-84-936336-3-9.
- Domínguez Muro, Mariano. Universidad de Salamanca. Ediciones Universidad Salamanca. ed. Trigonometría activa: 2 BUP (1985). ISBN 978-84-7800-056-2.
[editar] Véase también
- Historia de la trigonometría
- Función trigonométrica
- Identidad trigonométrica
- Funciones hiperbólicas
- Lista de integrales de funciones trigonométricas
- Fórmula de Euler y Número complejo, para funciones trigonométricas complejas
- Trigonometría esférica
[editar] Enlaces externos
 Wikilibros alberga un libro o manual sobre Tabla trigonométrica.
Wikilibros alberga un libro o manual sobre Tabla trigonométrica.- Ejercicios de Trigonometría (Proyecto Descartes para Educación Secundaria del Ministerio de Educación de España).
- Álgebra y Trigonometría. Universidad de Chile
- Trigonometría (Applets con Geogebra de Manuel Sada).
- Trigonometría. Precálculo21
- Orígenes de la trigonometría (Webquest).
- Matemática - Trigonometría (Apuntes y ejercicios de Trigonometría en Fisicanet).
- Unidad Didáctica. Razones Trigonométricas (IES López de Arenas, de Marchena (Sevilla)).
- La trigonometría, ¿para qué sirve?
- Funciones trigonométricas (Proyecto Descartes para Educación Secundaria del Ministerio de Educación de España).

1 comentario
petalofucsia -