MATEMÁTICAS: EL NÚMERO AUREO. El número áureo o de oro (también llamado número plateado, razón extrema y media,[1] razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en minúscula) o Φ (fi) (en mayúscula), en honor al escultor griego Fidias, es un número irracional.
Número áureo
El número áureo o de oro (también llamado número plateado, razón extrema y media,[1] razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en minúscula) o Φ (fi) (en mayúscula), en honor al escultor griego Fidias, es un número irracional:[2]
También se representa con la letra griega Tau (Τ τ),[3] por ser la primera letra de la raíz griega τομή, que significa acortar, aunque encontrarlo representado con la letra Fi (Φ,φ) es más común.
Se trata de un número algebraico irracional (decimal infinito no periódico) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre segmentos de rectas. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.
Asimismo, se atribuye un carácter estético especial a los objetos que siguen la razón áurea, así como una importancia mística. A lo largo de la historia, se le ha atribuido importancia en diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido objetables para las matemáticas y la arqueología.
[editar] Definición
| Números γ - ζ(3) - √2 - √3 - √5 - φ - α - e - π - δ | |
| Binario | 1,1001111000110111011... |
| Decimal | 1,6180339887498948482... |
| Hexadecimal | 1,9E3779B97F4A7C15F39... |
| Fracción continua | 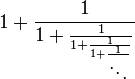 |
| Algebraico | 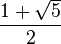 |
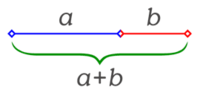
Se dice que dos números positivos a y b están en razón áurea si y sólo si:
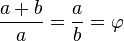
Para obtener el valor de 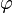 a partir de esta razón considere lo siguiente:
a partir de esta razón considere lo siguiente:
Que la longitud del segmento más corto b sea 1 y que la de a sea x. Para que estos segmentos cumplan con la razón áurea deben cumplir que:
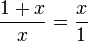
Multiplicando ambos lados por x y reordenando:
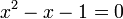
Mediante la fórmula general de las ecuaciones de segundo grado se obtiene que las dos soluciones de la ecuación son
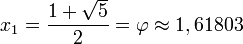
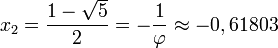
La solución positiva es el valor del número áureo.
[editar] Historia del número áureo
Existen varios textos que sugieren que el número áureo se encuentra como proporción en ciertas estelas Babilonias y Asirias de alrededor de 2000 a. C. Sin embargo, no existe documentación histórica que indique que el número áureo fue usado conscientemente por los arquitectos o artistas en la construcción de las estelas. También es importante notar que cuando se mide una estructura complicada es fácil obtener resultados curiosos si se tienen muchas medidas disponibles. Además para que se pueda considerar que el número áureo está presente, las medidas deben tomarse desde puntos relativamente obvios del objeto y este no es el caso de los elaborados teoremas que defienden la presencia del número áureo. Por todas estas razones Mario Livio y Álvaro Valarezo concluyen que es muy improbable que los babilonios hayan descubierto el número áureo.[4]
El primero en hacer un estudio formal sobre el número áureo fue Euclides (c. 300-265 a. C.), quién lo definió de la siguiente manera:
Euclides demostró también que este número no puede ser descrito como la razón de dos números enteros, es decir es irracional.
Platón (c. 428-347 a. C.) vivió antes de que Euclides estudiara el número áureo, sin embargo, a veces se le atribuye el desarrollo de teoremas relacionados con el número áureo debido que el historiador griego Proclo escribió:
Aquí a menudo se interpretó la palabra sección (τομή) como la sección áurea. Sin embargo a partir del siglo XIX esta interpretación ha sido motivo de gran controversia y muchos investigadores han llegado a la conclusión de que la palabra sección no tuvo nada que ver con el número áureo. No obstante, Platón consideró que los números irracionales, descubiertos por los pitagóricos, eran de particular importancia y la llave a la física del cosmos. Esta opinión tuvo una gran influencia en muchos filósofos y matemáticos posteriores, en particular los neoplatónicos.
A pesar de lo discutible de su conocimiento sobre el número áureo, Platón se dio a la tarea de estudiar el origen y la estructura del cosmos, cosa que intentó usando los cinco sólidos platónicos, construidos y estudiados por Teeteto. En particular, combinó la idea de Empédocles sobre la existencia de cuatro elementos básicos de la materia, con la teoría atómica de Demócrito. Para Platón cada uno de los sólidos correspondía a una de las partículas que conformaban cada uno de los elementos: la tierra estaba asociada al cubo, el fuego al tetraedro, el aire al octaedro, el agua al icosaedro, y finalmente el Universo como un todo, estaba asociado con el dodecaedro.
En 1509 el matemático y teólogo Luca Pacioli publica su libro De Divina Proportione (La Proporción Divina), en el que plantea cinco razones por las que considera apropiado considerar divino al Número áureo:
- La unicidad; Pacioli compara el valor único del número áureo con la unicidad de Dios.
- El hecho de que esté definido por tres segmentos de recta, Pacioli lo asocia con la Trinidad.
- La inconmensurabilidad; para Pacioli la inconmensurabilidad del número áureo, y la inconmensurabilidad de Dios son equivalentes.
- La Autosimilaridad asociada al número áureo; Pacioli la compara con la omnipresencia e invariabilidad de Dios.
- Según Pacioli, de la misma manera en que Dios dio ser al Universo a través de la quinta esencia, representada por el dodecaedro; el número áureo dio ser al dodecaedro.
En 1525, Alberto Durero publica Instrucción sobre la medida con regla y compás de figuras planas y sólidas donde describe cómo trazar con regla y compás la espiral basada en la sección áurea, que se conoce como “espiral de Durero”.
El astrónomo Johannes Kepler (1571-1630), desarrolló un modelo Platónico del Sistema Solar utilizando los sólidos platónicos, y se refirió al número áureo en términos grandiosos
El primer uso conocido del adjetivo áureo, dorado, o de oro, para referirse a este número lo hace el matemático alemán Martin Ohm, hermano del célebre físico Georg Simon Ohm, en la segunda edición de 1835 de su libro Die Reine Elementar Matematik (Las Matemáticas Puras Elementales). Ohm escribe en una nota al pie:
A pesar de que la forma de escribir sugiere que el término ya era de uso común para la fecha, el hecho de que no lo incluyera en su primera edición sugiere que el término pudo ganar popularidad alrededor de 1830.
En los textos de matemáticas que trataban el tema, el símbolo habitual para representar el número áureo fue τ del griego τομή que significa corte o sección. Sin embargo, la moderna denominación Φ ó φ, la efectuó en 1900 el matemático Mark Barr en honor a Fidias ya que ésta era la primera letra de su nombre escrito en griego (Φειδίας). Este honor se le concedió a Fidias por el máximo valor estético atribuido a sus esculturas, propiedad que ya por entonces se le atribuía también al número áureo. Mark Barr y Schooling fueron responsables de los apéndices matemáticos del libro The Curves of Live, de Sir Theodore Cook.
[editar] El número áureo en las Matemáticas
[editar] Fórmula de la relación Áurea
Para conseguir un número cuya relación con otro sea φ se puede utilizar esta fórmula:
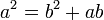
Siendo siempre a>b, a>0 y b>0
Si por ejemplo, queremos un valor áureo para 2 siendo éste el segmento menor, o sea b, resulta que:
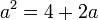
Ordenando:
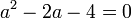
Con la fórmula Cuadrática:
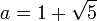
[editar] Propiedades y representaciones
[editar] Ángulo de oro
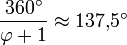
[editar] Propiedades algebraicas
- Φ es el único número real positivo tal que:
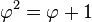
La expresión anterior es fácil de comprobar:
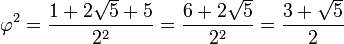
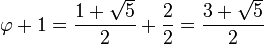
- Φ posee además las siguientes propiedades:
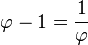
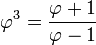
- Las potencias del número áureo pueden ser escritas en función de una suma de potencias de grados inferiores del mismo número, estableciendo una verdadera sucesión recurrente de potencias.
El caso más simple es: Φn = Φn − 1 + Φn − 2, cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores.
Una ecuación recurrente de orden k tiene la forma a1un + k − 1 + a2un + k − 2 + ... + akun, donde ai es cualquier número real o complejo y k es un número natural menor o igual a n y mayor o igual a 1. En el caso anterior es k = 2, a1 = 1 y a2 = 1.
Pero podemos «saltear» la potencia inmediatamente anterior y escribir:
Φn = Φn − 2 + 2Φn − 3 + Φn − 4. Aquí k = 4, a1 = 0, a2 = 1, a3 = 2 y a4 = 1.
Si anulamos a las dos potencias inmediatamente anteriores, también hay una fórmula recurrente de orden 6:
Φn = Φn − 3 + 3Φn − 4 + 3Φn − 5 + Φn − 6
En general:
![Phi^n = sum_{i=0}^{textstyle frac {1}{2} k}{textstyle frac{1}{2}kchoose i}Phi^{left [textstyle n-left(textstyle frac{1}{2}k+iright)right]}textstyle;k=2jin mathbb{N},textstyle, nin mathbb{N},textstyle, iin mathbb{N}](https://petalofucsia.blogia.com/upload/externo-1eaef1f12faa542d241d55f5264cbd63.png) .
.
En resumen: cualquier potencia del número áureo puede ser considerada como el elemento de una sucesión recurrente de órdenes 2, 4, 6, 8, ..., 2k; donde k es un número natural. En la fórmula recurrente es posible que aparezcan potencias negativas de Φ, hecho totalmente correcto. Además, una potencia negativa de Φ corresponde a una potencia positiva de su inverso, la sección áurea.
Este curioso conjunto de propiedades y el hecho de que los coeficientes significativos sean los del binomio, parecieran indicar que entre el número áureo y el número e hay un parentesco.
- El número áureo
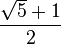 es la unidad fundamental «ε» del cuerpo
es la unidad fundamental «ε» del cuerpo 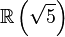 y la sección áurea
y la sección áurea 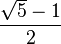 es su inversa, «
es su inversa, «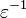 ». En esta extensión el «emblemático» número irracional
». En esta extensión el «emblemático» número irracional 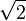 cumple las siguientes igualdades:
cumple las siguientes igualdades:
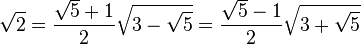 .
.
[editar] Representación mediante fracciones continuas
La expresión mediante fracciones continuas es:
Esta iteración es la única donde sumar es multiplicar y restar es dividir. Es también la más simple de todas las fracciones continuas y la que tiene la convergencia más lenta. Esa propiedad hace que además el número áureo sea un número mal aproximable mediante racionales que de hecho alcanza el peor grado de aproximabilidad mediante racionales posible.[5]
Por ello se dice que φ es el número más alejado de lo reacional o el número más irracional. Este es el motivo por el cual aparece en el teorema de Kolmogórov-Arnold-Moser.
[editar] Representación mediante ecuaciones algebraicas
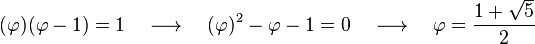
El número áureo 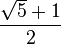 y la sección áurea
y la sección áurea 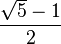 son soluciones de las siguientes ecuaciones:
son soluciones de las siguientes ecuaciones:
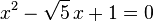
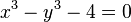
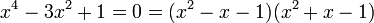
[editar] Representación trigonométrica
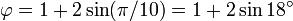
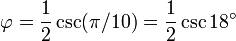
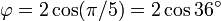
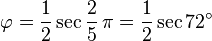
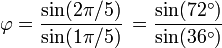
Éstas corresponden al hecho de que el diámetro de un pentágono regular (distancia entre dos vértices no consecutivos) es φ veces la longitud de su lado, y de otras relaciones similares en el pentagrama.
En 1994 se derivaron las siguientes ecuaciones relacionando al número áureo con el número de la Bestia:
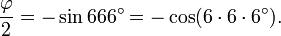
Lo que puede combinarse en la expresión:
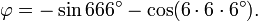
Sin embargo, hay que notar que estas ecuaciones dependen de que se elijan los grados sexagesimales como unidad angular, ya que las ecuaciones no se mantienen para unidades diferentes.
[editar] Representación mediante raíces anidadas
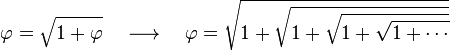
Esta fórmula como caso particular de una identidad general publicada por Nathan Altshiller-Court, de la Universidad de Oklahoma, en la revista American Mathematical Monthly, 1917.
El teorema general dice:
La expresión 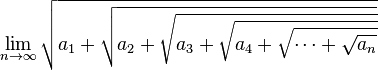 (donde ai = a), es igual a la mayor de las raíces de la ecuación x² - x - a = 0; o sea,
(donde ai = a), es igual a la mayor de las raíces de la ecuación x² - x - a = 0; o sea, 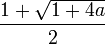
[editar] Relación con la serie de Fibonacci
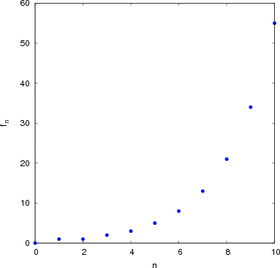
Si se denota el enésimo número de Fibonacci como Fn, y al siguiente número de Fibonacci, como Fn + 1, descubrimos que a medida que n aumenta, esta razón oscila siendo alternativamente menor y mayor que la razón áurea. Podemos también notar que la fracción continua que describe al número áureo produce siempre números de Fibonacci a medida que aumenta el número de unos en la fracción. Por ejemplo: 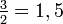 ;
; 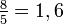 ; y
; y 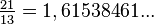 , lo que se acerca considerablemente al número áureo. Entonces se tiene que:
, lo que se acerca considerablemente al número áureo. Entonces se tiene que:
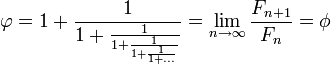
Esta propiedad fue descubierta por el astrónomo alemán Johannes Kepler, sin embargo, pasaron más de cien años antes de que fuera demostrada por el matemático inglés Robert Simson.
Con posterioridad se encontró que cualquier sucesión aditiva recurrente de orden 2 tiende al mismo límite. Por ejemplo, si tomamos dos números naturales arbitrarios, como pudieran ser 3 y 7, la sucesión recurrente resulta: 3 - 7 - 10 - 17 - 27 - 44 - 71 - 115 - 186 - 301 ... Los cocientes de términos sucesivos producen aproximaciones racionales que se acercan asintóticamente por exceso y por defecto al mismo límite: 44/27 = 1,6296296...; 71/44 = 1,613636...; 301/186 = 1,6182795... [6]
A mediados del siglo XIX el matemático francés Jacques Philippe Marie Binet redescubrió una fórmula que aparentemente ya era conocida por Leonhard Euler, y por otro matemático francés, Abraham de Moivre. La fórmula permite encontrar el enésimo número de Fibonacci sin la necesidad de producir todos los números anteriores. La fórmula de Binet depende exclusivamente del número áureo:
![F_n = frac{1}{sqrt{5}} left [ left (frac{1 +sqrt{5}}{2} right )^n - left (frac{1 - sqrt{5}}{2}right )^n right ]quad=frac{1}{sqrt{5}} left [ left ( phi right )^n - left (frac{-1}{phi} right )^n right ] quad](https://petalofucsia.blogia.com/upload/externo-acd42fa99ff8946ab1fe9fc9246b0c9d.png)
[editar] El número áureo en la geometría
El número áureo y la sección áurea están presentes en todos los objetos geométricos regulares o semiregulares en los que haya simetría pentagonal, pentágonos o aparezca de alguna manera la raíz cuadrada de cinco.
- Relaciones entre las partes del pentágono.
- Relaciones entre las partes del pentágono estrellado, pentáculo o pentagrama.
- Relaciones entre las partes del decágono.
- Relaciones entre las partes del dodecaedro y del icosaedro.
[editar] El rectángulo áureo de Euclides
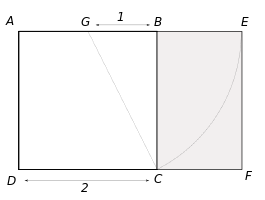
El rectángulo AEFD es áureo porque sus lados AE y AD están en la proporción del número áureo. Euclides en su proposición 2.11 de Los elementos obtiene su construcción.>
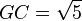
Con centro en G se obtiene el punto E, y por lo tanto
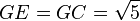
resultando evidente que
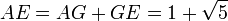
de donde, finalmente
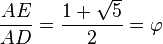
Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que este último es asimismo un rectángulo áureo.
[editar] En el pentagrama
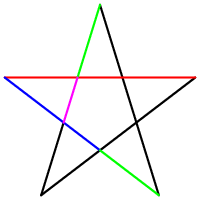
El número áureo tiene un papel muy importante en los pentágonos regulares y en los pentagramas. Cada intersección de partes de un segmento, interseca a otro segmento en una razón áurea.
El pentagrama incluye diez triángulos isóceles: cinco acutángulos y cinco obtusángulos. En ambos, la razón de lado mayor y el menor es φ. Estos triángulos se conocen como los triángulos áureos.
Teniendo en cuenta la gran simetría de este símbolo se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande. Al medir la longitud total de una de las cinco líneas del pentáculo interior, resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea Φ. Por lo tanto el número de veces en que aparece el número áureo en el pentagrama es infinito al anidar infinitos pentagramas.
[editar] El teorema de Ptolomeo y el pentágono

Claudio Ptolomeo desarrolló un teorema conocido como el teorema de Ptolomeo, el cual permite trazar un pentágono regular mediante regla y compás. Aplicando este teorema un cuadrilátero es formado al quitar uno de los vértices del pentágono, Si las diagonales y la base mayor miden b, y los lados y la base menor miden a, resulta que b2 = a2 + ab lo que implica:
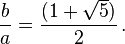
[editar] Relación con los sólidos platónicos
El número áureo está relacionado con los sólidos platónicos, en particular con el icosaedro y el dodecaedro, cuyas dimensiones están dadas en términos del número áureo. Los 12 vértices de un icosaedro con aristas de longitud 2, pueden darse en coordenadas cartesianas por los siguientes puntos: (0, ±1, ±φ), (±1, ±φ, 0), (±φ, 0, ±1)
Los 20 vértices de un dodecaedro con aristas de longitud 2/φ=√5−1, también se pueden dar en términos similares: (±1, ±1, ±1), (0, ±1/φ, ±φ), (±1/φ, ±φ, 0), (±φ, 0, ±1/φ)
Para un dodecaedro con aristas de longitud a, su volumen y su área total se pueden expresar también en términos del número áureo:
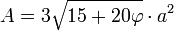
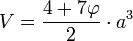
Si tres rectángulos áureos se solapan paralelamente en sus centros, las 12 esquinas de los rectángulos áureos coinciden exactamente con los vértices de un icosaedro, y con los centros de las caras de un dodecaedro:
El punto que los rectángulos tienen en común es el centro tanto del dodecaedro como del icosaedro.
[editar] El número áureo en la Naturaleza
| Existen desacuerdos sobre la neutralidad en el punto de vista de la versión actual de este artículo o sección. En la página de discusión puedes consultar el debate al respecto. |
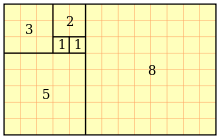
En la naturaleza, hay muchos elementos relacionados con la sección áurea y/o los números de Fibonacci:
- Leonardo de Pisa (Fibonacci), en su Libro de los ábacos (Liber abacci, 1202, 1228), usa la sucesión que lleva su nombre para calcular el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos están aislados por muros, se empiezan a reproducir cuando tienen dos meses de edad, tardan un mes desde la fecundación hasta la aparición y cada camada es de dos conejos). Este es un problema matemático puramente independiente de que sean conejos los involucrados. En realidad, el conejo común europeo tiene camadas de 4 a 12 individuos y varias veces al año, aunque no cada mes, pese a que la preñez dura 32 días. El problema se halla en las páginas 123 y 124 del manuscrito de 1228, que fue el que llegó hasta nosotros, y parece que el planteo recurrió a conejos como pudiera haber sido a otros seres; es un soporte para hacer comprensible una incógnita, un acertijo matemático . El cociente de dos términos sucesivos de la Sucesión de Fibonacci tiende a la sección áurea o al número áureo si la fracción resultante es propia o impropia, respectivamente. Lo mismo sucede con toda sucesión recurrente de orden dos, según demostraron Barr y Schooling en la revista The Field del 14 de diciembre de 1912.[7]
- La relación entre la cantidad de abejas macho y abejas hembra en un panal.
- La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).
- La distribución de las hojas en un tallo. Ver: Sucesión de Fibonacci.
- La relación entre las nervaduras de las hojas de los árboles
- La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).
- La distancia entre las espirales de una Piña.
- La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol o de cefalópodos como el nautilus. Hay por lo menos tres espirales logarítmicas más o menos asimilables a proporciones aúreas. La primera de ellas se caracteriza por la relación constante igual al número áureo entre los radiovectores de puntos situados en dos evolutas consecutivas en una misma dirección y sentido. Las conchas del Fusus antiquus, del Murex, de Scalaria pretiosa, de Facelaria y de Solarium trochleare, entre otras, siguen este tipo de espiral de crecimiento.[8] [9] Se debe entender que en toda consideración natural, aunque involucre a las ciencias consideradas más matemáticamente desarrolladas, como la Física, ninguna relación o constante que tenga un número infinito de decimales puede llegar hasta el límite matemático, porque en esa escala no existiría ningún objeto físico. La partícula elemental más diminuta que se pueda imaginar es infinitamente más grande que un punto en una recta. Las leyes observadas y descriptas matemáticamente en los organismos las cumplen transgrediéndolas orgánicamente.[10]
- Para que las hojas esparcidas de una planta (Ver Filotaxis) o las ramas alrededor del tronco tengan el máximo de insolación con la mínima interferencia entre ellas, éstas deben crecer separadas en hélice ascendente según un ángulo constante y teóricamente igual a 360º (2 - φ) ≈ 137º 30' 27,950 580 136 276 726 855 462 662 132 999..." En la naturaleza se medirá un ángulo práctico de 137º 30' o de 137º 30' 28" en el mejor de los casos. Para el cálculo se considera iluminación vertical y el criterio matemático es que las proyecciones horizontales de unas sobre otras no se recubran exactamente. Aunque la iluminación del Sol no es, en general, vertical y varía con la latitud y las estaciones, esto garantiza el máximo aprovechamiento de la luz solar. Este hecho fue descubierto empíricamente por Church y confirmado matemáticamente por Weisner en 1875. En la práctica no puede medirse con tanta precisión el ángulo y las plantas lo reproducen "orgánicamente"; o sea, con una pequeña desviación respecto al valor teórico.
- En la cantidad de elementos constituyentes de las espirales o dobles espirales de las inflorescencias, como en el caso del girasol, y en otros objetos orgánicos como las piñas de los pinos se encuentran números pertenecientes a la sucesión de Fibonacci. El cociente de dos números sucesivos de esta sucesión tiende al número áureo.
- Existen cristales de Pirita dodecaédricos pentagonales (piritoedros) cuyas caras son pentágonos irregulares. Sin embargo, las proporciones de dicho poliedro irregular no involucran el número áureo.
- El número áureo en el cine:
El número Fi aparece en la película de Disney "Donald en el país de las Matemágicas"
[editar] El número áureo en el ser humano
| Existen desacuerdos sobre la neutralidad en el punto de vista de la versión actual de este artículo o sección. En la página de discusión puedes consultar el debate al respecto. |
- La Anatomía de los humanos se basa en una relación Φ estadística y aproximada, así vemos que:
- La relación entre la altura de un ser humano y la altura de su ombligo.
- La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
- La relación entre la altura de la cadera y la altura de la rodilla.
- La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es Φ.
- La relación entre el diámetro de la boca y el de la nariz
- Es Φ la relación entre el diámetro externo de los ojos y la línea inter-pupilar
- Cuando la tráquea se divide en sus bronquios, si se mide el diámetro de los bronquios por el de la tráquea se obtiene Φ, o el de la aorta con sus dos ramas terminales (ilíacas primitivas).
[editar] El número áureo en el Arte
| Existen desacuerdos sobre la neutralidad en el punto de vista de la versión actual de este artículo o sección. En la página de discusión puedes consultar el debate al respecto. |
- Relaciones en la forma de la Gran Pirámide de Gizeh. La afirmación de Heródoto de que el cuadrado de la altura es igual a la superficie de una cara es posible únicamente si la semi-sección meridiana de la pirámide es proporcional al triángulo rectángulo
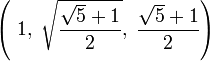 , donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice (inexistente en la actualidad) y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), se apoya en la interpretación de un pasaje de Heródoto (Historiae, libro II, cap. 124) y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre π. Pero una construcción tal, aunque se conociera π con una aproximación grande, carecería completamente de interés geométrico.[11] No obstante, con base en mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades.
, donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice (inexistente en la actualidad) y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), se apoya en la interpretación de un pasaje de Heródoto (Historiae, libro II, cap. 124) y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre π. Pero una construcción tal, aunque se conociera π con una aproximación grande, carecería completamente de interés geométrico.[11] No obstante, con base en mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades.
- La relación entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.).Durante el primer cuarto del siglo XX, Jay Hambidge, de la Universidad de Yale, se inspiró en un pasaje del Teeteto de Platón para estudiar las proporciones relativas de las superficies, algo muy natural cuando se trata de obras arquitectónicas. Dos rectángulos no semejantes se distinguen entre sí por el cociente de su lado mayor por el menor, número que basta para caracterizar a estas figuras y que denominó módulo del rectángulo. Un cuadrado tiene módulo 1 y el doble cuadrado módulo 2. Aquellos rectángulos cuyos módulos son números enteros o racionales fueron denominados "estáticos" y los que poseen módulos irracionales euclidianos, o sea, expresables algebraicamente como raíces de ecuaciones cuadráticas o reducibles a ellas, "dinámicos". El doble cuadrado es a la vez estático y dinámico, pues 2 es la raíz cuadrada de 4. Un ejemplo de rectángulo dinámico elemental es aquel que tiene por lado mayor a la raíz cuadrada de 5 y por lado menor a la unidad, siendo su módulo la raíz cuadrada de 5.[12] Posteriormente Hambidge estudió a los monumentos y templos griegos y llegó a encuadrar el frontón del Partenón en un rectángulo de módulo
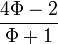 . Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo
. Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo 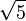 y cuatro cuadrados.[13] Como dato adicional para indicar la complejidad del tratamiento del edificio se tiene que en 1837 fueron descubiertas correcciones ópticas en el Partenón. El templo tiene tres vistas principales y si sus columnas estuvieran efectivamente a plomo, todas sus líneas fuesen paralelas y perfectamente rectas y los ángulos rectos fueran exactos, por las propiedades de la visión humana el conjunto se vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columnas se vería como una especie de catenaria, con los extremos del edificio aparentemente más altos que el centro. Los constructores hicieron la construcción compensando estos efectos de ilusión óptica inclinando o curvando en sentido inverso a los elementos involucrados. Así las columnas exteriores, en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. De esta forma, y con otras correcciones que no se mencionan aquí, se logra que cualquier observador que se sitúe en los tres puntos principales de vista vea todo el conjunto paralelo, uniforme y recto.[14]
y cuatro cuadrados.[13] Como dato adicional para indicar la complejidad del tratamiento del edificio se tiene que en 1837 fueron descubiertas correcciones ópticas en el Partenón. El templo tiene tres vistas principales y si sus columnas estuvieran efectivamente a plomo, todas sus líneas fuesen paralelas y perfectamente rectas y los ángulos rectos fueran exactos, por las propiedades de la visión humana el conjunto se vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columnas se vería como una especie de catenaria, con los extremos del edificio aparentemente más altos que el centro. Los constructores hicieron la construcción compensando estos efectos de ilusión óptica inclinando o curvando en sentido inverso a los elementos involucrados. Así las columnas exteriores, en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. De esta forma, y con otras correcciones que no se mencionan aquí, se logra que cualquier observador que se sitúe en los tres puntos principales de vista vea todo el conjunto paralelo, uniforme y recto.[14]
- En el cuadro Leda atómica de Salvador Dalí, hecho en colaboración con el matemático rumano Matila Ghyka.
- En los violines, la ubicación de las efes (los “oídos”, u orificios en la tapa) se relaciona con el número áureo.
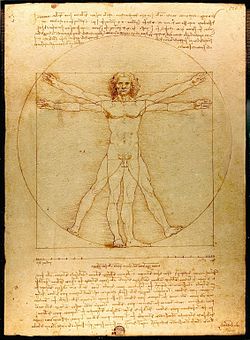
- El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Leonardo Da Vinci, entre otros.
- Las relaciones entre articulaciones en el hombre de Vitruvio y en otras obras de Leonardo da Vinci.
- En las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Debussý (estos compositores probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras).
- En la pág. 56 de la novela de Dan Brown El código Da Vinci aparece una versión desordenada de los primeros ocho números de Fibonacci (13, 3, 2, 21, 1, 1, 8, 5), que funcionan como una pista dejada por el curador del museo del Louvre, Jacques Saunière. En las pp. 121 a 123 explica algunas de las apariciones de este número fi (1,618) en la naturaleza.
- En el episodio “Sabotaje” de la serie de televisión NUMB3RS (primera temporada, 2005), el genio de la matemática Charlie Eppes menciona que el número fi se encuentra en la estructura de los cristales, en la espiral de las galaxias y en la concha del nautilus.
- Arte Póvera, movimiento artístico italiano de los años 1960, muchas de cuyas obras se basan en esta sucesión.
- En la cinta de Darren Aronofsky Pi, fe en el caos el personaje central, Max Cohen, explica la relación que hay entre los números de Fibonacci y la sección áurea, aunque denominándola incorrectamente como Theta (θ) en vez de Phi (Φ).
[editar] El número áureo en el misticismo
En la cruz latina, símbolo del catolicismo, la relación entre el palo vertical y el horizontal es el número áureo. Así mismo, el palo horizontal divide al vertical en secciones áureas. [cita requerida]
[editar] Véase también
- Número π
- Espiral logarítmica
- Estrella mágica
- Sucesión de Fibonacci
- Composición áurea
- Pitágoras
- Luca Pacioli
- Matila Ghyka
- Roger Penrose
- Decágono regular
[editar] Referencias
- ↑ Fernando Corbalán (2010). La proporción áurea. RBA Coleccionables S. A.. ISBN 978-84-473-6623-1.
- ↑ Este número es irracional, aunque es algebraico y también constructible mediante regla y compás, y existen numerosas aproximaciones racionales con mayor o menor error. En el año 2008 se obtuvieron cien mil millones de cifras decimales correctas. (Ver: http://numbers.computation.free.fr/Constants/Miscellaneous/Records.html) Al igual que ocurre con la raíz cuadrada de dos, es posible construir un segmento idealmente exacto con regla no graduada de un solo borde y longitud indefinida y un compás de abertura variable. ¿Qué significa esto? Que ningún dibujo puede ser tan fino como para representar el concreto y real valor puntual del número áureo. Cualquier objeto construido por el hombre o formado naturalmente, aunque se tuviera la intención manifiesta de lograr una representación de ese número, llevaría consigo un error inevitable. Un segmento de recta tan pequeño como el diámetro aparente de la partícula atómica más pequeña tiene tantos puntos geométricos como toda la recta. Con todo, la construcción geométrica es idealmente exacta y por este motivo se estimó durante un tiempo considerable a la geometría como superior a la aritmética. La diferencia está en que el valor aritmético está dado como un infinito potencial y el valor geométrico como un infinito actual, generando un segmento de recta constructible.
- ↑ Proporción Áurea en WolframMathWorld
- ↑ Mario Livio (2002). The Golden Ratio. Broadway Books. ISBN 0-7679-0816-3.
- ↑ Bad approximable numbers in WolframMathWorld
- ↑ Trabajo presentado por Mark Barr y Shooling en la revista The Field del 14 de diciembre de 1912.
- ↑ N. N. Vorobiov; traducción de Carlos vega (1974). Números de Fibonacci. Editorial Mir, Moscú, rústica, 112 páginas.
- ↑ Matila Ghyka (1953). Estética de las Proporciones en la Naturaleza y en las Artes. Editorial Poseidón, Buenos Aires, Capítulo V: "Del Crecimiento Armonioso", páginas 118 a 144.
- ↑ D'Arcy Wentworth Thompson (1917). "On Growth and Form". Cambridge University Press. D'Arcy Wentworth Thompson (1992). "On Growth and Form". Dover edition, 1116 páginas. D'Arcy Thompson (1980). "Sobre el Crecimiento y la Forma. Editorial Hermann Blume, Madrid.Existen ediciones de unas 300 páginas, una reciente de Cambridge.
- ↑ Es una paráfrasis de un pensamiento de Ruskin mencionado en la página 139 del libro citado de Matila Ghyka
- ↑ "Lógicamente, la tesis de la sección áurea parecería más probable, porque de ella emana una construcción rigurosa, elegante y sencilla del triángulo meridiano, mientras que en la otra hipótesis, aún suponiendo conocido con una aproximación muy grande el valor de π, la construcción sería puramente empírica y desprovista de verdadero interés geométrico" [Es notable, además, que aunque los antiguos no sabían de la trascendencia de π, estaban completamente conscientes de la carencia de exactitud de algunos intentos de cuadratura del círculo] Matila Ghyka (1953). Estética de las Proporciones en la Naturaleza y en las Artes. Editorial Poseidón, Buenos Aires, Capítulo VIII: "La Pirámide de Keops", página 222.
- ↑ Jay Hambidge (1920; 1930; 1931). "Dynamic Symmetry The Greek Vase". Yale University Press, New Haven.Jay Hambidge (22/08/2007). Dynamic Symmetry The greek vase. Rough Draf Printing. ISBN 978-1-60386-037-6.
- ↑ Jay Hambidge (1924). "The Parthenon and Other Greek temples, their Dynamic Symmetry". Yale University Press, New haven. Hay todavía disponibles ejemplares de esa edición, tanto nuevos como usados y a la venta a aproximadamente $ (USA) 250.
- ↑ Banister; Fletcher. "A History of Architecture". B. T. Basford, Londres.
[editar] Bibliografía
En orden cronológico:
- Jarolimek (Viena, 1890). Der Mathematischen Schlüssel zu der Pyramide des Cheops.
- Kleppisch, K. (1921). Die Cheops-Pyramide: Ein Denkmal Mathematischer Erkenntnis. Múnich: Oldenburg.
- Cook, Theodore Andrea (1979; obra original: 1914). The Curves of Live. Nueva York: Dover. ISBN 0-486-23701-X; ISBN 978-0-486-23701-5.
- Pacioli, Luca (1991). La Divina Proporción. Tres Cantos: Ediciones Akal, S. A.. ISBN 978-84-7600-787-7.
- Ghyka, Matila (1992). El Número de Oro. Barcelona: Poseidón, S.L.. ISBN 978-84-85083-11-4.
- Ghyka, Matila (2006). El Número de Oro. I Los ritmos. II Los Ritos. Madrid: Ediciones Apóstrofe, S. L.. ISBN 978-84-455-0275-4.
- Corbalán, Fernando (2010). La proporción áurea. RBA Coleccionables S. A.. ISBN 978-84-473-6623-1.
[editar] Enlaces externos
 Wikimedia Commons alberga contenido multimedia sobre Número áureo. Commons
Wikimedia Commons alberga contenido multimedia sobre Número áureo. Commons- Astronomy.swin.edu.au (Fi, la sección áurea).
- ChampionTrees.org (Fi: la proporción divina).
- GoldenRatio.com.ar (propiedades interesantes del número áureo y aplicación en la biología).
- MCS.Surrey.ac.uk (La sección áurea: fi).
- MathWorld.Wolfram.com/GoldenRatio.html (la sección áurea).
- Rt000z8y.EresMas.net (una buena página que explica Φ detalladamente]
- Rt000z8y.EresMas.net (más ejemplos de Φ en la vida).
- Castor.es (El número Fi en la arquitectura, pintura, animales, plantas etc.)
- Gráficas de sucesiones áureas en MATLAB
- Gráficas de sucesiones áureas en MATLAB II
- El número de Oro - La Razón Aurea
- http://www.palermo.edu/ingenieria/downloads/Investigacion/ElNumeroyloSagrado1P.pdf
Obtenido de "http://es.wikipedia.org/wiki/N%C3%BAmero_%C3%A1ureo"
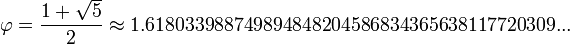
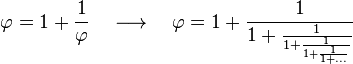


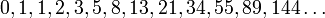

 quedan definidos por las ecuaciones
quedan definidos por las ecuaciones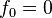
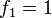
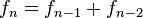 para
para 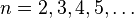
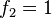
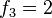
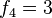
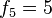
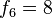
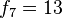
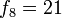
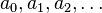 es la función
es la función 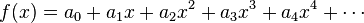 , es decir, una
, es decir, una 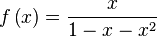
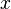 , los coeficientes resultan ser la sucesión de Fibonacci:
, los coeficientes resultan ser la sucesión de Fibonacci: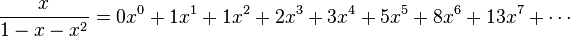
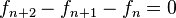
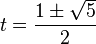
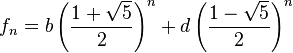
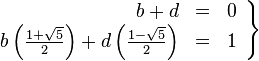
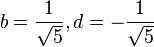
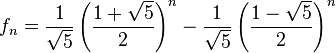
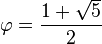
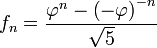
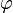 . De hecho, la relación con este número es estrecha.
. De hecho, la relación con este número es estrecha.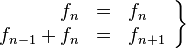
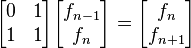
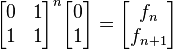
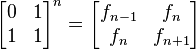
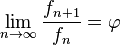
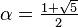 y
y 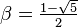 , entonces
, entonces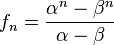 y
y 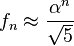
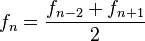
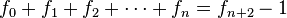
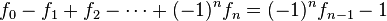
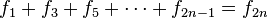
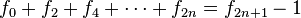
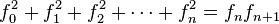
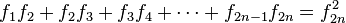
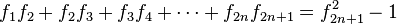
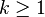 , entonces
, entonces 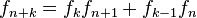 para cualquier
para cualquier 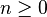
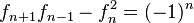 (Identidad de
(Identidad de 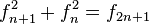
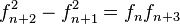
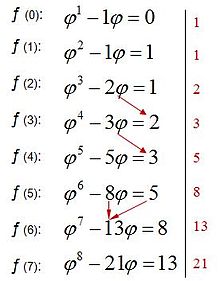
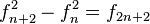
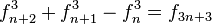
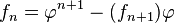 (con φ = número áureo)
(con φ = número áureo)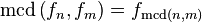 Esto significa que
Esto significa que 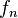 y
y 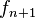 son
son 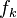
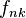
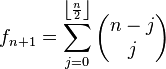 y más aún
y más aún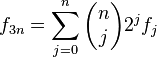
 es exactamente
es exactamente  .
. números.
números.
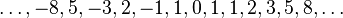 de manera que la suma de cualesquiera dos números consecutivos es el inmediato siguiente. Para poder definir los índices negativos de la sucesión, se despeja
de manera que la suma de cualesquiera dos números consecutivos es el inmediato siguiente. Para poder definir los índices negativos de la sucesión, se despeja 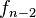 de la ecuación (
de la ecuación (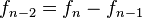
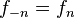 si
si 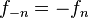 si
si 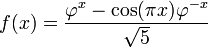
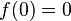
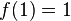
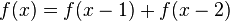 para cualquier número real
para cualquier número real 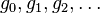 donde
donde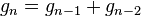 para
para 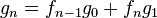
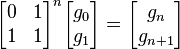
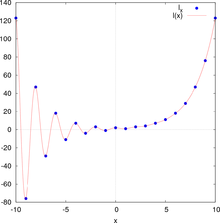
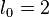
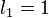
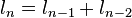 para
para 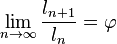
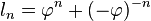
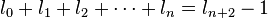
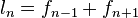
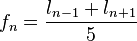
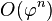 )
)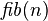
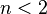 entonces devuelve
entonces devuelve 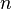 si no devuelve
si no devuelve 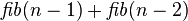
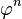 , entonces el algoritmo está en el orden de
, entonces el algoritmo está en el orden de 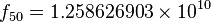 aun cuando el resultado correcto es
aun cuando el resultado correcto es 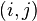 de números consecutivos de la sucesión de Fibonacci, el siguiente par de la sucesión es
de números consecutivos de la sucesión de Fibonacci, el siguiente par de la sucesión es 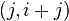 , de esta manera se divisa un algoritmo donde sólo se requiere considerar dos números consecutivos de la sucesión de Fibonacci en cada paso. Este método es el que usaríamos normalmente para hacer el cálculo a lápiz y papel. El algoritmo se expresa en pseudocódigo como:
, de esta manera se divisa un algoritmo donde sólo se requiere considerar dos números consecutivos de la sucesión de Fibonacci en cada paso. Este método es el que usaríamos normalmente para hacer el cálculo a lápiz y papel. El algoritmo se expresa en pseudocódigo como: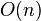 )
)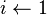
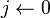 para
para 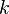 desde
desde 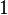 hasta
hasta 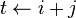
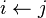
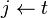 devuelve
devuelve 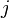

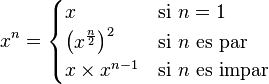
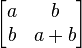
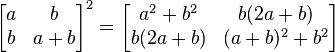
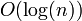 )
)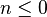 entonces devuelve
entonces devuelve 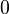
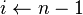
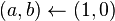
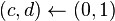 mientras
mientras  hacer si
hacer si  es impar entonces
es impar entonces 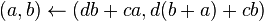
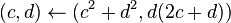
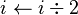 devuelve
devuelve 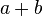

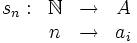
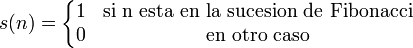

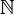 en X.
en X.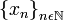 a una sucesión, donde x la identifica como distinta de otra digamos
a una sucesión, donde x la identifica como distinta de otra digamos 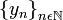 .
.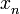 ,donde
,donde 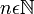 indica el lugar que ocupa en dicha sucesión.
indica el lugar que ocupa en dicha sucesión.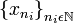 donde
donde 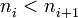
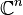
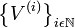 tal que
tal que 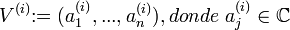
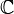
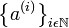 tal que
tal que 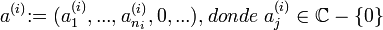
![P(x) in K[x]](https://petalofucsia.blogia.com/upload/externo-ea4d2efb88ad533e87e6b272aeb126cb.png) no es más que una sucesión finita
no es más que una sucesión finita 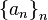 tal que
tal que 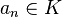 representada como
representada como 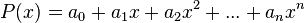 .
.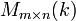
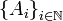 tal que
tal que 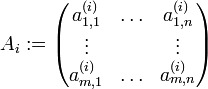 , donde
, donde 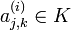 .
.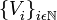 , donde
, donde 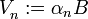 , donde
, donde 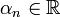 es una sucesión real arbitraria y B un abierto.
es una sucesión real arbitraria y B un abierto.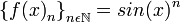 .
.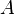 un alfabeto, llamaremos
un alfabeto, llamaremos 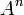 al conjunto de sucesiones finitas de n elementos de
al conjunto de sucesiones finitas de n elementos de 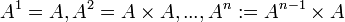
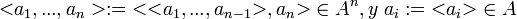 .
.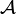 una categoría, podemos tener una sucesión
una categoría, podemos tener una sucesión 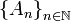 , donde
, donde 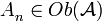 .
.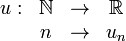
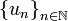 o, si se da por entendido que los subíndices son enteros, también vale
o, si se da por entendido que los subíndices son enteros, también vale 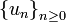 .
.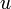 fuesen los racionales, es decir fracciones enteras del tipo
fuesen los racionales, es decir fracciones enteras del tipo 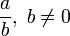 , podemos llamarla sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, ... .
, podemos llamarla sucesión de números racionales, y lo mismo para los irracionales, naturales, enteros, algebraicos, trascendentes, ... .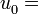 a por ejemplo 3,
a por ejemplo 3,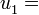 a por ejemplo -10,
a por ejemplo -10,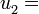 a por ejemplo 9, y así sucesivamente.
a por ejemplo 9, y así sucesivamente.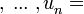 a por ejemplo número al azar, ... .
a por ejemplo número al azar, ... .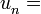 , el portador del método para generar el valor de cada término, y el nombre
, el portador del método para generar el valor de cada término, y el nombre 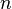 puede ser cambiado, si hace falta, por
puede ser cambiado, si hace falta, por 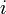 ,
, 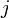 ,
, 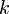 ,
, 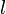 , ... .
, ... .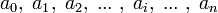 , donde
, donde 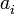 sería el término general si hiciese falta.ejemplo: 100, 99, 98, ... , 1, 0.
sería el término general si hiciese falta.ejemplo: 100, 99, 98, ... , 1, 0.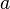 , un número real cualquiera, ejemplo:
, un número real cualquiera, ejemplo: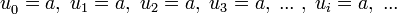 .ejemplo: si
.ejemplo: si 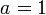 queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.
queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1.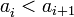 , es decir, que el siguiente término,
, es decir, que el siguiente término, 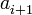 , siempre sea mayor estricto que su predecesor,
, siempre sea mayor estricto que su predecesor, 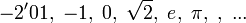 .
.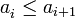 , es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.
, es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.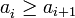 entonces la sucesión es decreciente,
entonces la sucesión es decreciente,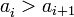 es estrictamente decreciente.
es estrictamente decreciente.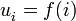 donde
donde 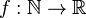 es una función cualquiera como por ejemplos:
es una función cualquiera como por ejemplos: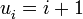 que daría la sucesión de naturales sucesivos, es decir, 1, 2, 3, 4, 5, ... .
que daría la sucesión de naturales sucesivos, es decir, 1, 2, 3, 4, 5, ... .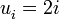 que daría todos los número pares incluido el cero, es decir, 0, 2, 4, 6, 8, ... .
que daría todos los número pares incluido el cero, es decir, 0, 2, 4, 6, 8, ... .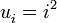 que daría la sucesión de cuadrados siguiente, 0, 1, 4, 9, 16, ... .
que daría la sucesión de cuadrados siguiente, 0, 1, 4, 9, 16, ... .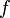 a una función
a una función 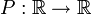 cuyos valores coinciden en el dominio de
cuyos valores coinciden en el dominio de 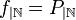 .
.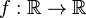 !, pues, se trata de una asociación totalmente arbitraria y no univoca que trae confusión y no tiene sentido para algunas
!, pues, se trata de una asociación totalmente arbitraria y no univoca que trae confusión y no tiene sentido para algunas 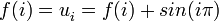 solo si la sucesión que determinan sobre los enteros es la misma, pero ¡no son la misma función!, llamemos a la extendida por ejemplo
solo si la sucesión que determinan sobre los enteros es la misma, pero ¡no son la misma función!, llamemos a la extendida por ejemplo  o
o  si es un polinomio, o
si es un polinomio, o 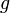 o
o 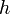 si son funciones trigonométricas, agregando subíndices si hace falta.
si son funciones trigonométricas, agregando subíndices si hace falta.
 , podemos definir el término general de forma
, podemos definir el término general de forma 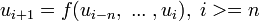 como por ejemplo con la ecuación en diferencias
como por ejemplo con la ecuación en diferencias 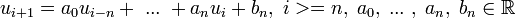 .
.


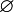 es un elemento de la colección, si la unión de elementos de la colección da como resultado un elemento de la colección y si la intersección finita de elementos de la colección también es un elemento de la colección. A los elementos de la colección
es un elemento de la colección, si la unión de elementos de la colección da como resultado un elemento de la colección y si la intersección finita de elementos de la colección también es un elemento de la colección. A los elementos de la colección 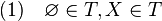
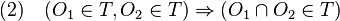
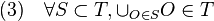
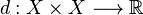 que verifica las siguientes propiedades:
que verifica las siguientes propiedades: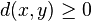 ;
;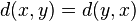
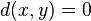 si y sólo si
si y sólo si 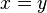 ;
;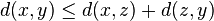
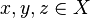 .
.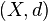
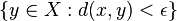 está totalmente incluido en
está totalmente incluido en 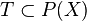 que cumpla que
que cumpla que 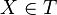 ,
, 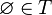 , si
, si 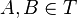 entonces
entonces 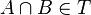 , y que si
, y que si 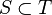 entonces
entonces 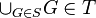 . A los elementos de
. A los elementos de 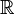 o en
o en 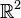 o
o 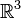 cumplen las condiciones exigibles a una topología. Es precisamente el comprobar que otras familias de conjuntos en otros conjuntos de naturaleza no geométrica que comparten estas mismas propiedades (como en el conjunto de soluciones de una ecuación diferencial, o el conjunto de los ceros de los polinomios con coeficientes en los ideales en un anillo conmutativo, por ejemplo) lo que motiva esta definición. Así podremos aplicar a estos conjuntos las mismas (o parecidas) técnicas topológicas que aplicamos a los abiertos del plano, por ejemplo. La situación es análoga a la que se da en Álgebra Lineal cuando se pasa de trabajar en
cumplen las condiciones exigibles a una topología. Es precisamente el comprobar que otras familias de conjuntos en otros conjuntos de naturaleza no geométrica que comparten estas mismas propiedades (como en el conjunto de soluciones de una ecuación diferencial, o el conjunto de los ceros de los polinomios con coeficientes en los ideales en un anillo conmutativo, por ejemplo) lo que motiva esta definición. Así podremos aplicar a estos conjuntos las mismas (o parecidas) técnicas topológicas que aplicamos a los abiertos del plano, por ejemplo. La situación es análoga a la que se da en Álgebra Lineal cuando se pasa de trabajar en 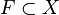 se dice que es cerrado si su complementario
se dice que es cerrado si su complementario 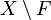 es un conjunto abierto. Es importante observar que un conjunto que no es abierto no necesariamente ha de ser cerrado, y un conjunto que no sea cerrado no necesariamente ha de ser abierto. Así, existen conjuntos que son abiertos y cerrados a la vez, como
es un conjunto abierto. Es importante observar que un conjunto que no es abierto no necesariamente ha de ser cerrado, y un conjunto que no sea cerrado no necesariamente ha de ser abierto. Así, existen conjuntos que son abiertos y cerrados a la vez, como 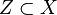 , el conjunto
, el conjunto 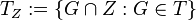 es una topología para
es una topología para 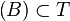 se dice que es
se dice que es 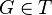 existe un conjunto
existe un conjunto 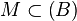 de manera que
de manera que 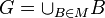 .
.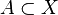 un conjunto cualquiera y sea
un conjunto cualquiera y sea 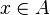 un punto arbitrario. Se dice que
un punto arbitrario. Se dice que 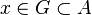 . Todo conjunto abierto es entorno de todos sus puntos. Al conjunto de todos los entornos de un punto
. Todo conjunto abierto es entorno de todos sus puntos. Al conjunto de todos los entornos de un punto 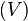 de entornos de un mismo punto x se dice que es una base de entornos (o base local) de
de entornos de un mismo punto x se dice que es una base de entornos (o base local) de 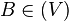 de manera que
de manera que 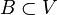 .
.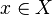 se dirá que es un punto interior de
se dirá que es un punto interior de 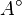 . Es el mayor conjunto abierto incluido en A.
. Es el mayor conjunto abierto incluido en A.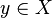 se dirá que es un punto exterior a
se dirá que es un punto exterior a 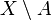 es entorno de
es entorno de 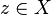 se dice que es un punto frontera de
se dice que es un punto frontera de 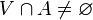 y
y 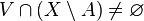 . Al conjunto de los punto frontera de
. Al conjunto de los punto frontera de 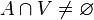 . Se hace pues evidente que todo punto interior y todo punto frontera es punto de adherencia. Al conjunto de los puntos de adherencia del conjunto
. Se hace pues evidente que todo punto interior y todo punto frontera es punto de adherencia. Al conjunto de los puntos de adherencia del conjunto 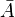 . La clausura de un conjunto
. La clausura de un conjunto 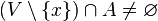 . Al conjunto de los puntos de acumulación de un conjunto se le denomina acumulación del conjunto, o conjunto derivado, y se le denota por
. Al conjunto de los puntos de acumulación de un conjunto se le denomina acumulación del conjunto, o conjunto derivado, y se le denota por 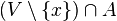 es un conjunto infinito. Al conjunto de los puntos de
es un conjunto infinito. Al conjunto de los puntos de 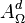 o por
o por 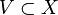 de manera que
de manera que 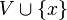 es un entorno de
es un entorno de 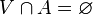 . Al conjunto de los puntos aislados de
. Al conjunto de los puntos aislados de 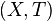 es una aplicación
es una aplicación 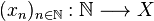 .
.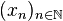 , o bien que
, o bien que 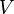 de
de 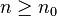 ) entonces se cumple que
) entonces se cumple que 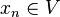 .
.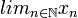 , o también por
, o también por 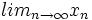 ).
).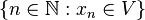 es infinito. Todo punto límite es punto de aglomeración, pero el recíproco no es cierto. Por ejemplo, los
es infinito. Todo punto límite es punto de aglomeración, pero el recíproco no es cierto. Por ejemplo, los 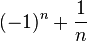 ) son puntos de aglomeración, pero no son puntos límites (no existe límite para dicha sucesión, mientras que 1 y -1 son puntos de acumulación).
) son puntos de aglomeración, pero no son puntos límites (no existe límite para dicha sucesión, mientras que 1 y -1 son puntos de acumulación).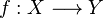 entre dos espacios topológicos se dice que es continua si dado cualquier conjunto
entre dos espacios topológicos se dice que es continua si dado cualquier conjunto  abierto en
abierto en 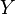 , el conjunto
, el conjunto 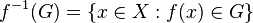 es un conjunto abierto en
es un conjunto abierto en 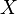 .
.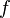 es continua en
es continua en 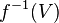 es un entorno de
es un entorno de 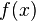 .
.![,forall x,y in X quad exist phi : [0,1] longrightarrow X](https://petalofucsia.blogia.com/upload/externo-405eaffdfe979c9faf10d706ac40413e.png) continua de tal manera que
continua de tal manera que 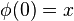 y
y 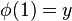 . Todo conjunto conexo por caminos es conexo, pero no todo conjunto conexo es conexo por caminos.
. Todo conjunto conexo por caminos es conexo, pero no todo conjunto conexo es conexo por caminos.
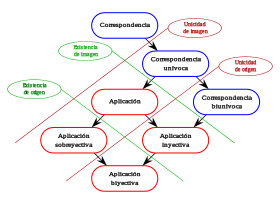
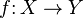










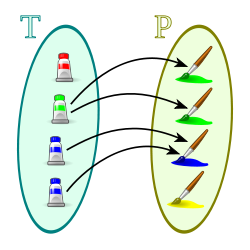
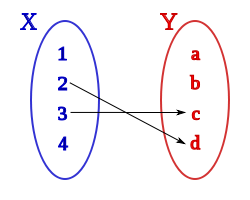
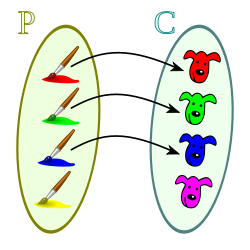
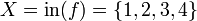
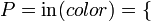
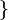
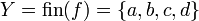
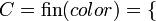
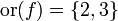
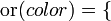
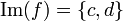
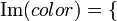
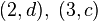
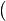
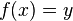
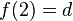
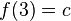
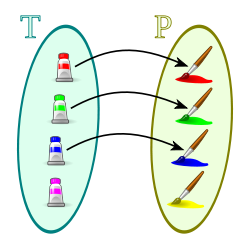
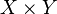 , de estos dos conjuntos, como el conjunto de
, de estos dos conjuntos, como el conjunto de 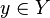 , dado el conjunto F que contiene a los pares homónimos de la correspondencia f, y
, dado el conjunto F que contiene a los pares homónimos de la correspondencia f, y 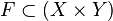 define esa correspondencia en su totalidad.
define esa correspondencia en su totalidad.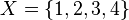
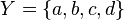
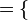
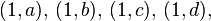
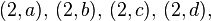
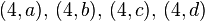
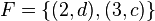
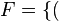
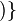
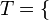
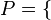
















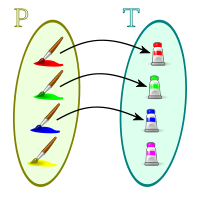
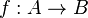
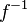 :
: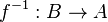
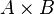 , donde los pares ordenados (a, b) son los asociados por la correspondencia, la correspondencia inversa
, donde los pares ordenados (a, b) son los asociados por la correspondencia, la correspondencia inversa 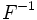 , es el subconjunto del producto cartesiano
, es el subconjunto del producto cartesiano 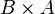 , formado por los pares ordenados (b, a) obtenidos de cambiar el orden de la correspondencia F.
, formado por los pares ordenados (b, a) obtenidos de cambiar el orden de la correspondencia F.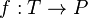
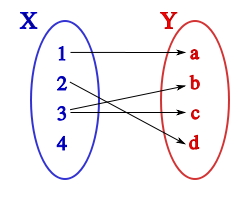
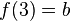
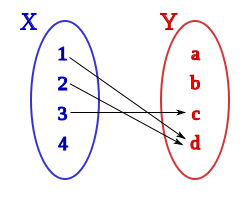
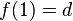
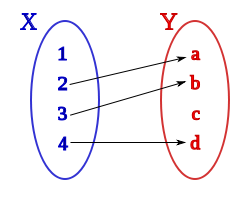
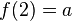
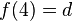
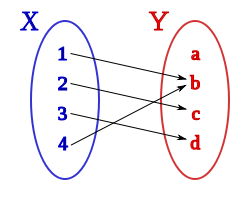
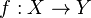
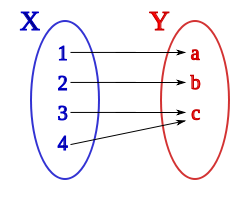
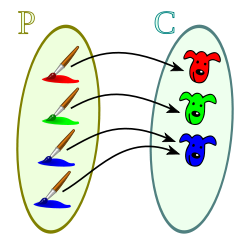
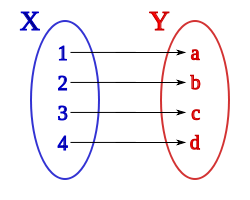
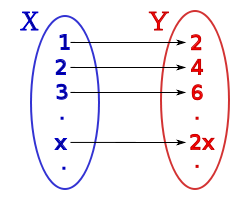
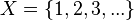
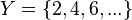
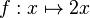








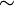
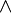
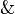
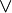

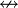
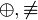
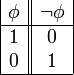
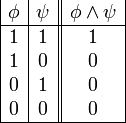
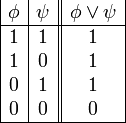
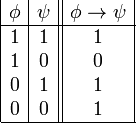
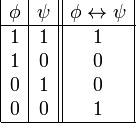
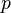
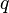
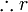
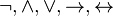
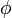 es una fórmula bien formada de L, entonces
es una fórmula bien formada de L, entonces 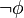 también lo es.
también lo es.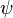 son fórmulas bien formadas de L, entonces
son fórmulas bien formadas de L, entonces 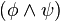 ,
, 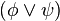 ,
, 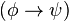 y
y 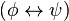 también lo son.
también lo son.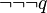
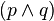
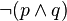
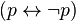
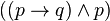
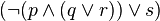
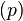
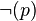
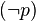
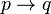
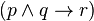
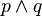
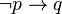
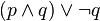
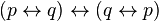
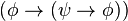
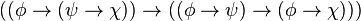
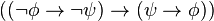
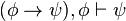
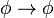
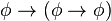
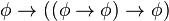
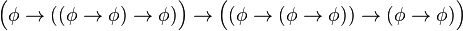
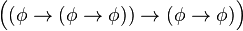
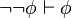
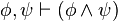
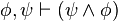
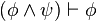
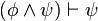
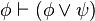
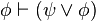
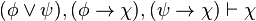
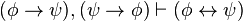
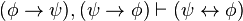
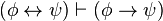
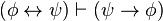
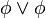
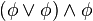
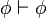
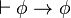
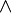 )
)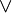 )
)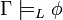
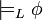
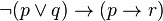 sería:
sería: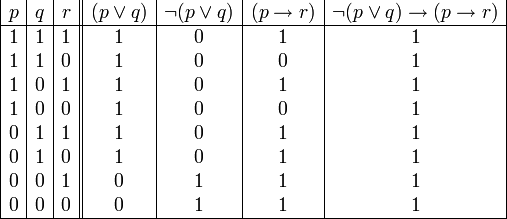
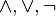 ). Para lograr esto se utilizan las equivalencias logicas:
). Para lograr esto se utilizan las equivalencias logicas: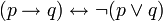
![(p leftrightarrow q) leftrightarrow [neg (p or q) and neg (q or p)]](https://petalofucsia.blogia.com/upload/externo-f30d1590c304e89e83da62d2b9546add.png)
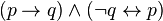
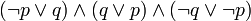
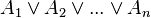
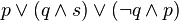
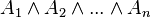
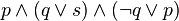
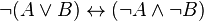
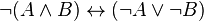
![neg [(A_1 and B_1) or (A_2 and B_2) or ... or (A_n and B_n)] leftrightarrow [(neg A_1 or neg B_1) and (neg A_2 or neg B_2) and ... and (neg A_n or neg B_n)](https://petalofucsia.blogia.com/upload/externo-47dbd37db04f99e72c539dc8ff4593c7.png)
![neg [(A_1 or B_1) and (A_2 or B_2) and ... and (A_n or B_n)] leftrightarrow [(neg A_1 and neg B_1) or (neg A_2 and neg B_2) or ... or (neg A_n and neg B_n)](https://petalofucsia.blogia.com/upload/externo-ae192a8a67f7be187df1c063245bf4eb.png)