MATEMÁTICAS4: LA ESCRITURA DE LA GENTE, MUESTRA "VARIACIONES" DE PERSONA A PERSONA, NO ES EXACTA. ESTO CONSISTE EN ELEVAR A LAS POTENCIAS (ALGO QUE IBA A SUCEDER CON EL DNA). En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto. EJEMPLO: Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
Permutación
En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.
Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
La noción de permutación suele aparecer en dos contextos:
- Como noción fundamental de combinatoria, centrándonos en el problema de su recuento.
- En teoría de grupos, al definir nociones de simetría.
Contenido[ocultar] |
[editar] Definición alternativa
La permutación antes citada "1,3,2" puede verse como la imagen de una aplicación σ de la lista inicial de objetos (1, 2, 3) en la lista de objetos reordenados (1, 3, 2). De este modo σ(1)=1, σ(2)=3 y σ(3)=2. También podemos definir a la permutación como la propia aplicación σ.
Así, formalmente, una permutación de un conjunto X es una biyección de X en sí mismo.
Aunque esta segunda definición generaliza a la primera al admitir conjuntos infinitos, el término permutación se usa principalmente para un conjunto finito X, y así lo haremos en el resto del artículo.
[editar] En combinatoria
La combinatoria trata del número de diferentes maneras que existen de considerar conjuntos formados a partir de elementos de un conjunto dado, respetando ciertas reglas. Así un problema combinatorio consiste usualmente en establecer una regla sobre cómo deben ser las combinaciones y determinar cuántas existen que cumplan dicha regla.
Un tipo importante de esas combinaciones son las llamadas permutaciones. Dada una n-tupla ordenada de elementos de un conjunto, el número de permutaciones es el número de n-tuplas ordenadas .
[editar] Recuento del número de permutaciones
Dado un conjunto finito y ordenado 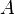 de
de 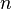 elementos, el número de permutaciones diferentes posibles es igual a la factorial de n:
elementos, el número de permutaciones diferentes posibles es igual a la factorial de n: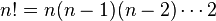 .
.
Dado que hay 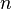 formas de escoger el primer elemento y, una vez escogido éste, sólo tenemos
formas de escoger el primer elemento y, una vez escogido éste, sólo tenemos 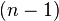 formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos
formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos 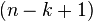 posibles elementos para escoger, lo que nos lleva a que tenemos
posibles elementos para escoger, lo que nos lleva a que tenemos 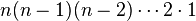 formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.
formas de ordenar el conjunto, justamente lo que enunciamos anteriormente. 
[editar] Recuento del número de conjuntos ordenados de k elementos con k<n
Dado un conjunto A finito de cardinal n, tenemos 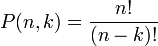 formas de construir un conjunto ordenado B de k elementos donde
formas de construir un conjunto ordenado B de k elementos donde 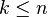 .
.
A éste número se le llama permutaciones de n en k. Otras notaciones son 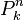 o
o ![left[{natop k}right]](https://petalofucsia.blogia.com/upload/externo-f0e7cec9be951a0596774e8298c3d5db.png) (en algunas partes del mundo se le conoce como variaciones y se denota
(en algunas partes del mundo se le conoce como variaciones y se denota 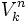 ).
).
Basta demostrar que las permutaciones están ligadas al coeficiente binomial mediante la siguiente identidad:
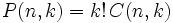
Para ello, dado que el coeficiente binomial es la cantidad de conjuntos finitos de k elementos formados a partir de los elementos de un conjunto de n elementos, donde 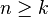 y cualquier conjunto finito con cardinal k se puede ordenar de k! maneras diferentes.
y cualquier conjunto finito con cardinal k se puede ordenar de k! maneras diferentes. 
Observamos que para k=n recuperamos la fórmula de recuento de permutaciones y que para k=1, P(n,1)=n.
[editar] En teoría de grupos
[editar] Notaciones
La primera forma de escribir una permutación σ, aunque no es la más compacta, consiste en escribirla en forma de matriz de dos filas, situando en la primera fila los elementos del dominio 1, 2, 3,...,n, y en la segunda las imágenes correspondientes a los elementos reordenados σ(1), σ(2), σ(3),...,σ(n).
Por ejemplo, dado el conjunto ordenado {1,...,8} podemos expresar una permutación σ sobre éste mediante una matriz de correspondencias:
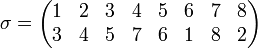
Claramente es biyectiva, ya que podemos encontrar una aplicación inversa σ − 1 de forma que su composición genera la aplicación identidad. Para ello, en primer lugar intercambiamos las filas y finalmente reordenamos las columnas de modo que los elementos del dominio queden ordenados de forma natural:

[editar] Notación de ciclos
Existe otra notación más compacta, llamada notación de ciclos. Un ciclo de longitud s es una permutación que intercambia cíclicamente s elementos y fija los restantes.
Esta notación revela mejor la estructura interna de la permutación. Para ello:
- Empezamos con cualquier elemento. Lo escribimos, a su derecha escribimos su imagen, a la derecha de esta, la imagen de su imagen, y seguimos así hasta que se complete un ciclo.
- Luego cogemos cualquier elemento no contenido en el primer ciclo, volvemos a escribir su imagen a su derecha, y continuamos hasta completar el segundo ciclo.
- El proceso continúa hasta que la permutación entera ha quedado descrita como producto de ciclos disjuntos.
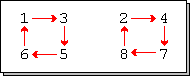
Siguiendo con el mismo ejemplo de antes, en notación de ciclos, σ quedaría expresada como composición de dos ciclos:
σ= (1 3 5 6 )(2 4 7 8)[editar] Descomposición de una permutación en ciclos disjuntos
La descomposición realizada por el procedimiento anterior no es única en principio, pues podrían haberse obtenido cualquiera de estos resultados equivalentes:
σ = (1 3 5 6)(2 4 7 8)=(2 4 7 8) (1 3 5 6)=(7 8 2 4)(6 1 3 5)La descomposición canónica de una permutación como producto de ciclos se obtiene colocando en primer lugar de cada ciclo el número más pequeño del mismo. Posteriormente se procede a la colocación de los ciclos, colocando primero el ciclo cuyo primer elemento sea menor. Frecuentemente, suelen omitirse los ciclos de longitud 1. Así la permutación (1 3)(2)(4 5) se escribe simplemente como (1 3)(4 5).
[editar] Descomposición de una permutación en trasposiciones
Una trasposición es una permutación que intercambia dos elementos y fija los restantes. Dicho de otro modo, es un ciclo de longitud 2. Una propiedad interesante es que cualquier permutación se puede construir como una composición de transposiciones, aunque no de manera única. Dadas dos descomposiciones en transposiciones de una permutación se cumple que ambas usaran un número par o ambas usarán un número impar, eso permite definir de manera unívoca la signatura de una permutación.
Las trasposiciones permiten descomponer una permutación cualquiera de una forma diferente a la descomposición en ciclos. En particular, las trasposiciones que aparezcan no tendrán que ser disjuntas: Por ejemplo, el ciclo (1 2 3 4) = (1 2) (2 3) (3 4). Aquí el orden de aplicación es importante: en primer lugar (3 4) deja el 4 en su sitio definitivo y el 3 descolocado. Después (2 3) deja en su sitio definitivo el 3 y el 2 descolocado, que quedará recolocado definitivamente por (1 2).
Para ver que cualquier permutación descompone como producto de trasposiciones bastará ver que todo ciclo lo hace. De hecho, la descomposición del ciclo de nuestro ejemplo se generaliza a la fórmula:
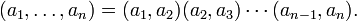
No habrá unicidad en la descomposición, ni siquiera en el número de trasposiciones necesarias. Pero se demuestra que si σ admite dos descomposiciones distintas con n y con m trasposiciones, entonces n y m tendrán la misma paridad (serán simultáneamente pares o impares). Dada una permutación cualquiera, se define el siguiente morfismo de grupos:
Donde 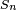 es el grupo simétrico de n elementos y m es un número entero, tal que exiten transposiciones
es el grupo simétrico de n elementos y m es un número entero, tal que exiten transposiciones 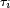 tales que:
tales que:
[editar] Permutación par y permutación impar
Llamaremos permutación par (resp. impar) a la que se escribe como composición de un número par (resp. impar) de trasposiciones.
Como ejemplo, de las 6=3! permutaciones del conjunto {1, 2, 3}, escritas en notación de ciclos:
- (1 2), (2 3) y (1 3) son, de forma trivial, impares.
- (1 2 3) y (1 3 2) son pares, como es fácil de comprobar al aplicar la fórmula anterior de descomposición de un ciclo en trasposiciones.
- e (la identidad) también es par.
En general, se demuestra que la mitad de las n! permutaciones de un conjunto de n elementos son pares y la otra mitad impares.
[editar] Estructura de grupo
Dado un número natural 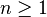 , consideramos el conjunto X = {1,2,...,n}. Definimos el grupo de permutaciones de n elementos, que denotaremos por Sn, o lo que es lo mismo, el conjunto de aplicaciones biyectivas de X a X.
, consideramos el conjunto X = {1,2,...,n}. Definimos el grupo de permutaciones de n elementos, que denotaremos por Sn, o lo que es lo mismo, el conjunto de aplicaciones biyectivas de X a X.
Las permutaciones pares forman un subgrupo normal de índice 2 del grupo Sn, al que llamaremos grupo alternado, y notaremos por An.
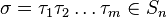
0 comentarios