MATEMÁTICAS3: INTERVALO. En Análisis matemático, se denomina intervalo a la máxima división sectorial sumisa, es decir a el subconjunto de la doble implicación latente en matemáticas subconjunto conexo de la recta real.
Intervalo (matemática)
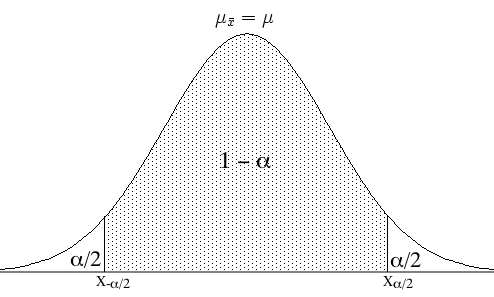
En Análisis matemático, se denomina intervalo a la máxima división sectorial sumisa, es decir a el subconjunto de la doble implicación latente en matemáticas subconjunto conexo de la recta real. Más precisamente, son las únicas partes I de R que verifican la siguiente propiedad:
|
Contenido[ocultar] |
[editar] Notación
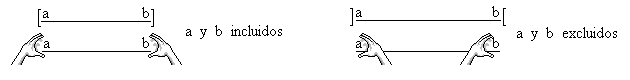
Es un conjunto de números que se corresponden con los puntos de una recta o segmento, en el que se encuentra un ordenamiento interno entre ellos. Los intervalos es el espacio que se da de un punto a otro en el cual se toman en cuenta todos los puntos intermedios. Por ejemplo: en una recta tenemos un intervalo:[-2,2]entre este espacio se encuentran los números (-2-1,0,1,2) aquí se encuentra un intervalo.....ya que el espacio abarca una serie de números consecutivos que se corresponden entre sí.
También existe una regla ERRONEA para el uso del paréntesis: si se dibuja sobre la recta real dos intervalos adyacentes, como (0; 1) y (1; 2) (es decir, se pinta la recta real y se coloca cuatro paréntesis donde corresponda), entre los dos intervalos cabe un signo 1 (o lo que corresponda según los intervalos) cabe, apretado pero cabe. Mientras que si los dos intervalos son (0, 1] y [1, 2), o (0, 1] y [1, 2) el número no cabe, o cabe muy estrangulado. O sea, que si los dos intervalos son abiertos, el número 1 no pertenece a ninguno, y por tanto hay espacio para meterlo en medio.
[editar] Clasificación
Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados y semi abiertos) o según sus características métricas (su longitud: nula, finita no nula, o infinita).
Aquí están todos los casos posibles, con a ≤ b, y x perteneciente al intervalo, y l su longitud:
| Notación | Intervalo | Longitud (l) | Descripción |
|---|---|---|---|
![[a, b] ,](https://petalofucsia.blogia.com/upload/externo-ce151b90f347ecc5032a66dfcc3dfd0d.png) | 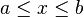 | 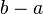 | Intervalo cerrado de longitud finita. |
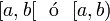 | 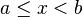 | 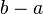 | Intervalo cerrado en a, abierto en b (semicerrado, semiabierto). |
![]a, b] mathrm{ acute o } (a, b] !](https://petalofucsia.blogia.com/upload/externo-4e73ba54e5f1ff3d874e1c869a9feb57.png) | 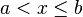 | 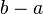 | intervalo abierto en a, cerrado en b. |
![]a, b[ mathrm{ acute o } (a, b) !](https://petalofucsia.blogia.com/upload/externo-0197e6f78ceb08b9c88a1f8e8761cc9b.png) | 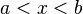 | 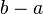 | intervalo abierto. |
![]-infty, b[ mathrm{ acute o } (- infty, b) !](https://petalofucsia.blogia.com/upload/externo-ac37a73a8ce88645fbd870088f5c4d8e.png) | 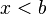 | 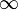 | Intervalo (semi) abierto. |
![]-infty, b] mathrm{ acute o } (- infty, b] !](https://petalofucsia.blogia.com/upload/externo-7c9cd3491ba55e5e7c32ee002fd5107d.png) | 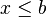 | 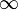 | Intervalo (semi) cerrado. |
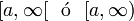 | 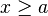 | 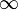 | Intervalo (semi) cerrado. |
![]a, infty [ mathrm{ acute o } (a, infty ) !](https://petalofucsia.blogia.com/upload/externo-83b88db0772c72eb8b011fe3af9c5239.png) | 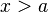 | 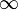 | Intervalo (semi) abierto. |
![]infty, + infty [ mathrm{ acute o } (infty, + infty ) !](https://petalofucsia.blogia.com/upload/externo-71bd273510c5e72bfca09cb657071b43.png) | 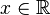 | 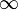 | Intervalo a la vez abierto y cerrado. |
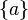 |  | 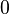 | intervalo cerrado de longitud nula. Es un conjunto unitario. |
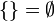 | x no existe | Sin longitud | conjunto vacío. |
Un intervalo abierto o cerrado (pero no semiabierto) de longitud finita se puede también definir a partir de su centro y de su radio:
Si I = ]a, b[, su centro es c = (a + b)/2, y su radio es r = (b - a)/2. a < x < b equivale a |x - c| < r; y se interpreta como la distancia entre x y c es menor que r; se nota x ε B (c, r); B para bola abierta, término que se generaliza a cualquier espacio métrico.
De la misma manera, I = [a, b] corresponde a la condición |x - c| ≤ r. En tal caso se habla de bola cerrada. Se nota este conjunto:
_
B (c, r) = { x ε R, |x - c| ≤ r }. Es la clausura topológica de la bola abierta B (c, r) = { x ε R, |x - c| < r }.
Cuando dos variables - pongamos x e y - toman sus valores en sendos intervalos I e J, es legítimo preguntarse en que intervalo varían su suma, su diferencia, su producto y su cociente. Contestar a esta pregunta permitirá definir las cuatro operaciones sobre los intervalos.
Tomemos I = [a, b] y J = [c, d]. Entonces a ≤ x ≤ b, y c ≤ y ≤ d.
podemos sumar las inegualdades: a + c ≤ x + y ≤ b + d. Lo que justifica que I + J = [ a + c , b + d ].
Para la diferencia, hay que mirar primero - y : - d ≤ - y ≤ - c, y luego se puede sumar las inegualdades: a - d ≤ x - y ≤ b - c. De ahí obtenemos I - J = [ a - d, b - c ].
Si se toman a, b, c y d positivos no nulos, el producto y el cociente son también sencillos: I · J = [ ac, bd ] y I / J = [ a/d, b/c ].
[editar] Generalización
Un entorno de centro a y radio δ es un conjunto de puntos cuya distancia a a es menor de δ. O sea:
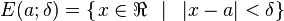
En particular si 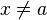 se denomina entorno reducido (E`).
se denomina entorno reducido (E`).
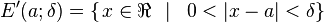 el cual no es un intervalo pues es un conjunto disconexo entonces se cambia la x por y o p
el cual no es un intervalo pues es un conjunto disconexo entonces se cambia la x por y o p
0 comentarios