MATEMÁTICAS2: SISTEMA BINARIO. ¿QUE PASA SI PONEMOS TODOS LOS NÚMEROS EN BASE DOS? ¿SE POTENCIAN?. Una serie completa de 8 trigramas y 64 hexagramas (análogos a 3 bit) y números binarios de 6 bit eran conocidos en la antigua China en el texto clásico del I Ching. Series similares de combinaciones binarias también han sido utilizadas en sistemas de adivinación tradicionales africanos, como el Ifá, así como en la geomancia medieval occidental. Un arreglo binario ordenado de los hexagramas del I Ching, representando la secuencia decimal de 0 a 63, y un método para generar el mismo fue desarrollado por el erudito y filósofo Chino Shao Yong en el siglo XI. Sin embargo, no hay ninguna prueba de que Shao entendiera el cómputo binario.
Sistema binario
El sistema binario, en matemáticas e informática, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Es el que se utiliza en las computadoras, pues trabajan internamente con dos niveles de voltaje, por lo que su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).
[editar] Historia del sistema binario
El antiguo matemático indio Pingala presentó la primera descripción que se conoce de un sistema de numeración binario en el siglo III a. C.
Una serie completa de 8 trigramas y 64 hexagramas (análogos a 3 bit) y números binarios de 6 bit eran conocidos en la antigua China en el texto clásico del I Ching. Series similares de combinaciones binarias también han sido utilizadas en sistemas de adivinación tradicionales africanos, como el Ifá, así como en la geomancia medieval occidental.
Un arreglo binario ordenado de los hexagramas del I Ching, representando la secuencia decimal de 0 a 63, y un método para generar el mismo fue desarrollado por el erudito y filósofo Chino Shao Yong en el siglo XI. Sin embargo, no hay ninguna prueba de que Shao entendiera el cómputo binario.
En 1605 Francis Bacon habló de un sistema por el cual las letras del alfabeto podrían reducirse a secuencias de dígitos binarios, las cuales podrían ser codificadas como variaciones apenas visibles en la fuente de cualquier texto arbitrario.
El sistema binario moderno fue documentado en su totalidad por Leibniz, en el siglo XII, en su artículo "Explication de l'Arithmétique Binaire". En él se mencionan los símbolos binarios usados por matemáticos chinos. Leibniz utilizó el 0 y el 1, al igual que el sistema de numeración binario actual.
En 1854, el matemático británico George Boole publicó un artículo que marcó un antes y un después, detallando un sistema de lógica que terminaría denominándose Álgebra de Boole. Dicho sistema desempeñaría un papel fundamental en el desarrollo del sistema binario actual, particularmente en el desarrollo de circuitos electrónicos.
[editar] Aplicaciones
En 1937, Claude Shannon realizó su tesis doctoral en el MIT, en la cual implementaba el Álgebra de Boole y aritmética binaria utilizando relés y conmutadores por primera vez en la historia. Titulada Un Análisis Simbólico de Circuitos Conmutadores y Relés, la tesis de Shannon básicamente fundó el diseño práctico de circuitos digitales.
En noviembre de 1937, George Stibitz, trabajando por aquel entonces en los Laboratorios Bell, construyó una computadora basada en relés —a la cual apodó "Modelo K" (porque la construyó en una cocina, en inglés "kitchen")— que utilizaba la suma binaria para realizar los cálculos. Los Laboratorios Bell autorizaron un completo programa de investigación a finales de 1938, con Stibitz al mando. El 8 de enero de 1940 terminaron el diseño de una "Calculadora de Números Complejos", la cual era capaz de realizar cálculos con números complejos. En una demostración en la conferencia de la Sociedad Americana de Matemáticas, el 11 de septiembre de 1940, Stibitz logró enviar comandos de manera remota a la Calculadora de Números Complejos a través de la línea telefónica mediante un teletipo. Fue la primera máquina computadora utilizada de manera remota a través de la línea de teléfono. Algunos participantes de la conferencia que presenciaron la demostración fueron John Von Neumann, John Mauchly y Norbert Wiener, quien escribió acerca de dicho suceso en sus diferentes tipos de memorias en la cual alcanzó diferentes logros.
[editar] Representación
Un número binario puede ser representado por cualquier secuencia de bits (dígitos binarios), que suelen representar cualquier mecanismo capaz de estar en dos estados mutuamente excluyentes. Las siguientes secuencias de símbolos podrían ser interpretadas como el mismo valor numérico binario:
1 0 1 0 0 1 1 0 1 0
| - | - - | | - | -
x o x o o x x o x o
y n y n n y y n y n
El valor numérico representado en cada caso depende del valor asignado a cada símbolo. En una computadora, los valores numéricos pueden representar dos voltajes diferentes; también pueden indicar polaridades magnéticas sobre un disco magnético. Un "positivo", "sí", o "sobre el estado" no es necesariamente el equivalente al valor numérico de uno; esto depende de la nomenclatura usada.
De acuerdo con la representación más habitual, que es usando números árabes, los números binarios comúnmente son escritos usando los símbolos 0 y 1. Los números binarios se escriben a menudo con subíndices, prefijos o sufijos para indicar su base. Las notaciones siguientes son equivalentes:
- 100101 binario (declaración explícita de formato)
- 100101b (un sufijo que indica formato binario)
- 100101B (un sufijo que indica formato binario)
- bin 100101 (un prefijo que indica formato binario)
- 1001012 (un subíndice que indica base 2 (binaria) notación)
- %100101 (un prefijo que indica formato binario)
- 0b100101 (un prefijo que indica formato binario, común en lenguajes de programación)
[editar] Conversión entre binario y decimal
[editar] Decimal a binario
Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente. Ordenados los restos, del último al primero, éste será el número binario que buscamos.
EjemploTransformar el número decimal 131 en binario. El método es muy simple:131 dividido entre 2 da 65 y el resto es igual a 1
65 dividido entre 2 da 32 y el resto es igual a 1
32 dividido entre 2 da 16 y el resto es igual a 0
16 dividido entre 2 da 8 y el resto es igual a 0
8 dividido entre 2 da 4 y el resto es igual a 0
4 dividido entre 2 da 2 y el resto es igual a 0
2 dividido entre 2 da 1 y el resto es igual a 0
-> Ordenamos los restos, teniendo en cuenta que el último valor de la division es menor de 2 y empezamos por ese resultado al primero de los restos: 10000011
En sistema binario, 131 se escribe 10000011
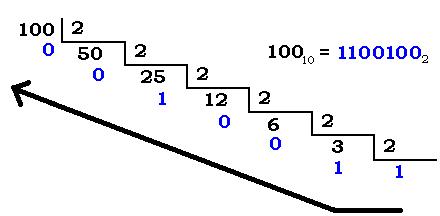
EjemploTransformar el número decimal 100 en binario.Otra forma de conversión consiste en un método parecido a la factorización en números primos. Es relativamente fácil dividir cualquier número entre 2. Este método consiste también en divisiones sucesivas. Dependiendo de si el número es par o impar, colocaremos un cero o un uno en la columna de la derecha. Si es impar, le restaremos uno y seguiremos dividiendo entre dos, hasta llegar a 1. Después sólo nos queda tomar el último resultado de la columna izquierda (que siempre será 1) y todos los de la columna de la derecha y ordenar los dígitos de abajo a arriba.
Ejemplo100|0
50|0
25|1 --> 1, 25-1=24 y seguimos dividiendo por 2
12|0
6|0
3|1
1|1 --> (100)10 = (1100100)2
Existe un último método denominado de distribución. Consiste en distribuir los unos necesarios entre las potencias sucesivas de 2 de modo que su suma resulte ser el número decimal a convertir. Sea por ejemplo el número 151, para el que se necesitarán las 8 primeras potencias de 2, ya que la siguiente, 28=256, es superior al número a convertir. Se comienza poniendo un 1 en 128, por lo que aún faltarán 23, 151 - 128 = 23, para llegar al 151. Este valor se conseguirá distribuyendo unos entre las potencias cuya suma dé el resultado buscado y poniendo ceros en el resto. En el ejemplo resultan ser las potencias 4, 2, 1 y 0, esto es, 16, 4, 2 y 1, respectivamente.
Ejemplo20= 1|1
21= 2|1
22= 4|1
23= 8|0
24= 16|1
25= 32|0
26= 64|0
27= 128|1 128 + 16 + 4 + 2 + 1 = (151)10 = (10010111)2
[editar] Decimal (con decimales) a binario
Para transformar un número del sistema decimal al sistema binario:
- Se transforma la parte entera a binario. (Si la parte entera es 0 en binario será 0, si la parte entera es 1 en binario será 1, si la parte entera es 5 en binario será 101 y así sucesivamente).
- Se sigue con la parte fraccionaria, multiplicando cada número por 2. Si el resultado obtenido es mayor o igual a 1 se anota como un uno (1) binario. Si es menor que 1 se anota como un 0 binario. (Por ejemplo, al multiplicar 0.6 por 2 obtenemos como resultado 1.2 lo cual indica que nuestro resultado es un uno (1) en binario, solo se toma la parte entera del resultado).
- Después de realizar cada multiplicación, se colocan los números obtenidos en el orden de su obtención.
- Algunos números se transforman en dígitos periódicos, por ejemplo: el 0.1.
Ejemplo
0,3125 (decimal) => 0,0101 (binario).Ejemplo
Proceso:
0,3125 · 2 = 0,625 => 0
0,625 · 2 = 1,25 => 1
0,25 · 2 = 0,5 => 0
0,5 · 2 = 1 => 1
En orden: 0101 -> 0,0101 (binario)
0,1 (decimal) => 0,0 0011 0011 ... (binario).Ejemplo
Proceso:
0,1 · 2 = 0,2 ==> 0
0,2 · 2 = 0,4 ==> 0
0,4 · 2 = 0,8 ==> 0
0,8 · 2 = 1,6 ==> 1
0,6 · 2 = 1,2 ==> 1
0,2 · 2 = 0,4 ==> 0 <--se repiten las cuatro cifras, periódicamente
0,4 · 2 = 0,8 ==> 0 <-
0,8 · 2 = 1,6 ==> 1 <-
0,6 · 2 = 1,2 ==> 1 <- ...
En orden: 0 0011 0011 ... => 0,0 0011 0011 ... (binario periódico)
5.5 = 5,5Ejemplo
5,5 (decimal) => 101,1 (binario).
Proceso:
5 => 101
0,5 · 2 = 1 => 1
En orden: 1 (un sólo digito fraccionario) -> 101,1 (binario)
6,83 (decimal) => 110,110101000111 (binario).
Proceso:
6 => 110
0,83 · 2 = 1,66 => 1
0,66 · 2 = 1,32 => 1
0,32 · 2 = 0,64 => 0
0,64 · 2 = 1,28 => 1
0,28 · 2 = 0,56 => 0
0,56 · 2 = 1,12 => 1
0,12 · 2 = 0,24 => 0
0,24 · 2 = 0,48 => 0
0,48 · 2 = 0,96 => 0
0,96 · 2 = 1,92 => 1
0,92 · 2 = 1,84 => 1
0,84 · 2 = 1,68 => 1
En orden: 110101000111 (binario)
Parte entera: 110 (binario)
Encadenando parte entera y fraccionaria: 110,110101000111 (binario)
[editar] Binario a decimal
Para realizar la conversión de binario a decimal, realice lo siguiente:
- Inicie por el lado derecho del número en binario, cada cifra multiplíquela por 2 elevado a la potencia consecutiva (comenzando por la potencia 0, 20).
- Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.
Ejemplos:
- (Los números de arriba indican la potencia a la que hay que elevar 2)
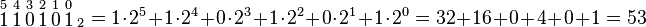
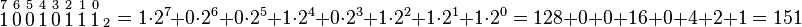
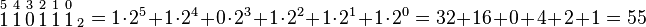
También se puede optar por utilizar los valores que presenta cada posición del número binario a ser transformado, comenzando de derecha a izquierda, y sumando los valores de las posiciones que tienen un 1.
EjemploEl número binario 1010010 corresponde en decimal al 82. Se puede representar de la siguiente manera:
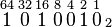
entonces se suman los números 64, 16 y 2:
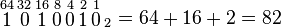
Para cambiar de binario con decimales a decimal se hace exactamente igual, salvo que la posición cero (en la que el dos es elevado a la cero) es la que está a la izquierda de la coma y se cuenta hacia la derecha a partir de -1:
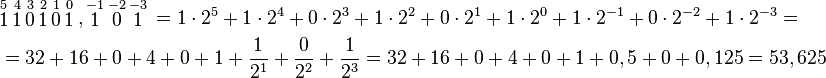
[editar] Binario a decimal (con parte fraccionaria binaria)
1. Inicie por el lado izquierdo (la primera cifra a la derecha de la coma), cada número multiplíquelo por 2 elevado a la potencia consecutiva a la inversa (comenzando por la potencia -1, 2-1).
2.Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.
Ejemplos- 0,101001 (binario) = 0,640625(decimal). Proceso:
1 · 2 elevado a -1 = 0,5
0 · 2 elevado a -2 = 0
1 · 2 elevado a -3 = 0,125
0 · 2 elevado a -4 = 0
0 · 2 elevado a -5 = 0
1 · 2 elevado a -6 = 0,015625
La suma es: 0,640625
- 0.110111 (binario) = 0,859375(decimal). Proceso:
1 · 2 elevado a -1 = 0,5
1 · 2 elevado a -2 = 0,25
0 · 2 elevado a -3 = 0
1 · 2 elevado a -4 = 0,0625
1 · 2 elevado a -5 = 0,03125
1 · 2 elevado a -6 = 0,015625
La suma es: 0,859375
[editar] Operaciones con números binarios
[editar] Suma de números binarios
La tabla de sumar para números binarios es la siguiente:
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10 |
Las posibles combinaciones al sumar dos bits son:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10
Note que al sumar 1 + 1 es 102, es decir, llevamos 1 a la siguiente posición de la izquierda (acarreo). Esto es equivalente, en el sistema decimal a sumar 9 + 1, que da 10: cero en la posición que estamos sumando y un 1 de acarreo a la siguiente posición.
Ejemplo1
10011000
+ 00010101
———————————
10101101
Se puede convertir la operación binaria en una operación decimal, resolver la decimal, y después transformar el resultado en un (número) binario. Operamos como en el sistema decimal: comenzamos a sumar desde la derecha, en nuestro ejemplo, 1 + 1 = 10, entonces escribimos 0 en la fila del resultado y llevamos 1 (este "1" se llama acarreo o arrastre). A continuación se suma el acarreo a la siguiente columna: 1 + 0 + 0 = 1, y seguimos hasta terminar todas la columnas (exactamente como en decimal).
[editar] Resta de números binarios
El algoritmo de la resta en sistema binario es el mismo que en el sistema decimal. Pero conviene repasar la operación de restar en decimal para comprender la operación binaria, que es más sencilla. Los términos que intervienen en la resta se llaman minuendo, sustraendo y diferencia.
Las restas básicas 0 - 0, 1 - 0 y 1 - 1 son evidentes:
- 0 - 0 = 0
- 1 - 0 = 1
- 1 - 1 = 0
- 0 - 1 = 1 (se transforma en 10 - 1 = 1) (en sistema decimal equivale a 2 - 1 = 1)
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 0 - 1 = 1 y me llevo 1, lo que equivale a decir en el sistema decimal, 2 - 1 = 1.
Ejemplos10001 11011001
-01010 -10101011
—————— —————————
00111 00101110
En sistema decimal sería: 17 - 10 = 7 y 217 - 171 = 46.
Para simplificar las restas y reducir la posibilidad de cometer errores hay varios métodos:
- Dividir los números largos en grupos. En el siguiente ejemplo, vemos cómo se divide una resta larga en tres restas cortas:
100110011101 1001 1001 1101
-010101110010 -0101 -0111 -0010
————————————— = ————— ————— —————
010000101011 0100 0010 1011
- Utilizando el complemento a dos (C2). La resta de dos números binarios puede obtenerse sumando al minuendo el «complemento a dos» del sustraendo.
La siguiente resta, 91 - 46 = 45, en binario es:
1011011 1011011
-0101110 el C2 de 0101110 es 1010010 +1010010
———————— ————————
0101101 10101101
En el resultado nos sobra un bit, que se desborda por la izquierda. Pero, como el número resultante no puede ser más largo que el minuendo, el bit sobrante se desprecia.
Un último ejemplo: vamos a restar 219 - 23 = 196, directamente y utilizando el complemento a dos:
11011011 11011011
-00010111 el C2 de 00010111 es 11101001 +11101001
————————— —————————
11000100 111000100
Y, despreciando el bit que se desborda por la izquierda, llegamos al resultado correcto: 11000100 en binario, 196 en decimal.
- Utilizando el complemento a uno. La resta de dos números binarios puede obtenerse sumando al minuendo el complemento a uno del sustraendo y a su vez sumarle el bit que se desborda.
[editar] Producto de números binarios
La tabla de multiplicar para números binarios es la siguiente:
| · | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
El algoritmo del producto en binario es igual que en números decimales; aunque se lleva a cabo con más sencillez, ya que el 0 multiplicado por cualquier número da 0, y el 1 es el elemento neutro del producto.
Por ejemplo, multipliquemos 10110 por 1001:
10110
1001
—————————
10110
00000
00000
10110
—————————
11000110
En sistemas electrónicos, donde suelen usarse números mayores, se utiliza el método llamado algoritmo de Booth.
11101111
111011
__________
11101111
11101111
00000000
11101111
11101111
11101111
______________
11011100010101
[editar] División de números binarios
La división en binario es similar a la decimal; la única diferencia es que a la hora de hacer las restas, dentro de la división, éstas deben ser realizadas en binario.
EjemploDividir 100010010 (274) entre 1101 (13):
100010010 |1101
——————
-0000 010101
———————
10001
-1101
———————
01000
- 0000
———————
10000
- 1101
———————
00011
- 0000
———————
01110
- 1101
———————
00001
[editar] Conversión entre binario y octal
[editar] Binario a octal
Para realizar la conversión de binario a octal, realice lo siguiente:
1) Agrupe la cantidad binaria en grupos de 3 en 3 iniciando por el lado derecho. Si al terminar de agrupar no completa 3 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
| Número en binario | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Número en octal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
3) La cantidad correspondiente en octal se agrupa de izquierda a derecha.
Ejemplos- 110111 (binario) = 67 (octal). Proceso:
111 = 7
110 = 6
Agrupe de izquierda a derecha: 67
- 11001111 (binario) = 317 (octal). Proceso:
111 = 7
001 = 1
11 entonces agregue un cero, con lo que se obtiene 011 = 3
Agrupe de izquierda a derecha: 317
- 1000011 (binario) = 103 (octal). Proceso:
011 = 3
000 = 0
1 entonces agregue 001 = 1
Agrupe de izquierda a derecha: 103
[editar] Octal a binario
Cada dígito octal se convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.
Ejemplo- 247 (octal) = 010100111 (binario). El 2 en binario es 10, pero en binario de 3 bits es Oc(2) = B(010); el Oc(4) = B(100) y el Oc(7) = (111), luego el número en binario será 010100111.
[editar] Conversión entre binario y hexadecimal
[editar] Binario a hexadecimal
Para realizar la conversión de binario a hexadecimal, realice lo siguiente:
1) Agrupe la cantidad binaria en grupos de 4 en 4 iniciando por el lado derecho. Si al terminar de agrupar no completa 4 dígitos, entonces agregue ceros a la izquierda.
2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
| Número en binario | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Número en hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
3) La cantidad correspondiente en hexadecimal se agrupa de derecha a izquierda.
Ejemplos- 110111010 (binario) = 1BA (hexadecimal). Proceso:
1010 = A
1011 = B
1 entonces agregue 0001 = 1
Agrupe de derecha a izquierda: 1BA
- 11011110101 (binario) = 6F5 (hexadecimal). Proceso:
0101 = 5
1111 = F
110 entonces agregue 0110 = 6
Agrupe de derecha a izquierda: 6F5
[editar] Hexadecimal a binario
Note que para pasar de Hexadecimal a binario, sólo que se remplaza por el equivalente de 4 bits, de forma similar a como se hace de octal a binario.
[editar] Tabla de conversión entre decimal, binario, hexadecimal, octal, BCD, Exceso 3 y Código Gray o Reflejado
| Decimal | Binario | Hexadecimal | Octal | BCD | Exceso 3 | Gray o Reflejado |
|---|---|---|---|---|---|---|
| 0 | 0000 | 0 | 0 | 0000 | 0011 | 0000 |
| 1 | 0001 | 1 | 1 | 0001 | 0100 | 0001 |
| 2 | 0010 | 2 | 2 | 0010 | 0101 | 0011 |
| 3 | 0011 | 3 | 3 | 0011 | 0110 | 0010 |
| 4 | 0100 | 4 | 4 | 0100 | 0111 | 0110 |
| 5 | 0101 | 5 | 5 | 0101 | 1000 | 0111 |
| 6 | 0110 | 6 | 6 | 0110 | 1001 | 0101 |
| 7 | 0111 | 7 | 7 | 0111 | 1010 | 0100 |
| 8 | 1000 | 8 | 10 | 1000 | 1011 | 1100 |
| 9 | 1001 | 9 | 11 | 1001 | 1100 | 1101 |
| 10 | 1010 | A | 12 | 0001 0000 | 1111 | |
| 11 | 1011 | B | 13 | 0001 0001 | 1110 | |
| 12 | 1100 | C | 14 | 0001 0010 | 1010 | |
| 13 | 1101 | D | 15 | 0001 0011 | 1011 | |
| 14 | 1110 | E | 16 | 0001 0100 | 1001 | |
| 15 | 1111 | F | 17 | 0001 0101 | 1000 |


0 comentarios