HISTORIA9: NÚMEROS INFINITOS. MATEMÁTICAS. El concepto de infinito aparece en varias ramas de la filosofía,[1] la matemática y la astronomía.[2] En geometría, el punto al infinito en geometría proyectiva y el punto de fuga en geometría descriptiva; en análisis matemático, los límites infinitos, o límites al infinito; y en matemática dentro de las teorías de números y de conjuntos. En todos los casos denota que el ente en cuestión no es finito en algún aspecto.
Infinito

El concepto de infinito aparece en varias ramas de la filosofía,[1] la matemática y la astronomía.[2] En geometría, el punto al infinito en geometría proyectiva y el punto de fuga en geometría descriptiva; en análisis matemático, los límites infinitos, o límites al infinito; y en matemática dentro de las teorías de números y de conjuntos. En todos los casos denota que el ente en cuestión no es finito en algún aspecto.
Contenido[ocultar] |
[editar] El símbolo de infinito

Los orígenes del símbolo de infinito 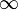 son inciertos. Dado que la forma se asemeja a la curva lemniscata (del latín lemniscus, es decir cinta), se ha sugerido que representa un lazo cerrado.
son inciertos. Dado que la forma se asemeja a la curva lemniscata (del latín lemniscus, es decir cinta), se ha sugerido que representa un lazo cerrado.
También se cree posible que la forma provenga de otros símbolos alquímicos o religiosos, como por ejemplo ciertas representaciones de la serpiente uróboros. El matemático John Wallis fue el primero en usar el símbolo 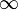 para representar al infinito en su tratado De sectionibus conicus en 1655.
para representar al infinito en su tratado De sectionibus conicus en 1655.
Se ha querido ver también una banda de Möbius en su forma, aunque el símbolo se usó durante cientos de años antes de que August Möbius descubriera la banda que lleva su nombre.
El símbolo de infinito se representa en Unicode con el carácter ∞ (U+221E).
[editar] Teoría de conjuntos
Los conjuntos finitos tienen una propiedad "intuitiva" que los caracteriza; dada una parte propia de los mismos, ésta contiene un número de elementos menor que todo el conjunto. Es decir, no puede establecerse una biyección entre una parte propia del conjunto finito y todo el conjunto. Sin embargo, esa propiedad "intuitiva" de los conjuntos finitos no la tienen los conjuntos infinitos, y formalmente decimos que:
Un conjunto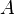 es infinito si existe un subconjunto propio
es infinito si existe un subconjunto propio 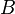 de
de 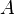 , es decir, un subconjunto
, es decir, un subconjunto 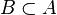 tal que
tal que 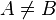 , tal que existe una biyección
, tal que existe una biyección 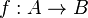 entre
entre 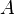 y
y 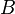 .
.La idea de cardinalidad de un conjunto se basa en la noción anterior de biyección. De dos conjuntos entre los que se puede establecer una biyección se dice que tienen la misma cardinalidad. Para un conjunto finito su cardinalidad puede representarse por un número natural. Por ejemplo, el conjunto {manzana, pera, durazno} tiene 3 elementos. Esto significa de modo más formal que se puede establecer una biyección entre tal conjunto y el conjunto {1,2,3}:

Dicho de otra forma, es posible hacer parejas (1, manzana), (2, pera), (3, durazno) de modo que cada elemento de los dos conjuntos se utilice exactamente una vez. Cuando es posible establecer tal relación "uno a uno" entre dos conjuntos se dice que ambos conjuntos tienen la misma cardinalidad, lo cual, para conjuntos finitos, equivale a que tengan el mismo número de elementos.
[editar] Primera definición positiva de conjunto infinito
La primera definición positiva de conjunto infinito fue dada por Georg Cantor y se basa en la siguiente observación: Si un conjunto S es finito y T es un subconjunto propio, no es posible construir una biyección entre S y T. Por ejemplo, si S = {1,2,3,4,5,6,7,8} y T = {2,4,6,8} no es posible construir una biyección entre S y T, porque de ser así tendrían la misma cardinalidad (el mismo número de elementos).
Un conjunto es infinito si es posible encontrar un subconjunto propio del mismo que tenga la misma cardinalidad que el conjunto original. Consideremos el conjunto de los números naturales N={1,2,3,4,5,...}, el cual es un conjunto infinito. Para verificar tal afirmación es necesario encontrar un subconjunto propio y construir una biyección entre ambos. Para este caso, consideremos el conjunto de enteros positivos pares P={2,4,6,8,10,...}. El conjunto P es un subconjunto propio de N, y la regla de asignación 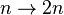 es una biyección:
es una biyección:
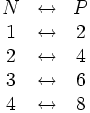
ya que a todo elemento de N le corresponde un único elemento de P y viceversa.
[editar] Números ordinales infinitos
Los números ordinales sirven para notar una posición en un conjunto ordenado (primer, segundo, tercer elemento ...). El ejemplo más elemental es el de los números naturales, que se definen rigurosamente así: Se nota 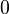 el conjunto vacío:
el conjunto vacío:
se nota 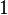 el conjunto que sólo contiene
el conjunto que sólo contiene 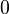 :
:
luego se nota 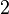 el conjunto que sólo contiene
el conjunto que sólo contiene 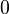 y
y 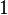 :
:
Y así sucesivamente:
Por construcción, 0 está incluido en 1, quién a su vez está incluido en 2, ya que obviamente:
La inclusión permite convertir a los ordinales en un conjunto bien ordenado (dos elementos distintos siempre se pueden comparar, y añadiendo la igualdad daría un orden total) entre estos conjuntos que se prefiere, por costumbre, escribir "<", lo que da las relaciones 0 < 1 < 2 < 3. Decir que un ordinal es menor (estrictamente) que otro significa, cuando se les considera a ambos como conjuntos, que está incluido en el otro.
Si a y b son ordinales, entonces aUb, la unión de los conjuntos, también es un ordinal. En particular, si son ordinales finitos (conjuntos finitos) correspondientes a los naturales a y b, entonces aUb corresponde al mayor de los dos, a o b. En general, si los conjuntos ai son ordinales, donde i toma todos los valores de un conjunto I, entonces a = Uai también lo será. Y si el conjunto I no es finito, tampoco lo será a. Así obtendremos ordinales (o sea números) infinitos.
Acabamos de caer en una "trampa", al hablar de conjunto finito sin definir el concepto. Para definirlo rigurosamente, debemos compararlo con los ordinales. Dos conjuntos bien ordenados A y B son isomorfos (con relación al orden) si existe una biyección f entre ambos que respeta el orden: si a < a' en A, entonces f(a) < f(a) en B. Resulta obvio constatar que si A es un conjunto ordenado con n elementos (n entero natural) entonces A es isomorfo an = {0, 1, 2, ..., n-1}. Basta con renombrar cada elemento de A para obtener A = {a0, a1, a2, ..., an-1}. Un isomorfismo es meramente un cambio de apelación. Diremos que un ordinal es finito si cada una de sus partes no vacías tiene un elemento máximo. Por lo tanto todo natural es un ordenal finito. La intuición nos dice que no hay otros ordenales finitos. Lógicamente, diremos que un conjunto ordenado es finito si es isomorfo a un ordinal finito, o sea a un natural.
Para introducir los ordinales infinitos, es preciso dar ahora la definición exacta de un ordinal:
Un conjunto A totalmente ordenado (por la inclusión) es un ordinal si y sólo si cada elemento de A es también un subconjunto de AYa vimos que es el caso para los naturales: Por ejemplo, el conjunto 2 = {0, 1} admite 1= {0}, como elemento y por lo tanto también como subconjunto.
Todo conjunto bien ordenado es isomorfo a un ordinal. Esto es obvio en el caso finito, y se muestra por inducción transfinita que lo es en el caso infinito. O sea, renombrando los elementos de un conjunto bien ordenado siempre obtenemos un ordinal.
[editar] Primer ordinal infinito
Ya hemos visto que una unión cualquiera de ordinales es un ordinal. Si tomamos una unión finita de ordinales finitos, fabricamos un ordinal finito. Para obtener el primer ordinal infinito tenemos que reunir un número no finito de ordinales finitos. Haciéndolo, siempre caemos en el mismo conjunto, construido al reunir todos los ordinales finitos, es decir los naturales. El conjunto de todos los naturales, ℕ, es pues el primer ordinal infinito, lo que no debería sorprender, y lo notamos en este contexto ω (omega).
Para visualizar los ordinales, resulta muy práctico representar cada uno por un punto de una sucesión creciente convergente, como por ejemplo un = 1 - 1/(n+1). Esto da algo semejante a:
X__________X_________X_______X______X______X_____X____X___X__X_X_XXX........Escojamos un punto de la sucesión, y miremos cuantos puntos están más a la izquierda. En el ejemplo, hay cuatro, y por lo tanto se trata de u4, lo que corresponde al ordinal 4. Para representar el ordinal w, resulta natural añadir a la sucesión previa un punto 'O' situado exactamente en el límite de la sucesión:
X__________X_________X_______X______X______X_____X____X___X__X_X_XXX...OA la izquierda de uw hay una infinidad de puntos, por lo tanto w es infinito. Pero si elegimos a cualquier otro punto de la sucesión a su izquierda, ya no es el caso, lo cual prueba que w es el primer ordinal infinito. Después de w llega w+1, w+2 ... que se representan añadiendo a la derecha uno dos o más puntos, inicialmente distantes, y luego más cercanos entre sí:
X________X________X_______X______X______X_____X____X___X__X_X_XXX...O_______X_____XEl último punto dibujado corresponde a w+2.
Más generalmente, para sumar dos ordinales A y B se cambian los nombres de los elementos para que sean todos distintos, luego se juntan los conjuntos A y B, poniendo B a la derecha de A es decir imponiendo que cada elemento de B sea mayor que todos los de A. Así hemos construido w+1, ... y así podemos construir 1+w: Notemos Y el elemento de 1, y X los de w:
Y__________X__________X_________X_______X______X______X_____X____X___X__X_X_XXX...Salta a la vista que w y 1+w son muy parecidos. De hecho la función x →x - 1 realiza un isomorfismo entre ellos (1+w tiene dos elementos llamados 0: 0A y 0B. El primero hace el papel de -1 en la función). Por lo tanto corresponden al mismo ordinal: 1+w = w. Mas no es el caso de w+1, que es distinto de w porque su el conjunto w+1 tiene un elemento máximo (el O del dibujo) mientras que el conjunto w no lo tiene (el límite de los naturales no es un natural).
El punto w (el O del dibujo) no tiene antecesor, es decir que no existe un n tal que n+1=w: se dice que w es un ordinal límite. Cero tiene también esta propiedad pero no merece esta apelación. Como w+1 ≠ 1+w, la adición no es conmutativa en los ordinales.
Se construye del mismo modo w + w que se nota lógicamente 2w. La multiplicación se define a partir de la adición como para los naturales.
Una vez que se ha representado nw, con n natural, no resulta demasiado difícil imaginar lo que será w.w, escrito w2. Luego se puede definir wn, con n natural, y, tomando el límite, ww, tiene tantos elementos como la recta real.
La sucesión wwww tiene como límite epsilon 0.
[editar] Números cardinales infinitos
El cardinal de un conjunto es el número de elementos que contiene. Esta noción es por lo tanto distinta del ordinal, que caracteriza el lugar de un elemento en una sucesión. "Cinco" difiere de "quinto" aunque obviamente existe una relación entre ambos.
Se dice que dos conjuntos tienen el mismo cardinal si existe una biyección entre ellos. Contrariamente a los ordinales, esta biyección no tiene que respetar el orden (además los conjuntos no tienen que ser ordenados).
Como ya tenemos un surtido de conjuntos -los ordinales- veamos sus tamaños (o sea sus cardinales) respectivos.
No es ninguna sorpresa que los ordinales finitos también son cardinales: entre dos conjuntos con n y m elementos, m y n distintos, no puede haber biyección, por lo tanto tienen cardinales distintos.
Pero no es el caso con los ordenales infinitos: Por ejemplo, w y w+1 están en biyección por la función:
w+1 → wx → x+1 y w → 0. Tal biyección no respeta el orden, por eso dos ordinales distintos pueden corresponder a un mismo cardinal.Se suele notar |A| el cardinal de A. Se llama 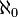 (alef0) el cardinal de w, o sea del conjunto de los naturales (donde alef es la primera letra del alfabeto hebreo).
(alef0) el cardinal de w, o sea del conjunto de los naturales (donde alef es la primera letra del alfabeto hebreo).
Si A y B son conjuntos, entonces |AxB| = |A|.|B|, donde x designa el producto cartesiano de los conjuntos, y "." es el producto de los cardinales definidos por esta fórmula. El conjunto de las partes de un conjunto A, P(A) está en biyección con el conjunto de las funciones de A hacia {0,1}, conjunto que de escribe 2A, como caso particular de YX que denota el conjunto de las aplicaciones de X hacia Y.
El cardinal de R, conjunto de los reales, es por lo tanto 2alef0, porque R está en biyección con las partes de N, por medio de la escritura decimal de los reales.
No se puede decidir, con los axiomas clásicos (los de la teoría de los conjuntos, fundamentos de la matemática), si existe un cardinal mayor que alef0 y menor que 2alef0, es decir si existe un conjunto con más elementos que N pero con menos elementos que R. La hipótesis del continuo, que es un axioma adicional, afirma que no.
[editar] Análisis matemático y topología
Otro significado común de infinito es, informalmente, cota superior para el conjunto de los números reales o infinito topológico, es decir, puede añadirse a los números reales un nuevo número 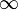 , que no sería un número real, pero tal que:
, que no sería un número real, pero tal que:
El conjunto de los números reales es un conjunto ordenado, es decir, dado una pareja de números es posible determinar el mayor y el menor. Por ejemplo, si a=2 y b=7 entonces a es el número menor y b es el mayor.
Un conjunto de números reales S es acotado superiormente si existe un número c (la cota) tal que c es mayor que todo elemento de S. Por ejemplo, si S={π ; 7 ; 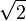 } entonces S es un conjunto acotado, ya que el número c=10 cumple que π<10, 7<10,
} entonces S es un conjunto acotado, ya que el número c=10 cumple que π<10, 7<10, 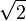 <10.
<10.
Cuando un conjunto no es acotado, para cualquier número c es posible encontrar 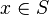 de modo que c < x. El concepto de infinito se introduce como una cota especial para este tipo de conjuntos. Este concepto de infinito se representa con el símbolo
de modo que c < x. El concepto de infinito se introduce como una cota especial para este tipo de conjuntos. Este concepto de infinito se representa con el símbolo 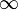 .
.
Consideremos nuevamente el conjunto de los números pares P={2,4,6,8,10,...}. El conjunto no es acotado, porque dado cualquier número c, existe un número par mayor a c. Por ejemplo, si c=100 entonces x=200 es mayor, si c=555 entonces x=1000 es mayor. También es posible decir que la sucesión ordenada de los números pares "tiende a infinito", o que su límite es infinito.
El Análisis matemático son las ramas de la matemática que estudian los límites y el infinito en este contexto.
En ocasiones se considera al infinito como un "número especial", agregando los símbolos 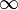 y
y 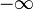 al conjunto de números reales
al conjunto de números reales 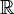 formando así el conjunto de números reales extendidos:
formando así el conjunto de números reales extendidos: 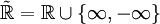 . Con esta construcción el infinito se manipula de manera similar a un número, sujeto a ciertas reglas:
. Con esta construcción el infinito se manipula de manera similar a un número, sujeto a ciertas reglas:
- Relación de orden:
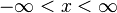 para cualquier número real
para cualquier número real 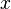 .
. - Operaciones aritméticas entre números reales y el infinito:
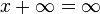 y
y 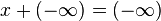
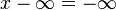
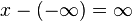
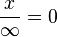 ,
, 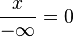 Si
Si 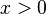 ,
, 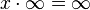 y
y 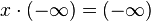 .Si
.Si 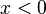 entonces
entonces 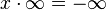 y
y 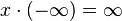 .
. - Operaciones aritméticas entre infinitos:
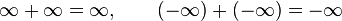
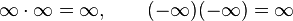
Nótese que muchas operaciones no están definidas (es decir, no tienen valor asignado), por ejemplo:
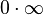
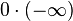
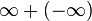
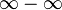
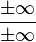
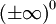
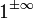
[editar] Infinito en informática
De manera relacionada con el infinito para números reales, algunos lenguajes de programación admiten un valor especial que recibe el nombre de infinito: valor que se puede obtener como resultado de ciertas operaciones matemáticas no realizables, tales como las descritas en el punto anterior u operaciones teóricamente posibles, pero demasiado complejas para su trabajo en el ordenador/lenguaje en cuestión. En otros lenguajes simplemente se produciría un error.
[editar] Véase también
[editar] Referencias
- ↑ Monnoyeur, Francoise (1995). El infinito de los matemáticos, el infinito de los filósofos (Infini des mathématiciens, infini des philosophes). Paris: Belin. ISBN 978-2701110189.
- ↑ Monnoyeur, Francoise (1999). El Infinito de los filósofos, el infinito de los astrónomos (Infini des philosophes, infini des astronomes). Paris: Belin. ISBN 978-2701115207.
[editar] Más información
- Manolios, Panagiotis & Vroon, Daron. Algorithms for ordinal arithmetic. Baader, Franz (ed), 19th International Conference on Automated Deduction--CADE-19. Pages 243-257 of LNAI, vol. 2741. Springer-Verlag.
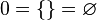
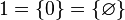
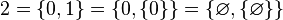
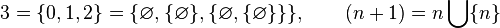

0 comentarios