MATEMÁTICAS: LÍMITES MATEMÁTICOS. LOS LÍMITES MATEMÁTICOS EXPLICAN CÓMO VARÍA UNAS SECUENCIA DE PUNTOS AL VARÍAR UNO DE ELLOS. TIENE MUCHAS APLICACIONES EN FÍSICA, ASTRONOMÍA Y ASTROLOGÍA Y EN CIENCIAS COMO LA GEOMETRÍA Y EL ANÁLISIS DIFERENCIAL O DE DIFERENCIAS. En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
Límite matemático
De Wikipedia, la enciclopedia libre
En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
Contenido[ocultar] |
Límite de una función [editar]
Definición rigurosa [editar]
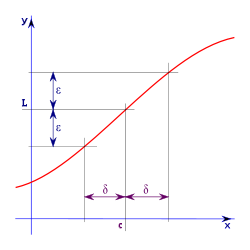
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:
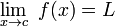
si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee. Formalmente, utilizando términos lógico-matemáticos:
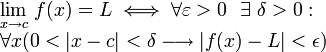
Esta definición se denomina frecuentemente definición épsilon-delta de límite, y se lee como:
Límites notables [editar]
Como ejemplo de límites notables tenemos los siguientes límites de funciones, que proveen resultados muy interesantes.
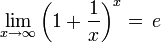 (número e)
(número e) 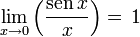
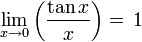
Demostración [editar]
Para demostrar, por ejemplo, el segundo de estos límites, se utilizará la inecuación sen(x) < x < tan(x) en el intervalo (0,π/2), que relaciona x con las funciones seno y tangente. Luego dividimos por sen(x), obteniendo:
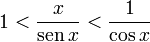
Invirtiendo los términos de la inecuación y cambiando los signos de desigualdad:
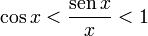
Calculando el límite cuando x tiende a 0:
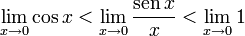
Lo que es igual a:
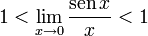
Aplicando el teorema del sándwich o teorema de estricción, el límite necesariamente vale 1:
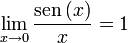
El tercero de los límites se demuestra utilizando las propiedades de los límites y el valor obtenido en el límite anterior. Es decir:
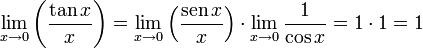
El límite que obtiene el número e se demuestra de manera análoga, desarrollando el binomio de Newton y aplicando el límite cuando x tiende a infinito.
Límite de una sucesión [editar]
La definición del límite matemático en el caso de una sucesión es muy parecida a la definición del límite de una función cuando x tiende a 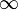 . Decimos que la sucesión an tiende hasta su límite a, o que converge o es convergente (a a), lo que denotamos como:
. Decimos que la sucesión an tiende hasta su límite a, o que converge o es convergente (a a), lo que denotamos como:
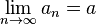
si podemos encontrar un número N tal que todos los términos de la sucesión a a cuando n crece sin cota. Formalmente:
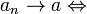
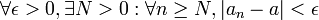
Propiedades de los límites [editar]
Generales [editar]
Los límites, como otros entes matemáticos, cumplen las siguientes propiedades generales, que son usadas muchas veces para simplificar el cálculo de los mismos.
- Límite por un escalar.
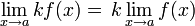 donde k es un multiplicador escalar.
donde k es un multiplicador escalar. - Límite de una suma.
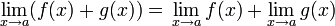
- Límite de una resta.
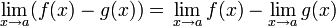
- Límite de una multiplicación.
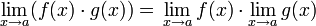
- Límite de una división.
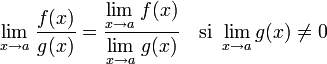
Indeterminaciones [editar]
Hay límites que evaluándolos directamente, se obtiene alguna de las siguientes expresiones:
A estas expresiones se les denomina indeterminaciones, ya que, a simple vista, no está claro cual puede ser el límite (si es que existe). Por ejemplo, en la segunda de estas ecuaciones, el límite pudiese valer 0, 1 o infinito. En algunos casos, simplificando las expresiones u obteniendo expresiones equivalentes a las iniciales, mediante racionalización o factorización se puede resolver la indeterminación y calcular el límite. En otros casos, se requerirá el uso de otras herramientas más potentes como pueden ser las desigualdades o la regla de L'Hopital.
Un ejemplo de indeterminación del tipo 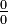 es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :
es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :
![lim_{trightarrow 0}frac{t}{t^2}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0}frac{1}{t} = infty](https://petalofucsia.blogia.com/upload/externo-2c2a8339dc5ed8ccd290f53129017bc9.png)
![lim_{trightarrow 0}frac{t}{t}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0} 1 =1](https://petalofucsia.blogia.com/upload/externo-c974cdd467d4b4aca64166c24df85228.png)
![lim_{trightarrow 0}frac{t^2}{t}=frac{0}{0} quad xrightarrow[mathrm{simplificando}]{} quad lim_{trightarrow 0} {t} = 0](https://petalofucsia.blogia.com/upload/externo-90fc66d0f750b2fd989ffd86b93fe625.png)

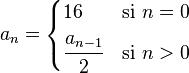
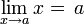
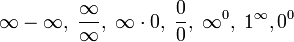
2 comentarios
petalofucsia -
Diccionario de la lengua española © 2005 Espasa-Calpe:
derivar
intr. y prnl. Tener origen o proceder de algo:
su maestría se deriva de una larga práctica.
mar. Desviarse el buque de su rumbo:
el bote derivó hacia el norte.
tr. Encaminar, conducir algo que va por un cauce para hacerlo ir por otro camino:
derivar un río hacia un embalse.
gram. Formar una palabra a partir de otra cambiando su forma:
"derechura" deriva de "derecho".
mat. Obtener una derivada.
Diccionario de la lengua española © 2005 Espasa-Calpe:
derivado, da
adj. y m. gram. [Palabra] que se forma por derivación:
ciertos sufijos solo forman derivados nominales.
m. quím. Producto que se obtiene de otro a través de una o varias transformaciones:
la gasolina es un derivado del petróleo.
f. mat. En las funciones matemáticas, límite hacia el cual tiende la razón entre el incremento de la función y el correspondiente a la variable, cuando este último tiende a cero:
la derivada expresa la variación de una función.
Preguntas en los foros con la(s) palabra(s) 'derivado' en el título:
ser/estar derivado
verbo derivado del sustantivo "neologismo"
Pregunta tú mismo.
Visita el foro.
'derivado' también aparece en estas entradas
ácido - alquilo - arilo - aristotelismo - artrosis - asturiano - bable - benzoico - butano - chachachá - derivada - descremado - evolucionismo - fenol - fuel - jazz - kerosén - lácteo - metilo - novocaína - octanol - opiáceo - patronímico - permanganato - procaína - soul - sulfito - sulfuro - trinitrotolueno - vinilo
petalofucsia -
En cálculo (rama de las matemáticas), la derivada representa cómo una función cambia a medida que su entrada cambia. En términos poco rigurosos, una derivada puede ser vista como cuánto está cambiando el valor de una cantidad en un punto dado; por ejemplo, la derivada de la posición de un vehículo con respecto al tiempo es la velocidad instantánea con la cual el vehículo está viajando.
La derivada de una función en un valor de entrada dado describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente en la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.