Blogia
petalofucsia

INGENIERÍA: VECTORES. Un vector es una magnitud física caracterizable mediante un módulo y una dirección u orientación, la cual puede ser representada en coordenadas polares o mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas. Alternativamente, de un modo más formal y abstracto, un vector es una magnitud física, que fijada una base, se representa por una secuencia de números o componentes independientes tales que sus valores sean relacionables de manera sistemática cuando son medidos por diferentes observadores.

- Ingeniería

Vector (física)

De Wikipedia, la enciclopedia libre

Para otros usos de este término, véase Vector.

Un vector es una magnitud física caracterizable mediante un módulo y una dirección u orientación, la cual puede ser representada en coordenadas polares o mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas. Alternativamente, de un modo más formal y abstracto, un vector es una magnitud física, que fijada una base, se representa por una secuencia de números o componentes independientes tales que sus valores sean relacionables de manera sistemática cuando son medidos por diferentes observadores.

Ejemplo

La distancia entre dos coches que parten de un mismo sitio no puede quedar determinada únicamente por sus celeridades, esto es, los módulos de sus velocidades. Si éstas son 30 y 40 km/h, al transcurrir una hora, la distancia entre los mismos podrá ser, entre otras posibilidades:

  • De 10 km, si los dos coches se mueven en la misma dirección.
  • De 70 km, si se mueven en dirección contraria.
  • De 50 km, si se mueven en direcciones perpendiculares.

Así, la distancia entre los dos coches, no depende sólo de la celeridad de los coches (lo que marca el velocímetro). Es necesario definir la velocidad con carácter vectorial, esto es, asociar dirección al dato numérico (o módulo).

Contenido

[ocultar]

Conceptos básicos [editar]

Esta sección explica los aspectos básicos, la necesidad de los vectores para representar ciertas magnitudes físicas, las componentes de un vector, la notación de los mismos, etc.

Magnitudes escalares y vectores [editar]

Representación gráfica de una magnitud vectorial, con indicación de su punto de aplicación y de los versores cartesianos.
Representación de los vectores

Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc., que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras que son llamadas escalares.

Las magnitudes escalares quedan representadas por el ente matemático más simple; por un número. Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, determinada por el ángulo que forma el vector con los ejes de coordenadas. Así pues, podemos enunciar:

Un vector es una magnitud física que tienen módulo y dirección.

Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el modulo del vector y la "punta de flecha" indica su dirección, la cual se mide en coordenadas polares.

Notación [editar]

Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flechita sobre la letra que designa su módulo (que es un escalar). Ejemplos:

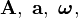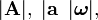  • mathbf A, mathbf a, boldsymbol{omega}, ... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector: |mathbf A|, |mathbf a, |boldsymbol{omega}|, ...
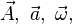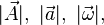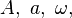  • En los textos manuscritos escribiríamos: vec A, vec a, vec{omega},... para los vectores y |vec A|, |vec a|, |vec {omega}|,... o A, a, {omega},... para los módulos.

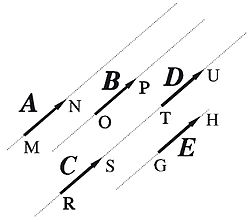
Cuando convenga, representaremos la magnitud vectorial haciendo referencia al origen y al extremo del segmento orientado que la representa geométricamente; así, designaremos los vectores representados en la Figura 2 en la forma 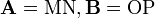mathbf A = text{MN}, mathbf B=text{OP} ,, ... resultando muy útil esta notación para los vectores desplazamiento.

Además de estas convenciones los vectores unitarios o versores, cuyo módulo es la unidad, se representan frecuentemente con un circunflejo encima, por ejemplo 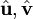hatmathbf{u}, hatmathbf{v}.

Tipos de vectores [editar]

Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse distintos tipos de los mismos:

  • Vectores libres: no están aplicados en ningún punto en particular.
  • Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
  • Vectores fijos o ligados: están aplicados en un punto en particular.

Podemos referirnos también a:

  • Vectores unitarios: vectores de módulo unidad.
  • Vectores concurrentes: sus rectas de acción concurren en un punto propio o impropio (paralelos).
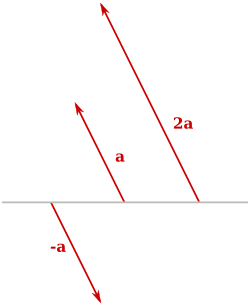
  • Vectores opuestos: vectores de igual magnitud, pero dirección contraria.
  • Vectores colineales: los vectores que comparten una misma recta de acción.
  • Vectores coplanarios: los vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).

Componentes de un vector [editar]

Componentes del vector

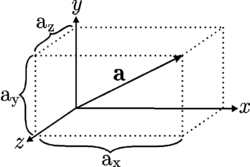
Un vector en el espacio se puede expresar como una combinación lineal de tres de vectores unitarios o versores perpendiculares entre sí que constituyen una base vectorial.

En coordenadas cartesianas, los vectores unitarios se representan por 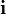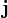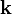mathbf{i} ,, mathbf{j} , mathbf{k} , paralelos a los ejes de coordenadas x, y, z positivos. Las componentes del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:

mathbf{a} = (a_x,a_y,a_z)

o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será

mathbf{a} = a_x , mathbf{i}+ a_y , mathbf{j} + a_z , mathbf{k}

Estas representaciones son equivalentes entre sí, y los valores ax, ay, az, son las componentes vector que, salvo que se indique lo contrario, son números reales.

Operaciones con vectores [editar]

Suma de vectores [editar]

Para sumar dos vectores libres vector y vector se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Método del paralelogramo
Método del triángulo

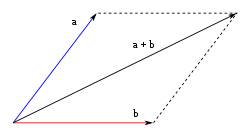
Método del paralelogramo [editar]

Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, completando un paralelogramo trazando rectas paralelas a cada uno de los vectores, en el extremo del otro (ver gráfico a la derecha). El resultado de la suma es la diagonal del paralelogramo que parte del origen común de ambos vectores.

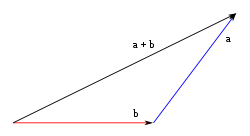
Método del triángulo [editar]

Consiste en disponer gráficamente un vector a continuación de otro; es decir, el origen de uno de los vectores se lleva sobre el extremo del otro. A continuación se une el origen del primer vector con el extremo del segundo.

Método analítico. Suma y diferencia de vectores [editar]

Dados dos vectores libres,

mathbf{a} = (a_x mathbf{i} + a_y mathbf{j} + a_z mathbf{k})

mathbf{b} = (b_x mathbf{i} + b_y mathbf{j} + b_z mathbf{k})

El resultado de su suma o de su diferencia se expresa en la forma

mathbf{a} pm mathbf{b} = (a_x mathbf{i} +a_y mathbf{j} +a_z mathbf{k}) pm (b_x mathbf{i} +b_y mathbf{j} +b_z mathbf{k})

y ordenando las componentes,

mathbf{a} pm mathbf{b} = (a_x + b_x) mathbf{i} + (a_y + b_y) mathbf{j} + (a_z + b_z)mathbf{k}

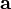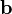Conocidos los módulos de dos vectores dados, mathbf{a} y mathbf{b}, así como el ángulo θ que forman entre sí, el módulo de 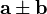mathbf{a} pm mathbf{b} es:

|mathbf{a} pm mathbf{b}| = sqrt{a^2 + b^2 + 2ab cos theta}

La deducción de esta expresión puede consultarse en deducción del módulo de la suma.

Producto de un vector por un escalar [editar]

Producto por un escalar

El producto de un vector por un escalar es otro vector cuyo módulo es el producto del escalar por el módulo del vector, cuya dirección es igual a la del vector, o contraria a este si el escalar es negativo.

Partiendo de la representación gráfica del vector, sobre la misma línea de su dirección tomamos tantas veces el módulo de vector como marque el escalar.

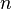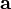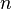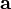Partiendo de un escalar n , y de un vector mathbf{a} , el producto de n , por mathbf{a} se representa 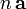n , mathbf{a} y se realiza multiplicando cada una de las componentes del vector por el escalar; esto es, dado el vector

mathbf{a} = a_x mathbf{i} + a_y mathbf{j} + a_z mathbf{k}

su producto por el escalar 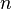n , es

n , mathbf{a} = na_x mathbf{i} + na_y mathbf{j} + na_z mathbf{k}

esto es, se multiplica por 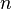n , cada una de las componentes del vector.

Producto escalar [editar]

Artículo principal: Producto escalar

Producto vectorial [editar]

Artículo principal: Producto vectorial

Derivada de un vector [editar]

Dado un vector que es función de una variable independiente

mathbf{a}(t)= a_x(t) mathbf{i} +a_y(t) mathbf{j} +a_z(t) mathbf{k}

Calculamos la derivada del vector con respecto de la variable t, calculando la derivada de cada una de sus componentes como si de escalares se tratara:

frac{d}{dt}mathbf{a}(t)= frac{d}{dt}a_x(t) mathbf{i} + frac{d}{dt}a_y(t) mathbf{j} + frac{d}{dt}a_z(t) mathbf{k}

teniendo en cuenta que los vectores unitarios son constantes en módulo y dirección.

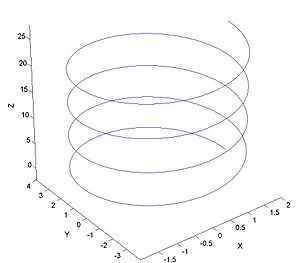
mathbf{r}(t)=sin(t) mathbf{i}+cos(t)mathbf{j}+ 5tmathbf{k}

Veamos un ejemplo de derivación de un vector, partiendo de una función vectorial:

mathbf{r}(t) = sin(t) mathbf{i} + cos(t) mathbf{j} + 5t mathbf{k}

Esta función representa una curva helicoidal alrededor del eje z, de radio unidad, como se ilustra en la figura. Podemos imaginar que esta curva es la trayectoria de una partícula y la función 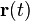mathbf r (t), representa el vector de posición en función del tiempo t. Derivando tendremos:

frac{dmathbf{r}(t)}{dt} = frac{d}{dt}sin(t) mathbf{i} + frac{d}{dt}cos(t) mathbf{j} + frac{d}{dt}5t mathbf{k}

Realizando la derivada:

frac{dmathbf{r}(t)}{dt} = cos(t) mathbf{i} - sin (t) mathbf{j} + 5 mathbf{k}

La derivada del vector de posición respecto al tiempo es la velocidad, así que esta segunda función determina el vector velocidad de la partícula en función del tiempo, podemos escribir:

mathbf{v}(t) = cos(t) mathbf{i} - sin(t) mathbf{j} + 5 mathbf{k}

Este vector velocidad es un vector tangente a la trayectoria en el punto ocupado por la partícula en cada instante. Si derivásemos de nuevo obtendríamos el vector aceleración.

Ángulo entre dos vectores [editar]

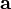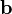El ángulo determinado por las direcciones de dos vectores mathbf{a} y mathbf{b} viene dado por:

cos theta = frac {mathbf a cdot mathbf b}{|mathbf{a}| , |mathbf{b}|}

Requerimientos físicos de las magnitudes vectoriales [editar]

No cualquier n-tupla de funciones o números reales constituye un vector físico. Para que una n-tupla represente un vector físico, los valores numéricos de las componentes del mismo medidos por diferentes observadores deben transformarse de acuerdo con ciertas relaciones fijas.

En mecánica newtoniana generalmente se utilizan vectores genuinos, llamados a veces vectores polares, junto con pseudovectores, llamados vectores axiales que realmente representan el dual de Hodge de magnitudes tensoriales antisimétricas. El momento angular, el campo magnético y todas las magnitudes que en cuya definición interviene el producto vectorial son en realidad pseudovectores o vectores axiales.

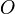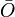En teoría especial de la relatividad, sólo los vectores tetradimensionales cuyas medidas tomadas por diferentes observadores pueden ser relacionadas mediante alguna transformación de Lorentz constituyen auténticas magnitudes vectoriales. Así las componentes de dos magnitudes vectoriales medidas por dos observadores O, y bar{O} deben relacionarse de acuerdo con la siguiente relación:

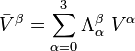
bar{V}^beta = sum_{alpha=0}^3 Lambda_alpha^beta V^alpha


Donde 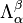Lambda_alpha^beta son las componentes de la matriz que da la transformación de Lorentz. Magnitudes como el momento angular, el campo eléctrico o el campo magnético o el de hecho en teoría de la relatividad no son magnitudes vectoriales sino tensoriales.

Referencia [editar]

Bibliografía [editar]

  • Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes) (en español). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
  • Resnick,Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons.
  • Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6ª edición (en inglés), Brooks/Cole. ISBN 0-534-40842-7.
  • Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes) (en español). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.

Enlaces externos [editar]

Obtenido de "http://es.wikipedia.org/wiki/Vector_(f%C3%ADsica)"

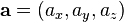
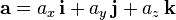
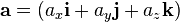
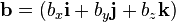
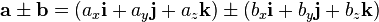
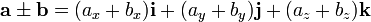
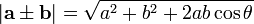
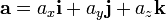
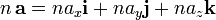
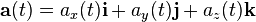
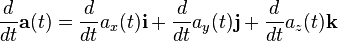
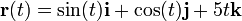
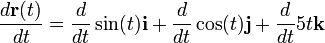
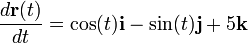
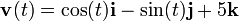
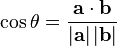
0 comentarios